Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
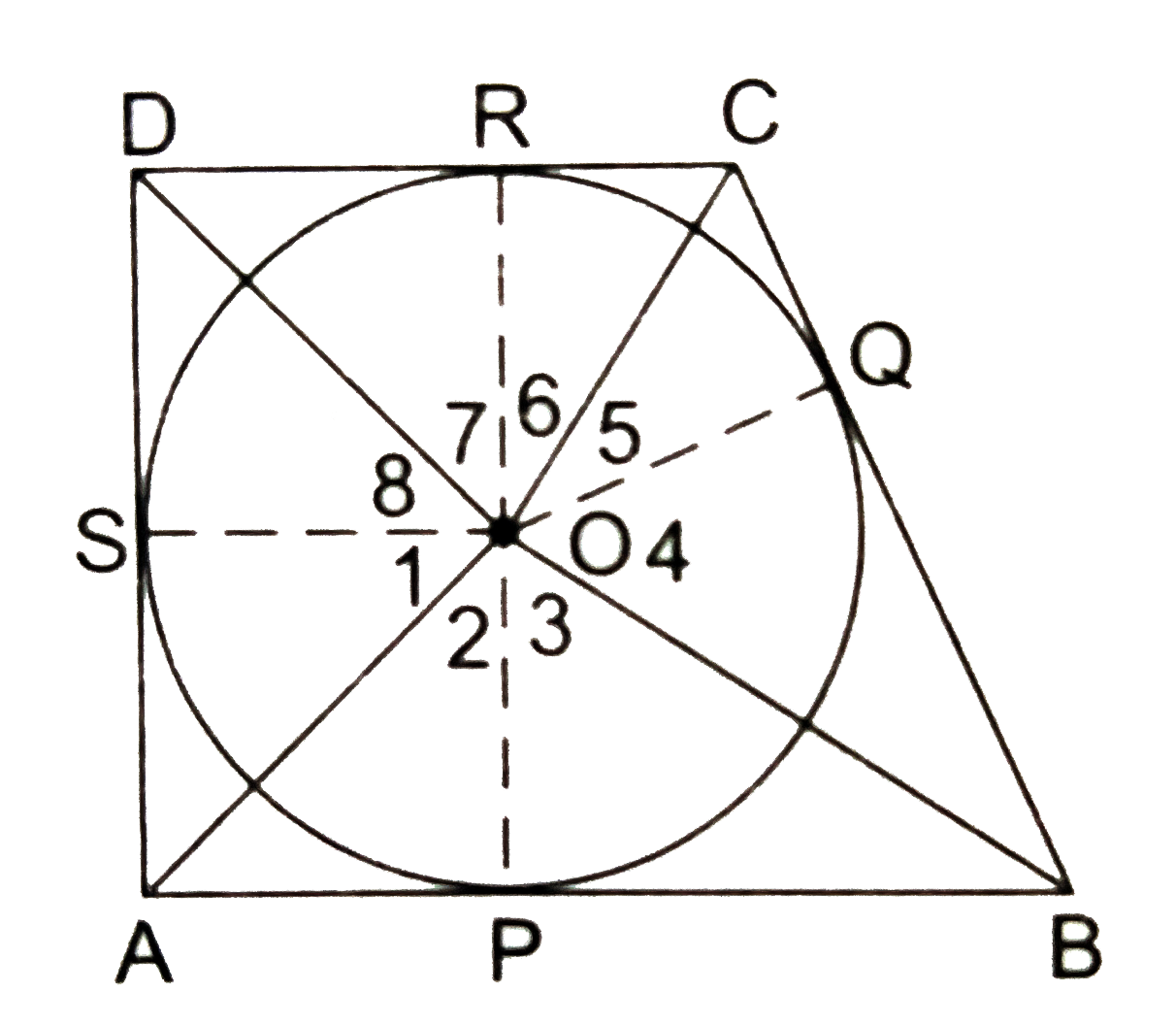
GIVEN A quad. ABCD circumscribes a circle with centre O.
TO PROVE ∠AOB+∠COD=180∘
and ∠AOD+∠BOC=180∘.
CONSTRUCTION Join OP, OQ, OR and OS
PROOF We know that the tangents drawn from an external point of a circle subtend equal angles at the centre.
∴∠1=∠2,∠3=∠4, ∠5=∠6 and ∠7=∠8
And, ∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=360∘ [at a point]
⇒2(∠2+∠3)+2(∠6+∠7)=360∘, and
2(∠1+∠8)+2(∠4+∠5)=360∘
⇒∠2+∠3+∠6+∠7=180∘ and ∠1+∠8+∠4+∠5=180∘
⇒∠AOB+∠COD=180∘ and ∠AOD+∠BOC=180∘
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Prove that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionState and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionIf a Quardlateral is circumscribed of a circle and ∠AOB is 135∘ find angle COD . O is the centre of circle
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionProve that the rectangle circumscribing a circle is a square
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionProve that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
View Solution
