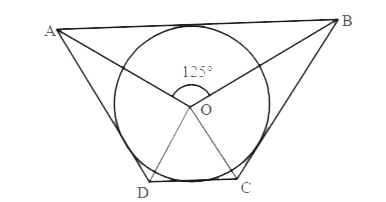
If a Quardlateral is circumscribed of a circle and ∠AOB is 135∘ find angle COD . O is the centre of circle
The correct Answer is:45∘
To solve the problem, we need to find the angle ∠COD given that ∠AOB=135∘ and that the quadrilateral ABCD is circumscribed about a circle.
1. Understanding the Properties of the Quadrilateral:
A quadrilateral that can be circumscribed about a circle has a special property: the sum of the angles subtended by opposite sides at the center of the circle is equal to 180∘. This means:
∠AOB+∠COD=180∘
2. Substituting the Given Angle:
We know that ∠AOB=135∘. We can substitute this value into the equation:
135∘+∠COD=180∘
3. Isolating ∠COD:
To find ∠COD, we need to isolate it on one side of the equation. We can do this by subtracting 135∘ from both sides:
∠COD=180∘−135∘
4. Calculating ∠COD:
Now, we perform the subtraction:
∠COD=45∘
Thus, the measure of angle COD is 45∘.
Final Answer:
∠COD=45∘
A quadrilateral that can be circumscribed about a circle has a special property: the sum of the angles subtended by opposite sides at the center of the circle is equal to 180∘. This means:
∠AOB+∠COD=180∘
We know that ∠AOB=135∘. We can substitute this value into the equation:
135∘+∠COD=180∘
To find ∠COD, we need to isolate it on one side of the equation. We can do this by subtracting 135∘ from both sides:
∠COD=180∘−135∘
Now, we perform the subtraction:
∠COD=45∘
∠COD=45∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the angle ∠AED if O is the centre of the circle?
 A90∘B45∘C120∘DNone of these
A90∘B45∘C120∘DNone of theseIf O is the centre of circle and ∠ADE=60∘ then find ∠AOC
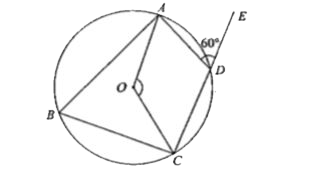 A60∘B100∘C120∘DNone of these
A60∘B100∘C120∘DNone of theseO is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘
Prove that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionIn the figure, AB is the diameter of the circle. If ∠AOC=135∘ then find the ∠CDB.
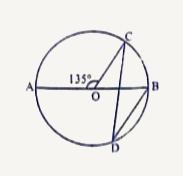
View Solution‘O’ is the centre of the circle. Find ∠(ADB)
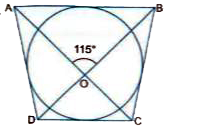
View SolutionIn Fig the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB=115∘, then find ∠AOB=115∘ then find ∠COD.
View Solution