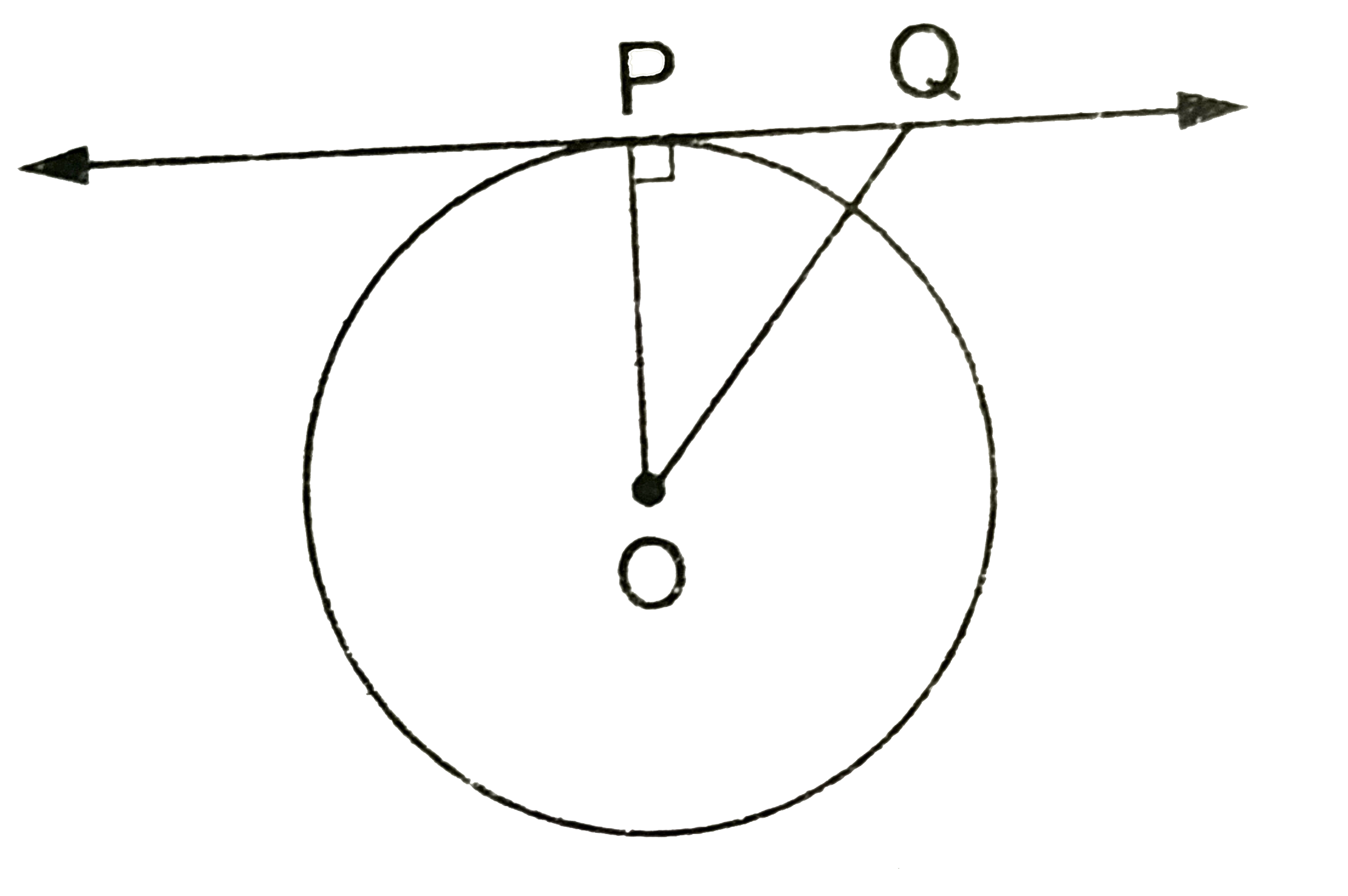
PQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
30∘
45∘
60∘
90∘
We have OP⊥PQ, i.e., ∠OPQ=90∘
ΔOPQ is isosceles ⇒OP=PQ⇒∠OQP=∠POQ=45∘
[∵ in a triangle, angles opposite equal sides are equal].
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple-choice questions (MCQ)39videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason1videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
PQ is a tangent to a circle with centre O at the point P . If OPQ is an isosceles triangle, then ∠OQP is equal to 30o (b) 45o (c) 60o (d) 90o
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.View Solution
Knowledge Check
- Question 1 - Select One
AB and AC are tangents to the circle with centre O. Then x equals.
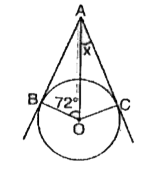 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘ - Question 2 - Select One
If tangent PA and PB from a point P to a circle with centre O are inclined to each other at angle 80∘, then ∠POA is equal to
A50∘B60∘C70∘D80∘ - Question 3 - Select One
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70∘, then ∠POA is equal to
A70∘B55∘C100∘D40∘
In figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
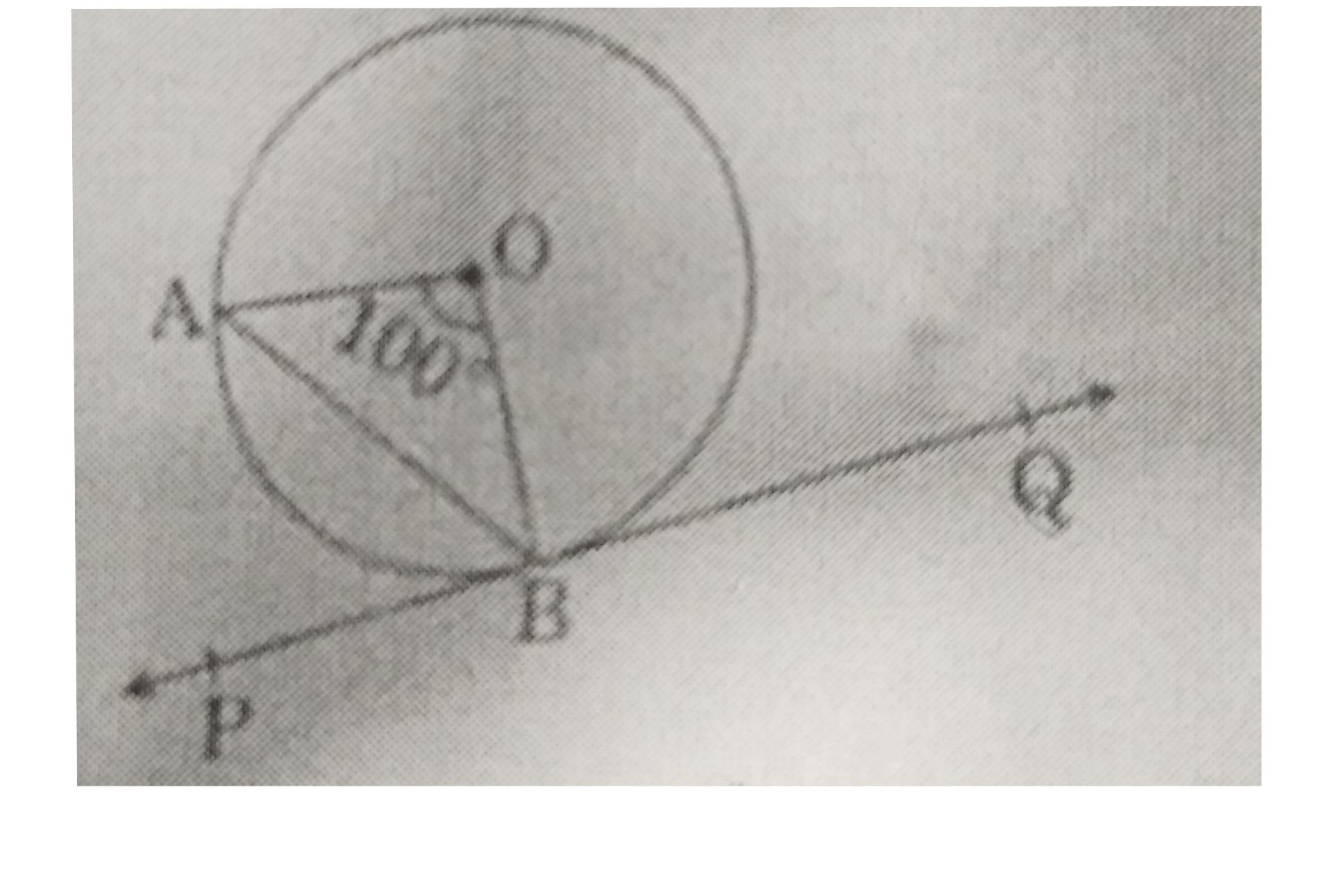 View Solution
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to
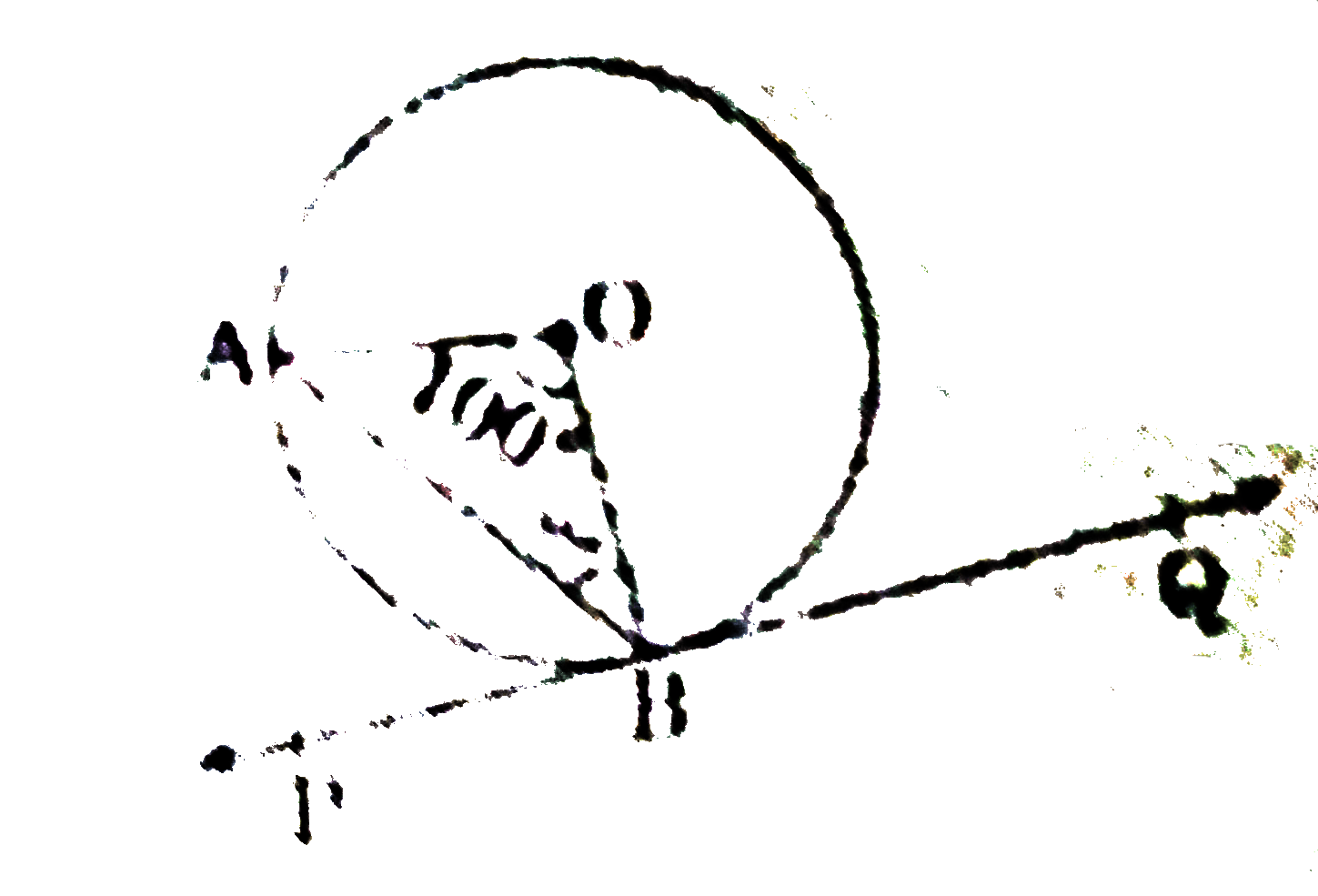 View Solution
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
View Solution

