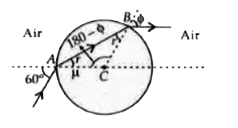
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

μ=√2
μ=√32
μ=√3
μ=√52
The correct Answer is:A
Apply Snell.s law at points A abd B
1sin60∘=μsinr …(i)
μsinr=1sinϕ ...(ii)
Solving equations (i) and (ii), we get ϕ=60∘
Also, 2r+180∘−ϕ=180∘
2r+180∘−60∘=180∘
or 2r=60∘ or r=30∘
From equation (i), we get μ=sin60∘sinr=sin60∘sin30∘=√3
Topper's Solved these Questions
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - Check your NEET vitals
25 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

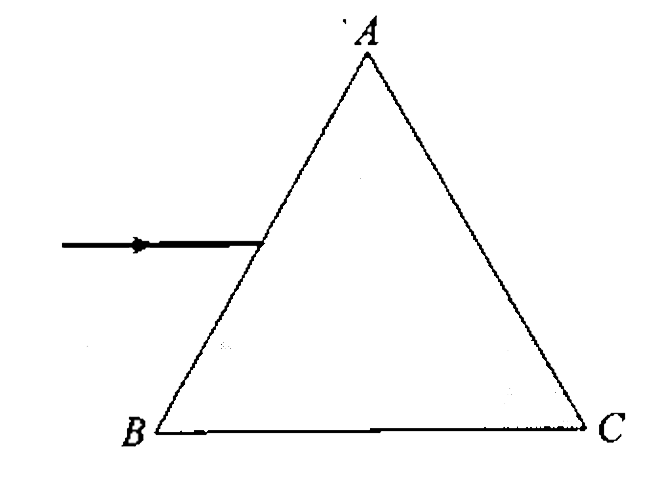
View SolutionA ray of light is incident on an equilateral triangular prism parallel to its base as shown in the figure. The ray just fails to emerge from the face AC. If μ be the refractive index of the prism then the relation(s) is/are :
View Solution
Knowledge Check
A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
A32B53C2D52A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
A32B53C2D52A poing source of light at the surface of a sphere causes a paralel beam of light to emerge from the opposite surface of the sphere. The refractive index of the material of the sphere is
A1.5B5/3C2D2.5
A ray of light is incident horizontally on the face AB of the.right angled prism as shown in the figure. If the ray emerges grazing the surface AC, find the value of ϕ. Refractive index of the material of the prism is given to be n.
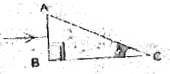
View SolutionParallel rays are incident on a transparent sphere along its one diameter. After refraction, these rays converge at the other end of this diameter. The refractive index for the material of sphere is
View SolutionA ray of light incident on a transparent sphere at an angle π/4 and refracted at an angle r, emerges from the sphere after suffering one internal reflection. The total angle of deviation of the ray is
View SolutionA point source of light is kept on the surface of a sphere and it is found that parallel light rays emerge from the other side of the sphere. What is refractive index of material of the sphere ?
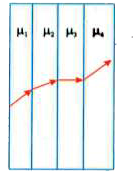
View SolutionA ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav
View Solution
