Two solid spherical planets have equal radii and mass of 4M and 9M and distance between their centre is 6R. A body of mass m is projected toward heavy planet, then what should be the ditsance of body of mass m from lighter planet so that the gravitational force on it will be zero ?Solution in Gujrati
The correct Answer is:r = 2.4 R from planet of mass 4M
Step by step video, text & image solution for Two solid spherical planets have equal radii and mass of 4M and 9M and distance between their centre is 6R. A body of mass m is projected toward heavy planet, then what should be the ditsance of body of mass m from lighter planet so that the gravitational force on it will be zero ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - B Numerical From Textual Exercise (Answer the following:)
21 Videos
- GRAVITATIONBOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - B ADDITIONAL EXERCISE
4 Videos
- GRAVITATIONBOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - A Try Yourself (VSQs)
76 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D
1 Videos
Similar Questions
You can shled a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
View SolutionAs you have learnt in the text a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth's gravity at the site of this satellite ? (Take the potential energy at infinity to be zero).
Mass of the earth 6.0×1024(kg) ,
Radius = 6400 km .
View SolutionDescribe Ptolemy model for planetary motion.
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA small body of mass is projected with a velocity just sufficient to make it reach from the surface of a planet ( or radius 2R and mass 3M) to the surface of another planet (or radius R and mass M). The distance between the centres of the two spherical planets is 6R. the distance of the body from the centre of bigger planet is 'x' at any moment. During the journey, find the distance 'x' where the speed of the body is (a) maximum (b) minimum. Assume motion of body along the line joining centres of planets.
View SolutionTwo solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
View SolutionM और 16 M द्रव्यमान के दो ग्रह 10a दुरी पर स्थित हैं। उनकी त्रिज्याएँ क्रमशः a और 2a हैं। दीर्घ ग्रह से m द्रव्यमान के एक पिंड को किस न्यूनतम वेग से दागा जाये कि वह लघु ग्रह तक जा सके ?
View SolutionWith what speed v0 should a body be projected as shown in the figure, with respect to a planet of mass M so that it would just be able to graze the planet and escape ? The radius of the planet is R. (Assume that the planet is fixed ).
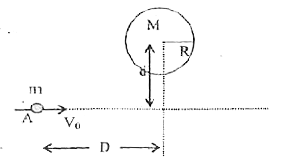
View SolutionTwo planets of mass M and 16M of radius a and 2a respectively, are at distance 10a . Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionThe masses of two planets are M and 16M respectively. Their radii are a and 2a respectively and their centres are 10 a apart. A body of mass m is fired straight from the surface of the larger planet towards the smaller planet. What should be the minimum projectile speed so that it reaches the surface of the smaller planet ? Obtain the expression in terms of G, M and a.
View Solution
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionTwo solid spherical planets of equal radii R have masses 4M and 9M. Their centres are scparated by a distance 6R. A projectile of mass m is sent from the planet of mass 4M towards the heavier planet. If the distance r of the point from the lighter planet where the gravitational 'force on the projectile is zero is kR, then calculate k.
View SolutionEscape velocity of a body of 1 g mass on a planet is 100 m/sec . Gravitational Potential energy of the body at the planet is
View Solution
