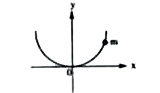
A bead of mass (m) is located on a parabolic wire with its axis vertical and vertex at the origin is shown in figure and whose equation x2=4ay. The wire frame is fixed and the bead can slide on it without friction. The bead is released from the point y = 4a on the wire frame from rest. The tangential accelera tion of the bead when it reacher the position given by y=a is
 Solution in Telugu
Solution in Telugu
g2
√3g2
g√2
g√5
The correct Answer is:C
Step by step video & image solution for A bead of mass (m) is located on a parabolic wire with its axis vertical and vertex at the origin is shown in figure and whose equation x^(2)= 4ay. The wire frame is fixed and the bead can slide on it without friction. The bead is released from the point y = 4a on the wire frame from rest. The tangential accelera tion of the bead when it reacher the position given by y=a is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)3videos
HORIZONTAL CIRCULAR MOTION
- BOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) Integer Type Questions)1videos
HORIZONTAL CIRCULAR MOTION
- BOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3154videos
GRAVITATIONAL
- BOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer Type Questions)12videos
KINEMATICS
Similar Questions
A vehicle whose wheel track is 1.7m wide and whose centre of gravity 1 m above the road and central between the wheels, taken a curve whose radius 50m, on a level road. The speed at which the inner wheel would leave the road is close to n×5m/s.
01:48View SolutionA solid body starts rotating about a stationary axis with an angular acceleration β = at where a=2×10−2rad/sec2 How soon from beginning of rotation will be total acceleration vector of an arbitrary point of the body form an angle α=60∘ with its velocity vector
05:41View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
02:26View SolutionThree particles start from origin at the same time: one with velocity v1 along positive x - axis, the second along the positive y-axis with a velocity v2 and the third along the line y=x with such a speed that all the three always stay in a straight line, then the velocity of the third particle is √kV1V2(V1+V2).
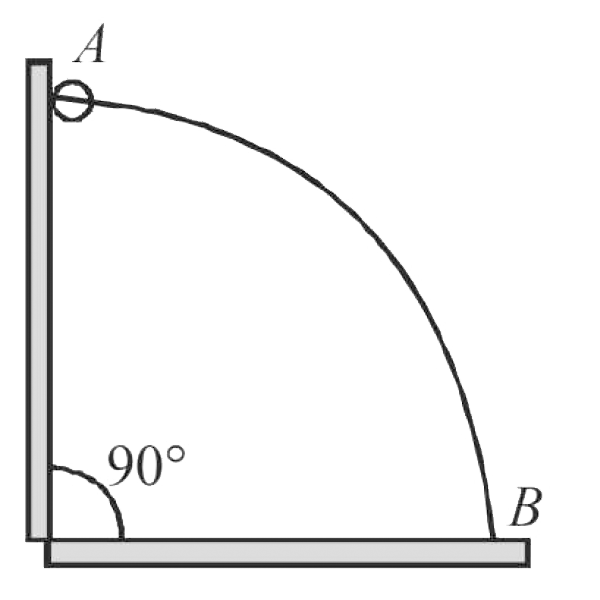
01:51View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA piece of wire is bent in the shape of a parabola y = Kx^(2) (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
03:22View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
 04:52View Solution
04:52View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
03:54View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 07:35View Solution
07:35View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the verticle line is
03:21View SolutionA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the vertical line is
03:21View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
04:59View Solutionएक तार जो एक छोटे मोती के मध्य में स्थित छिद्र से गुजरता है, को एक चतुर्थाशा वृत्त के अनुरूप मोड़ा गया है। तार को भूमि पर उर्ध्व तल में स्थित किया गया है, जैसा चित्र में दर्शाया गया है । मोती को तार के ऊपरी सिरे से छोड़ा जाता है, जिससे यह तार के अनुदिश, बिना किसी घर्षण के सरकता है। जब मोती A से B तक सरकता है। तब इसके द्वारा तार पर लगने वाला बल है:
 05:40View Solution
05:40View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the verticle line is
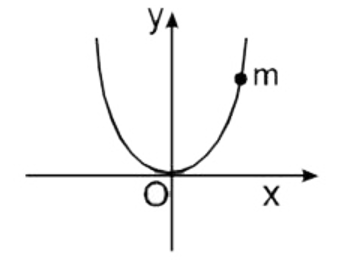
04:04View Solutionचित्रानुसार परवलय की समीकरण x2=4 ay है । इसकी ऊर्ध्वाधर अक्ष तथा शीर्ष मूल बिंदु पर है, इस परवलय तार पर m द्रव्यमान की मनका स्थित है। तार का फ्रेम स्थिर एवं ऊर्ध्वाधर तल में है तथा मनका (मनका) बिना घर्षण के परवलय पर फिसल सकता है। तार फ्रेम पर y=4a बिंदु से मनका स्थिरावस्था से छोड़ा जाता है। जब मनका y=a स्थिति पर पहुंचता है तो इसका स्पर्शरेखीय त्वरण है:
 04:16View Solution
04:16View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
 03:10View Solution
03:10View Solution
