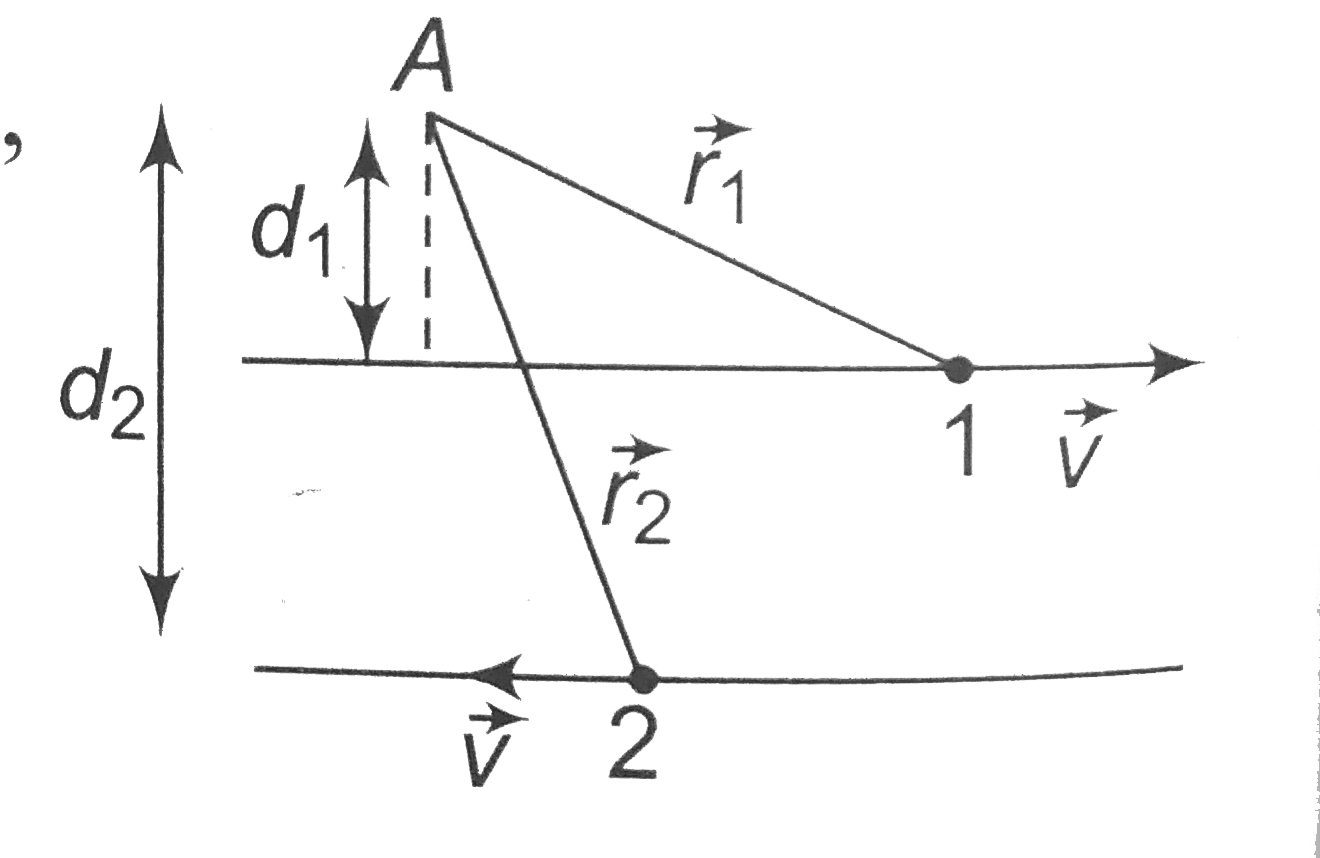
Figure shows two identical particles $1$ and $2$ , each of mass $m$ , moving in opposite directions with same speed $\to V$ along parallel lines. At a particular instant, ${\to r}_{1}$ and ${\to r}_{2}$ are their respective position vectors drawn from point $A$ which is in the plane of the parallel lines. Which of the following is the correct statement ?
.

A

Agular momentum $I_{1}$ of particle a about A is $I = m v (d_{1}) ⊙$

B

Angular momentum $I_{2}$ of particle 2 about A is $I_{2} = m v r_{2} ⊙$

C

total angular momentum of the system about A is $I = m v (r_{1} + r_{2}) ⊙$

D

total angular momentum of the system about A is $I = m v (d_{2} - d_{1}) \otimes$

Text Solution

Verified by Experts

The correct Answer is:a,b

the angular momentum L of a particle with respect toorigin is deined to be $L = r \times p$ where , r is the podsition vector of the particle and p is the linear momentum , The direction of L is is perpendicular to both d r and p by right hand rule .
For particle 1. $I_{1} = r_{1} \times m v$ is not of plane of the paper and perpendicular to $r_{1}$ and p(mv) Similarly $I_{2} = r_{2} \times m (- v)$ is into the plane of the paper and perpendicular to $r_{2} and - p$
Hence , total angular momentum
$l = l_{1} + l_{2} = r_{1} \times m v + (- r_{2} \times m v)$
$| l | = m v d_{1} - m v d_{2} a s d_{2} > d_{1}$ total angular momentum will be inward
Hence $I = m v (d_{2} - d_{1}) \otimes$
note : in the expression of angular momentum $I = r \times p$ the direction of l is taken by right hand rule .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $\to a and \to b$ be the position vectors of A and B respectively. If C is the point $3 \to a - 2 \to b$ , then which one of the following is correct?
AC is in between A and B
BA is in between C and B
CB is in between A and C
DA, B, C are not collinear
Question 2 - Select One
Let $\to a and \to b$ be the position vectors of A and B respectively. If C is the point $3 \to a - 2 \to b$ , then which one of the following is correct?
AA. C is in between A and B
BB. A is in between C and B
CC. B is in between A and C
DD. A, B and C are not collinear
Question 3 - Select One
Let $\to v_{1}, \to v_{2}, \to v_{3}, \to v_{4}$ be unit vectors in the xy-plane, one each in the interior of the four quadrants. Which of the following statements is necessarily ture. ?
A $\to v_{1} + \to v_{2} + \to v_{3} + \to v_{4} = 0$
BThere exist i, j with $1 \leq i < j \leq 4$ such $\to v_{i} + \to v_{j}$ is in the first quadrant
CThere exits i, j with $1 \leq i < j \leq 4$ such that $\to v_{i} \cdot \to v_{j} < 0$
DThere exits i, j with $1 \leq i < j \leq 4$ such that $\to v_{i} \cdot \to v_{j} > 0$

NCERT EXEMPLAR ENGLISH-SYSTEM OF PARTICLES AND ROTATIONAL MOTION -Long answer type questions

Home
Ask Doubt
Profile