Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is
simple harmonic motion
non-periodic motion
periodic motion
periodic but not SHM
To solve the question regarding the motion of a ball bearing inside a smooth curved bowl when released from a point slightly above the lower point, we will analyze the motion step by step.
1. Understanding the System:
- We have a ball bearing inside a smooth curved bowl. When the ball is released from a height slightly above the lowest point of the bowl, it will start to move under the influence of gravity.
2. Identifying Forces:
- The gravitational force acting on the ball bearing can be resolved into two components: one acting along the direction of motion (tangential) and the other acting perpendicular to the motion (normal). The tangential force is responsible for the acceleration of the ball.
3. Setting Up the Equation of Motion:
- Let’s denote the angle between the vertical and the line connecting the center of the bowl to the ball as θ. The tangential force acting on the ball is given by F=mgsin(θ).
- According to Newton's second law, F=ma, where a is the acceleration of the ball. Thus, we have:
ma=mgsin(θ)
- Dividing both sides by m gives:
a=gsin(θ)
4. Relating Angle to Displacement:
- The angle θ can be related to the displacement x from the lowest point of the bowl. For small angles, we can use the small angle approximation where sin(θ)≈xR (R is the radius of curvature of the bowl).
- Substituting this into the acceleration equation gives:
a=gxR
5. Formulating the Equation of Motion:
- The acceleration a can also be expressed as the second derivative of displacement with respect to time:
a=d2xdt2
- Thus, we have:
d2xdt2=−gRx
- The negative sign indicates that the acceleration is directed opposite to the displacement, which is characteristic of simple harmonic motion (SHM).
6. Identifying the Type of Motion:
- The equation d2xdt2=−gRx is the standard form of SHM. Therefore, the motion of the ball bearing is simple harmonic motion.
7. Calculating the Time Period:
- The angular frequency ω for SHM is given by:
ω=√gR
- The time period T of the motion can be calculated using:
T=2π√Rg
- This confirms that the motion is periodic.
Conclusion:
The motion of the ball bearing inside the smooth curved bowl, when released from a point slightly above the lower point, is simple harmonic motion (SHM) and is periodic.
- We have a ball bearing inside a smooth curved bowl. When the ball is released from a height slightly above the lowest point of the bowl, it will start to move under the influence of gravity.
- The gravitational force acting on the ball bearing can be resolved into two components: one acting along the direction of motion (tangential) and the other acting perpendicular to the motion (normal). The tangential force is responsible for the acceleration of the ball.
- Let’s denote the angle between the vertical and the line connecting the center of the bowl to the ball as θ. The tangential force acting on the ball is given by F=mgsin(θ).
- According to Newton's second law, F=ma, where a is the acceleration of the ball. Thus, we have:
ma=mgsin(θ)
- Dividing both sides by m gives:
a=gsin(θ)
- The angle θ can be related to the displacement x from the lowest point of the bowl. For small angles, we can use the small angle approximation where sin(θ)≈xR (R is the radius of curvature of the bowl).
- Substituting this into the acceleration equation gives:
a=gxR
- The acceleration a can also be expressed as the second derivative of displacement with respect to time:
a=d2xdt2
- Thus, we have:
d2xdt2=−gRx
- The negative sign indicates that the acceleration is directed opposite to the displacement, which is characteristic of simple harmonic motion (SHM).
- The equation d2xdt2=−gRx is the standard form of SHM. Therefore, the motion of the ball bearing is simple harmonic motion.
- The angular frequency ω for SHM is given by:
ω=√gR
- The time period T of the motion can be calculated using:
T=2π√Rg
- This confirms that the motion is periodic.
The motion of the ball bearing inside the smooth curved bowl, when released from a point slightly above the lower point, is simple harmonic motion (SHM) and is periodic.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position.
View SolutionWhich of the following examples represents (nearby) shm and which represents periodic but not shm.
(i) The rotation of earth about its axis.
(ii) Motion of an oscillating mercury column in a U-tube.
(iii) Motion of a ball bearing inside a smooth curved bowl when released from a point slightly above the lowermost position.
(iv) General vibration of a polyatomic molecules about its equilibrium configuration.
View SolutionThe graph as shown in. below descrines the motion of a ball rebounding from a horizontal surface being released from a point above the surface. Assume that the ball colledes each time with the floor inelastically. The quantity represented on the y-axis in the is the balls (take upward direction as positive)
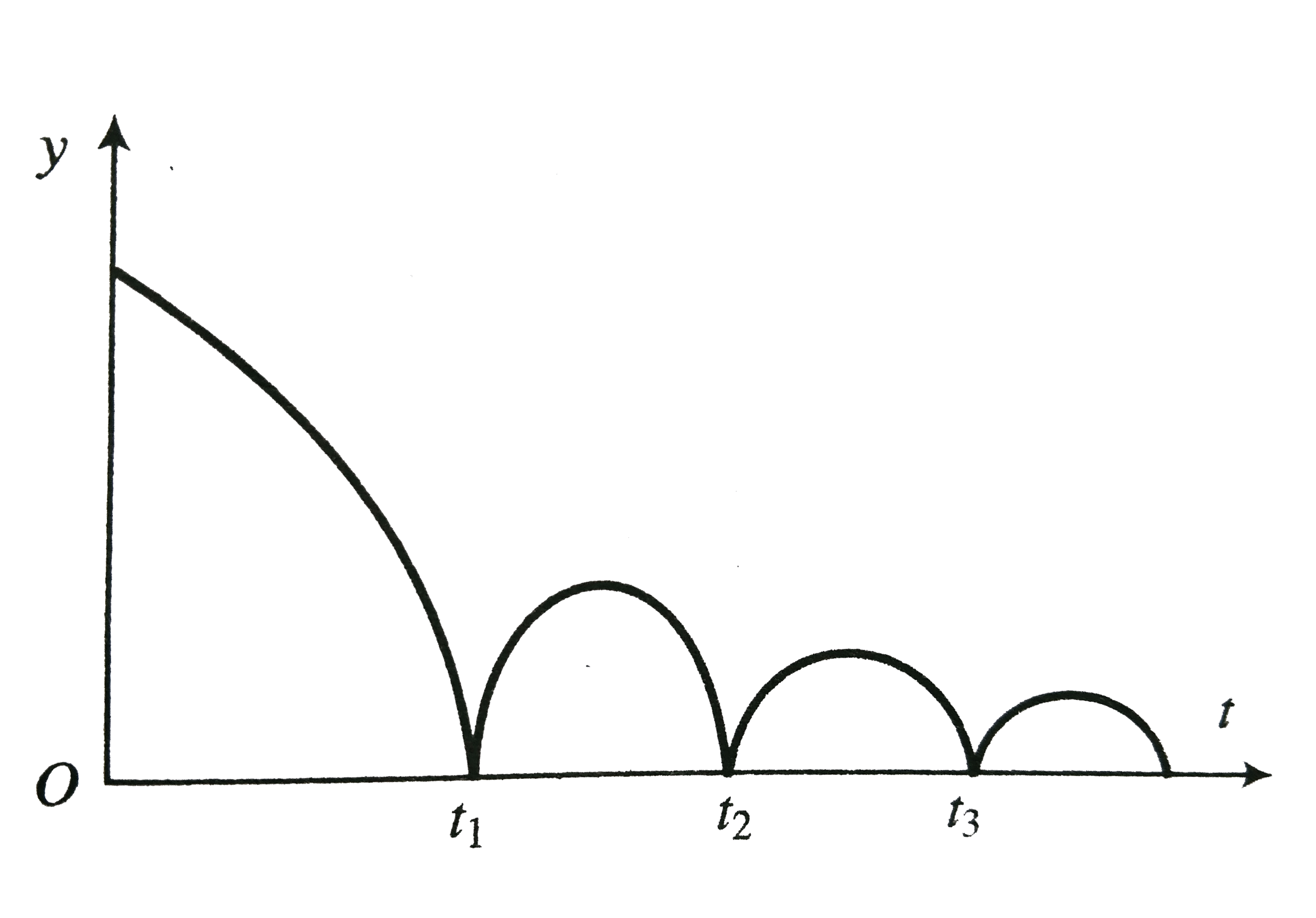 .
.
View SolutionTwo pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionFind the time taken for the ball to strike the ground . If a ball is thrown straight upwards with a speed v from a point h meters above the ground .
View SolutionA block slides down a smooth inclined placne when released from the top, while another falls freely from the same point. Which of the following is/are correct ?
View SolutionA ball of mass 1kg is suspended by an inextensible string 1m long attached to a point O of a smooth horizontal bar resting on fixed smooth supports A and B. The ball is released from rest from the position when the string makes an angle 30∘ with the vertical. The mass of the bar is 4kg. The displacement of bar when ball reaches the other extreme position (in m) is

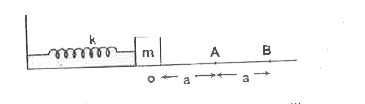
View SolutionIn the shown figure, mass m rests on smooth horizontal surface, connected with an ideal spring. If mass is displaced to the point A and released from rest, it reaches the point O in time t0.
Now the block is displaced to the point B and released from rest. How much time it will take in travelling from point A to point O.
View SolutionA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)

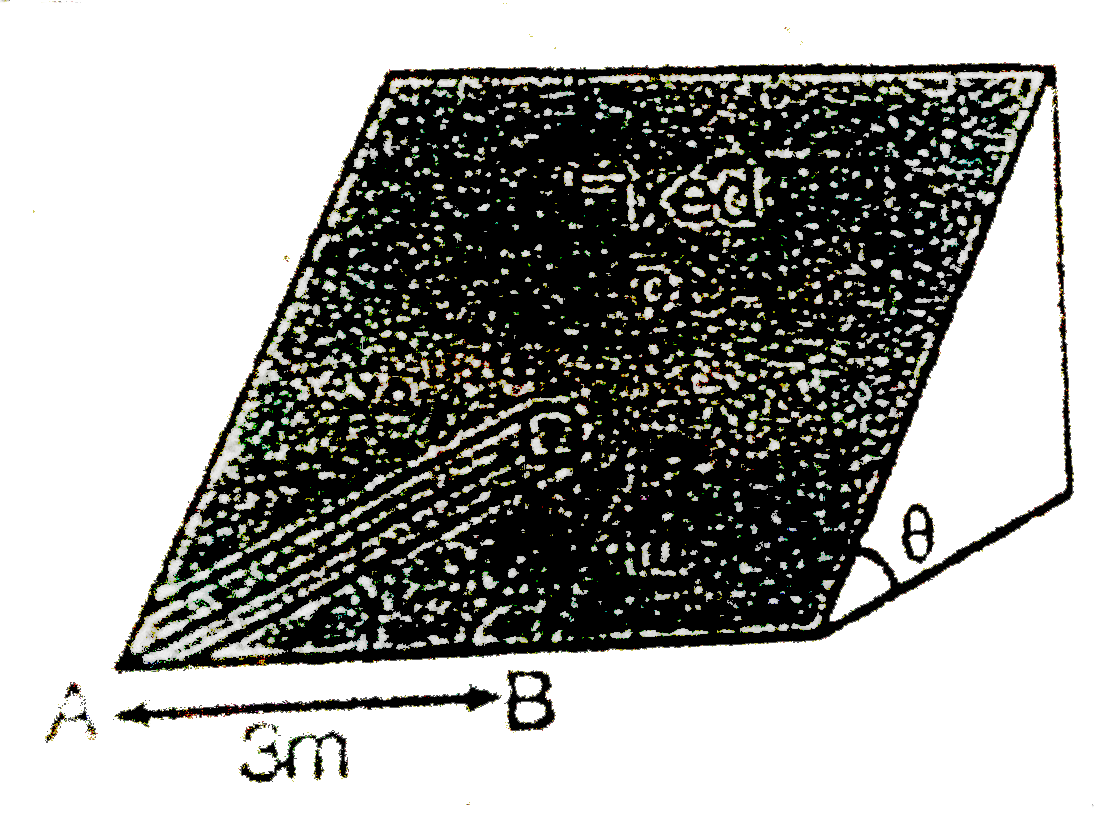
View SolutionThere is inclined surface of inclination θ=30∘. A smooth groove is cut into it forming angle α with AB. A steel ball is free to slide along the groove. If the ball is released from the point O at top end of the groove, the speed when it comes to A is [g=10m/s2]
View Solution
