If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form Option1: a square Option2: a rhombus Option3: a rectangle Option4: any other parallelogram
a square
a rhombus
a rectangle
any other parallelogram
The correct Answer is:C
To solve the problem, we need to analyze the given information about the angles formed by the two parallel lines APB and CQD, and how their angle bisectors interact.
1. Identify the Angles:
We have two parallel lines, APB and CQD. The angles we are interested in are APQ, BPQ, CQP, and PQD.
2. Use Properties of Parallel Lines:
Since APB and CQD are parallel, we know that:
- Angle APQ is equal to angle PQD (alternate interior angles).
- Therefore, we can write:
∠APQ=∠PQD
3. Angle Bisectors:
The angle bisectors of angles APQ and PQD will create two new angles:
- Let MPQ be the angle bisector of APQ and NQP be the angle bisector of PQD.
- Since ∠APQ=∠PQD, it follows that:
∠MPQ=∠NQP
4. Establish Parallel Lines:
Since MPQ and NQP are equal and are both angle bisectors, we can conclude that:
- MP∥QN (as they are corresponding angles).
5. Consider the Other Angles:
Similarly, we can analyze angles CQP and BPQ:
- By the same reasoning, we find that the angle bisectors of these angles will also be parallel:
PN∥MQ
6. Forming a Parallelogram:
From the above steps, we have established that:
- MP∥QN
- PN∥MQ
Thus, the figure formed by the bisectors MP,QN,PN, and MQ is a parallelogram.
7. Check for Right Angles:
To determine if this parallelogram is a rectangle or a square, we need to check if any angle is 90 degrees.
- Since angle CQD is 180 degrees, we can express it as:
∠CQP+∠DQP=180∘
- Dividing by 2 gives us:
12∠CQP+12∠DQP=90∘
- This means that the angles MQP and NQP are both 90 degrees.
8. Conclusion:
Since we have established that all angles in the quadrilateral formed by the angle bisectors are right angles, we conclude that the shape is a square.
Final Answer:
The bisectors of angles APQ, BPQ, CQP, and PQD form a square.
We have two parallel lines, APB and CQD. The angles we are interested in are APQ, BPQ, CQP, and PQD.
Since APB and CQD are parallel, we know that:
- Angle APQ is equal to angle PQD (alternate interior angles).
- Therefore, we can write:
∠APQ=∠PQD
The angle bisectors of angles APQ and PQD will create two new angles:
- Let MPQ be the angle bisector of APQ and NQP be the angle bisector of PQD.
- Since ∠APQ=∠PQD, it follows that:
∠MPQ=∠NQP
Since MPQ and NQP are equal and are both angle bisectors, we can conclude that:
- MP∥QN (as they are corresponding angles).
Similarly, we can analyze angles CQP and BPQ:
- By the same reasoning, we find that the angle bisectors of these angles will also be parallel:
PN∥MQ
From the above steps, we have established that:
- MP∥QN
- PN∥MQ
Thus, the figure formed by the bisectors MP,QN,PN, and MQ is a parallelogram.
To determine if this parallelogram is a rectangle or a square, we need to check if any angle is 90 degrees.
- Since angle CQD is 180 degrees, we can express it as:
∠CQP+∠DQP=180∘
- Dividing by 2 gives us:
12∠CQP+12∠DQP=90∘
- This means that the angles MQP and NQP are both 90 degrees.
Since we have established that all angles in the quadrilateral formed by the angle bisectors are right angles, we conclude that the shape is a square.
The bisectors of angles APQ, BPQ, CQP, and PQD form a square.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
14 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is Option1 a rhombus Option2 a rectangle Option3 a square Option4 any parallelogram
View SolutionA transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
View Solution
Knowledge Check
Lightning was discovered by option 1 ohm option 2 Thomson Option 3 Franklin Option 4 Faraday
AOhmBThomsonCFranklinDFaraday
D and E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is Option1 a square Option2 a rectangle Option3 a rhombus Option4 a parallelogram
View SolutionElectron microscope is used for
Option 1
spin
Option 2
wave nature
Option 3
negative charge
Option 4
none of these
View SolutionAssertion: If m parallel lines are intersected by n other parallel llines, then the number of parallelograms thus formed is mn(m−1)(n−1)4, Reason: A selection of 4 lines 2 from m parallel lines and 2 from n parallel lines gives one parallelogram. (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionA naked RNA particle causing the symptoms like that of a virus disease is known as
Option 1 Viroid
Option 2 Virion
Option 3 Virus
Option 4 Prion
View Solution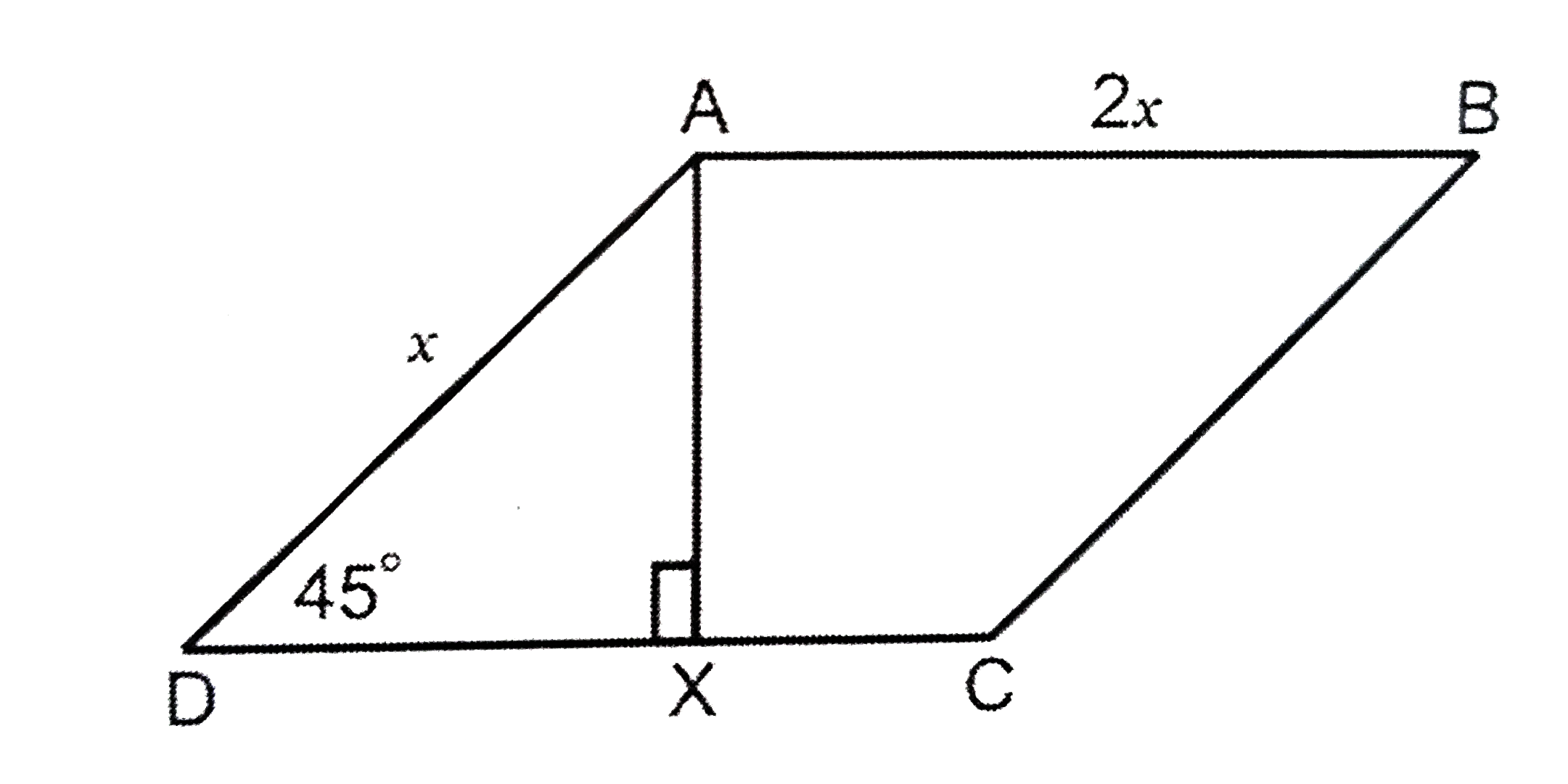
In a parallelogram, the ratio of the two adjacent sides is 1 : 2. If the area of the parallelogram is 20 square units and the angle beween the two sides is 45∘, what is the area, to the nearest integer, of the rectangle having the sides equal to that of the parallelogram?
View SolutionOption 1. 75 Option 2. 79 Option 3. 82 Option 4. 84
View SolutionTwo parallel lines l and m are intersected by a transversal p . Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View Solution
