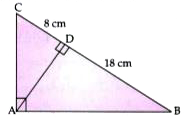
In figure, if ∠BAC=90∘ and AD⊥BC. Then,

A
BD.CD=BC2
B
AB⋅AC=BC2
C
BD⋅CD=AD2
D
AB⋅AC=AD2
Video Solution
Text Solution
The correct Answer is:C
Ib ΔADB and ΔADC,
∠d=∠D=90∘
∠DBA=∠DAC [each equal to 90∘−<C]
∴ΔADB~ΔADC [by AAAsimilarity criterion]
∴BDAD=ADCD
⇒BD⋅CD=AD2
|
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions
12 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Short Answer Type Questions
15 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
Knowledge Check
In triangle ABC, ∠BAC=90∘ and AD⊥BC Such that ∠OBA=∠DAC Then:
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
In the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
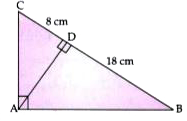
If BD = 18 cm, CD = 8 cm find AD.
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.

(i) Prove ΔADB~ΔCDA.
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
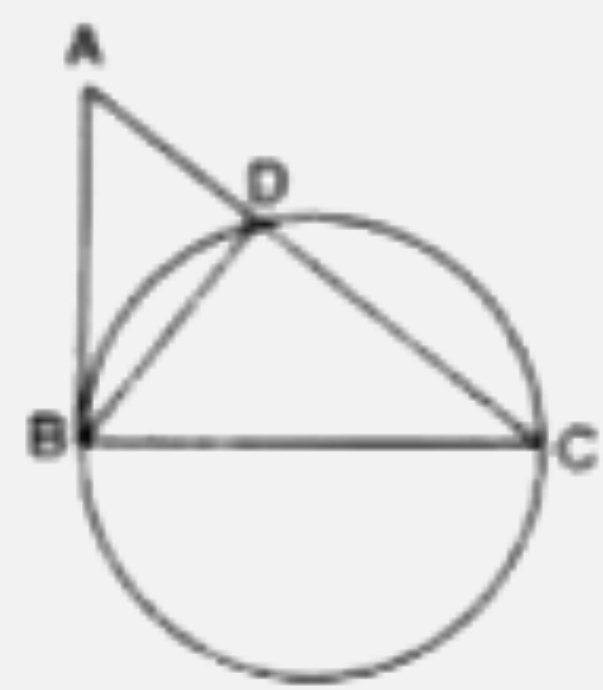
AC×AD=AB2
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:

AC×CD=BC2
View SolutionIn the following figure, ∠BAC=60∘ and ∠ABC=65∘.
Prove that :
(i) CF>AF (ii) DC>DF

View SolutionIn the given figure , ∠C=90∘ and BD = DC Find :
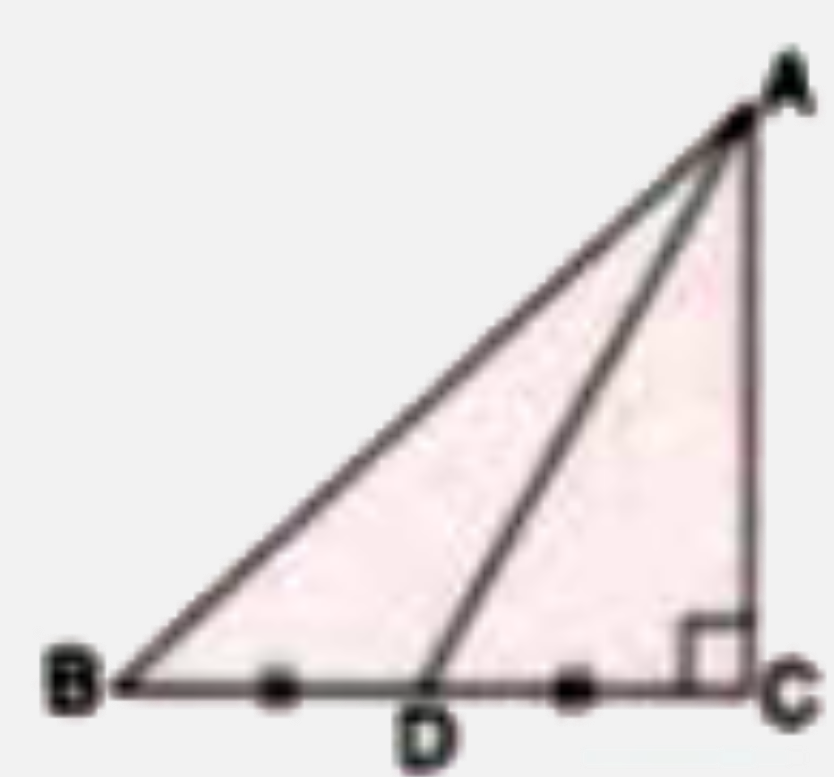
cot∠DACcot∠BAC
View SolutionIn the given figure , ∠C=90∘ and BD = DC Find :

cot∠ABCcot∠ADC
View Solution