A conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t)ˆk
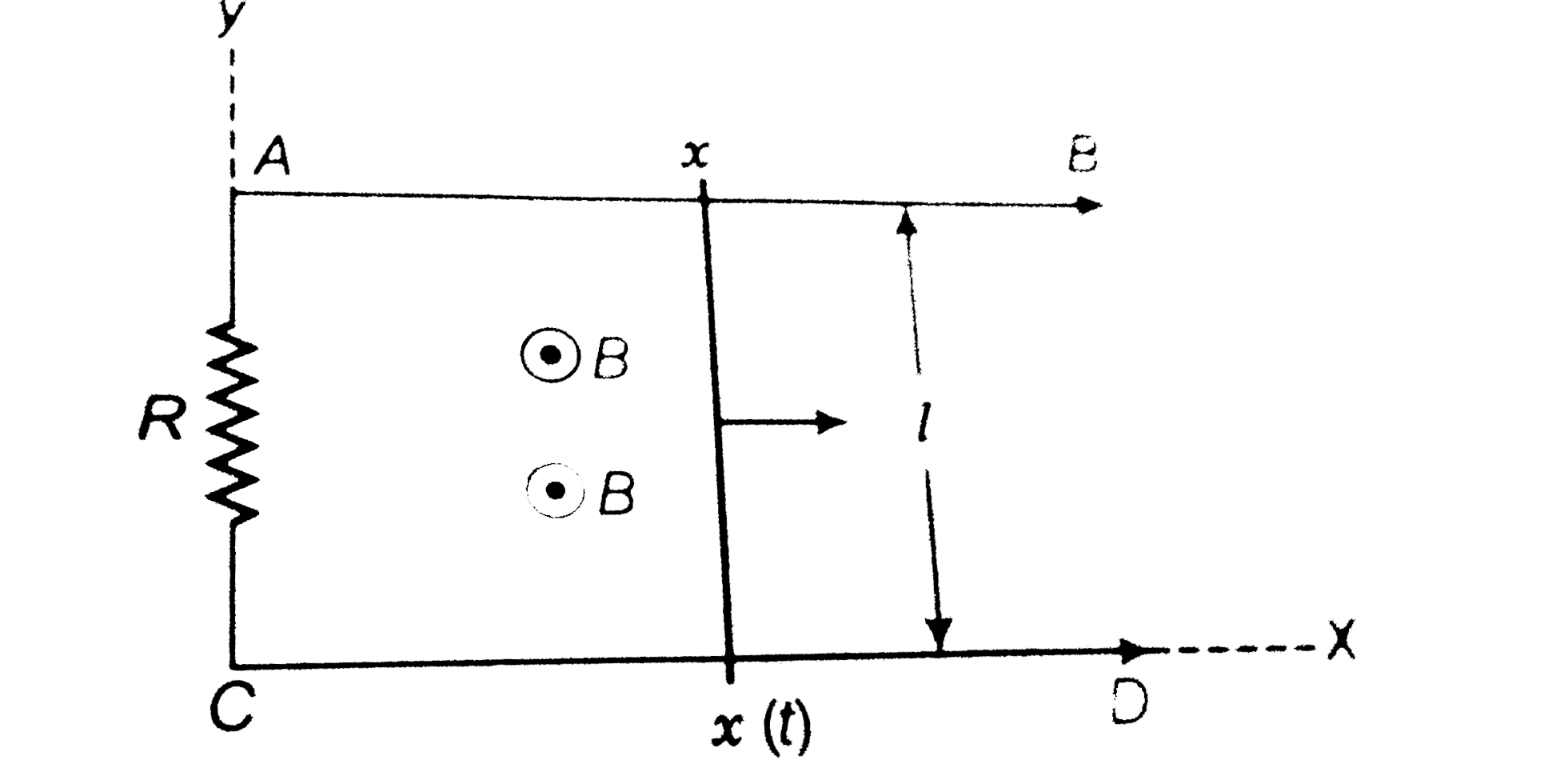
Let us assume that the parallel wiers at are y=0, i.e., along x-axis and y-l, At=0, XY has x=0 i.e., along y-axis.
(i) Let the wire be at x=x(t) at time t.
The magnetic flux linked with the loop is given by
θ=B.A=BAcos0=BA
at any instant t
Magnetic flux = B(t)(l×x(t))
Total emf in the circuit= emf due to change in field (along XYAC) + the motional emf across XY
E=−dϕdt=−(dB(t)dtlx(t)−B(t)lv(t) [second term due to motional emf]
Electric current in clockwise direction is given by
I=1RE
The force acting on the conductor is given by F=ilBsin90∘=ilB
Substituting the values, we have
Force =IB(t)R[−dB(t)dtIx(t)−B(t)Iv(t)]ˆi
Applying Newton's second law of motion,
md2xdt2=−I2B(t)RdBdtx(t)−I2B2(t)Rdxdt
Which is the required equation.
ii) If B is independent of time i.e., B=Constant
Or dBdt=0
Substituting the above value in Eq(i), we have
d2xdt2+I2B2mRdxdt=0
dvdt+I2B2mRV=0
Integrating using variable separable form of differential equation, we have
V=Aexp(−I2B2tmR)
Applying given conditions
at t=0v=u0
v(t)=u0exp(−I2B2t/mR)
This is the required equation,
Since the power consumption is given by P=I2R
Here,
I2R=B2I2V2(t)R2×R
=B2I2Ru20exp(−2I2B2tImR)
Now, energy consumed in time interval dt is given by energy consumed =Pdt=I2Rdt
Therefore, total energy consumed in time t
=∫t0I2Rdt=B2I2Rμ20mR2I2B2[1−e−(l2B2t/mr)
m2u20−m2v2(t)
= decrease in kinetic energy.
This proves that the decrease in kinetic energy of XY equals the heat lost in R.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Short answer type questions
5 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
Similar Questions
A horizontal wire is free to slide on the verticle rails of a conducting frame as shown in figure. The wire has a mass m and length l and the resistance of the circuit is R. If a uniform magnetic field B is directed perpendicular to the frame, the terminal speed of the wire as it falls under the force of gravity is

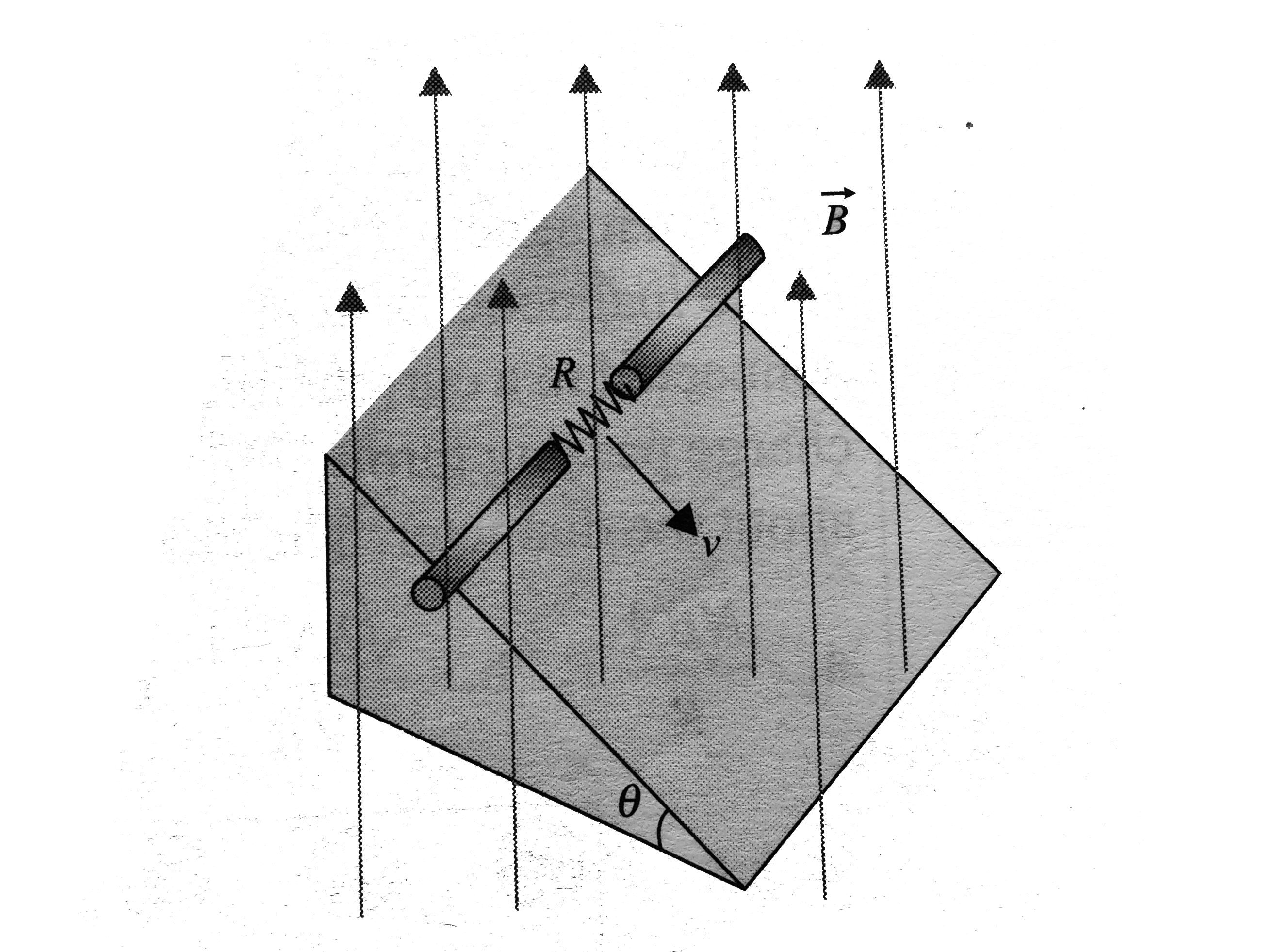
View SolutionA wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View Solution
Knowledge Check
A conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.
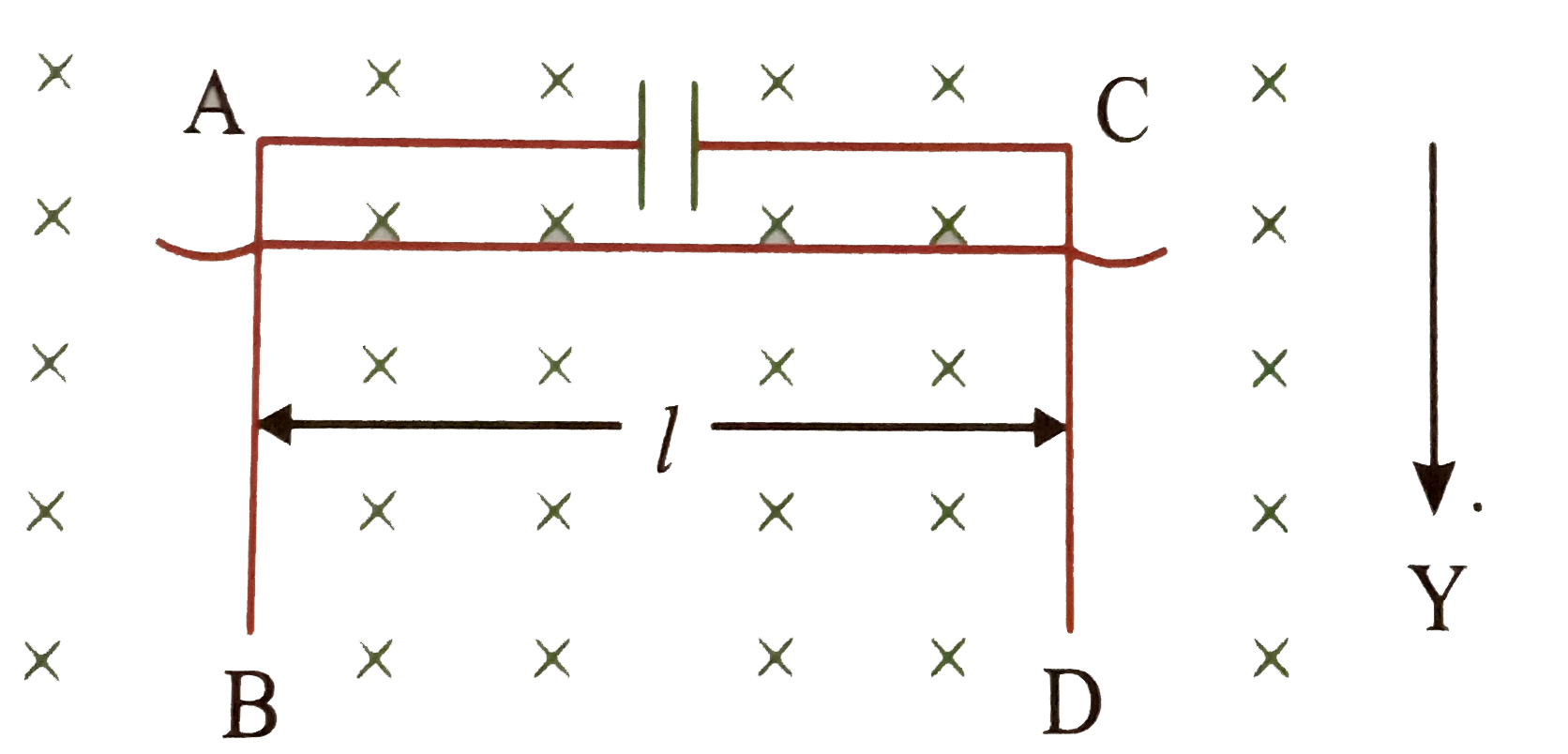
Based on above information answer the following questions:
Current in the circuit isAconstantBincreasing with timeCdecreasing with timeDFirst increase, then reaches a maximum value, and then starts decreasing to attain a constant value finallyA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.
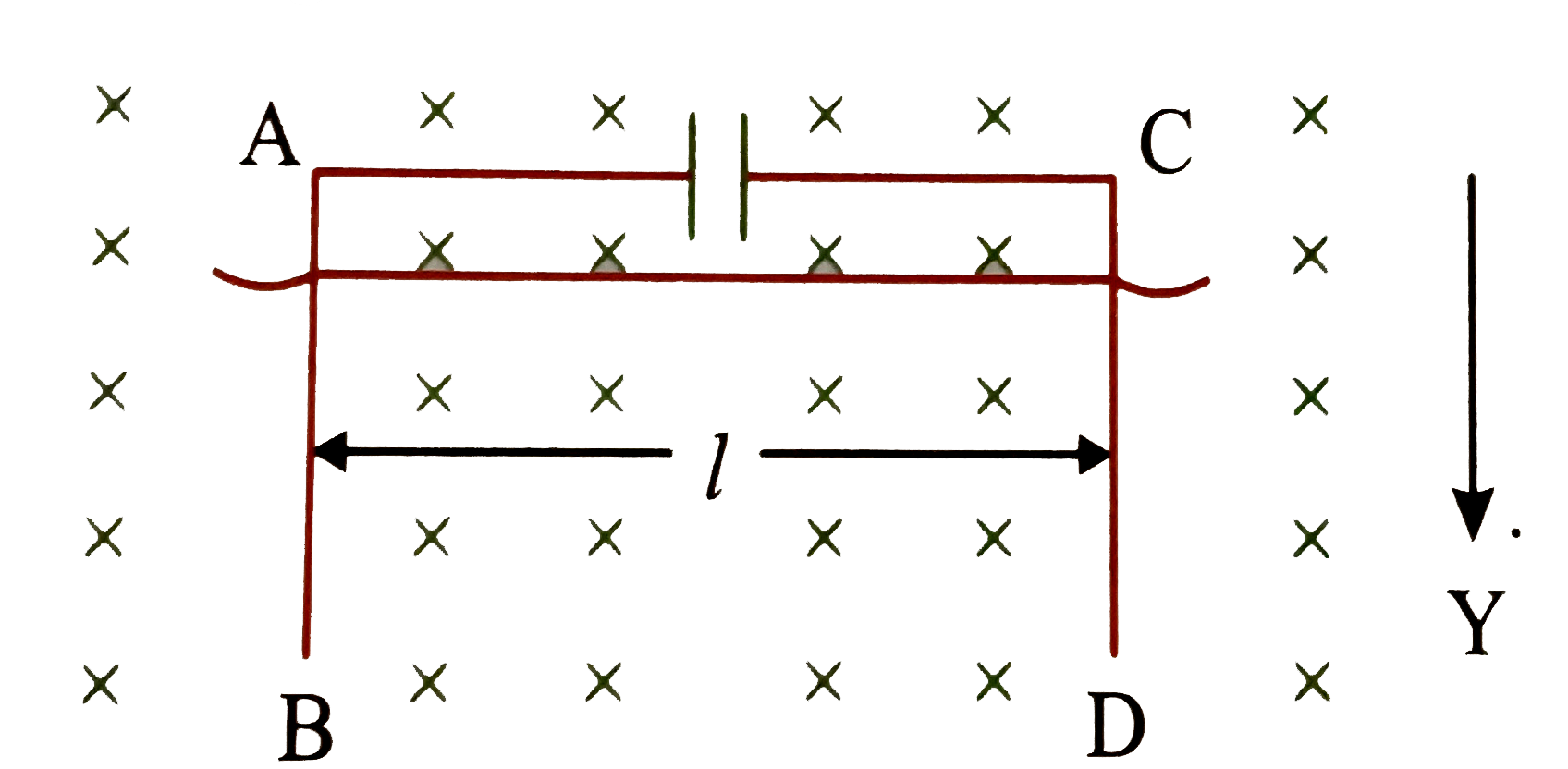
Based on above information answer the following questions:
Mark the correct statement about the motion of conductorAIt is falling down with constant acceleration gBIt is falling down with constant acceleration but not equal to gCIt is falling down with increasing accelerationDIt is falling down with decreasing accelerationA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.

Based on above information answer the following questions:
Charge on the capacitor as a function of distance travelled y is given byACB0l√2mgym+CB20l2BCB0l√m+CB20l22mgyCCB0lemgym+CB20l2DCB0l√2mgym+CB20l2×emgym+CB20l2
A conducting rod AB of mass m, has negligible resistance and of length 0.5 m slides on a pair of parallel metalic rails, which are connected by a resistance R=10Ω and capacitance C=1μF as shown in the figure. A magnetic field B=1T is applied normal and into the plane of the circuit. At tim t=0 a force F=0.4N is applied on the rod AB. What will be the terminal speed acquired by rod?
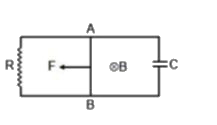
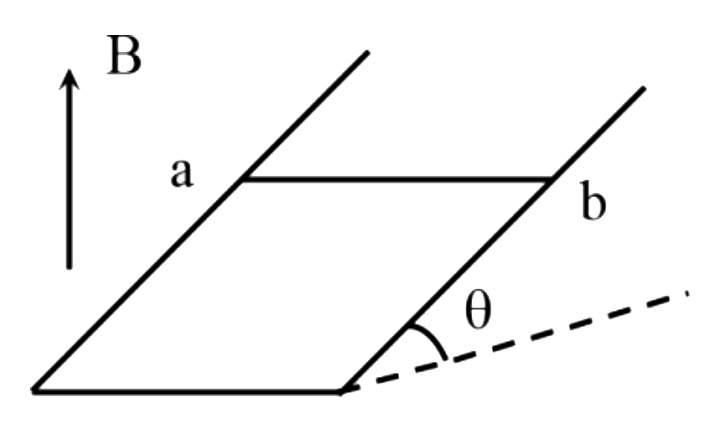
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View SolutionA horizontal wire is free to slide on the vertical rails of a conducting frame as shown in figure. The wire has a mass m and length l and the resistance of the circuit is R. If a uniform magnetic field B is directed perpendicular to the frame, the terminal speed of the wire as it falls under the force of gravity is

View SolutionA conducting wire is moving towards right in a magnetic field B. The direction of induced current in the wire is shown in the figure. The direction of magnetic field will be

View SolutionA wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.

View Solution
