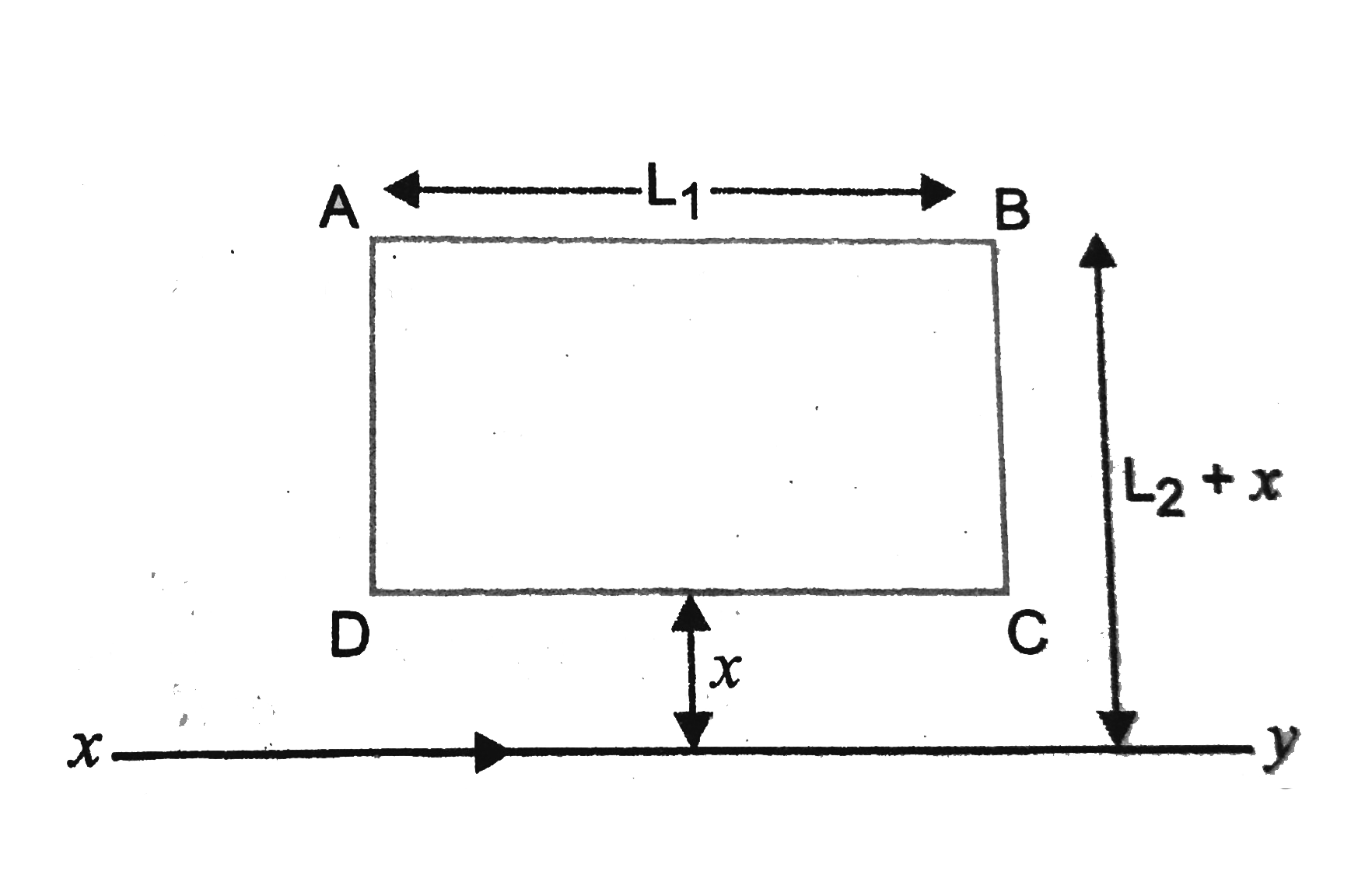
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I (t) =I0(1−t/T) for 0≤t≤T and I(0) = 0 for t>T, Fig. Find the total charge passing through a given point in the loop, in time T. resistance of the loop is R
The emf induced can be obtained by differentiating the expression on magnetic flux linked wrt t and then applying Ohm's law
I=ER=1Rdϕdt
We know that electric current I(t)=dQdtorDqdt=1dϕRdt
Integrating the variable separable form of differential equation for finding the charge Q that passed in time t, we have
Q(t1)−Q(t2)=1R[ϕ(t1)−ϕ(t2)]
ϕ(t1)=L1μ02π∫L2+xxdx1x1I(t1) [Refer to the Eq. (i) of answer no. 25]
=μ0L12πI(t1)InL2+xx
The magnitude of charge is given by , =μ0L12πInL2+xx[I0=0]
=μ0L12πI1In(L2+xx)
This is the required expression .
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Short answer type questions5videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question6videos
ELECTRIC CHARGES AND FIELD
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER5videos
ELECTROMAGNETIC WAVES
Similar Questions
a rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
 View Solution
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
 View Solution
View SolutionConsider an infinitely long wire carrying a current I (t),
With dIdt=λ = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig
 View Solution
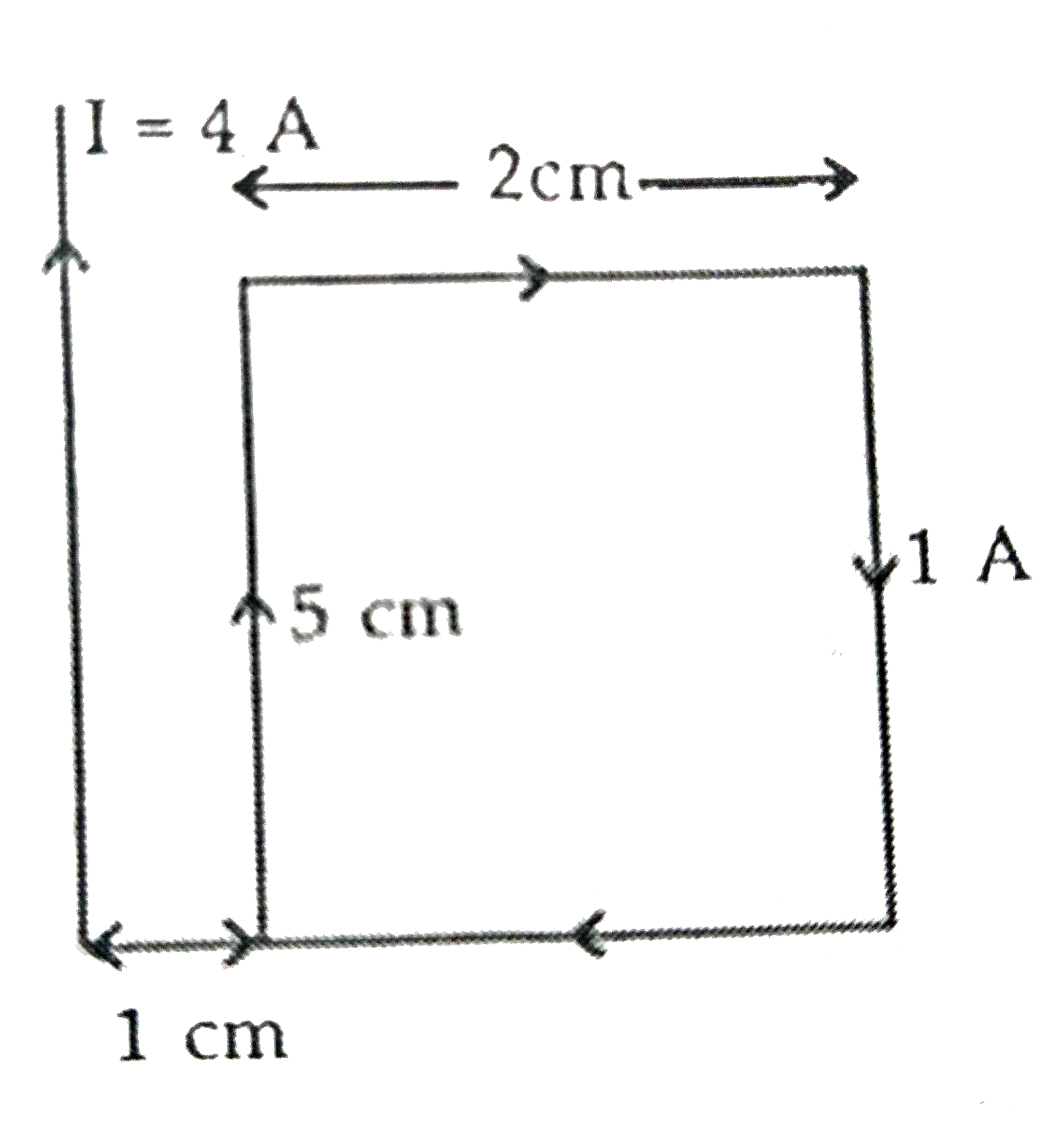
View SolutionA rectangular loop of wire of size 2cm×5cm carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the end
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
 View Solution
View SolutionThe circle passing through the points (1, t), (t, 1) and (t, t) for all values of t passes through the point
View SolutionA rectangular loop of wire of size 4cm×10cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
 View Solution
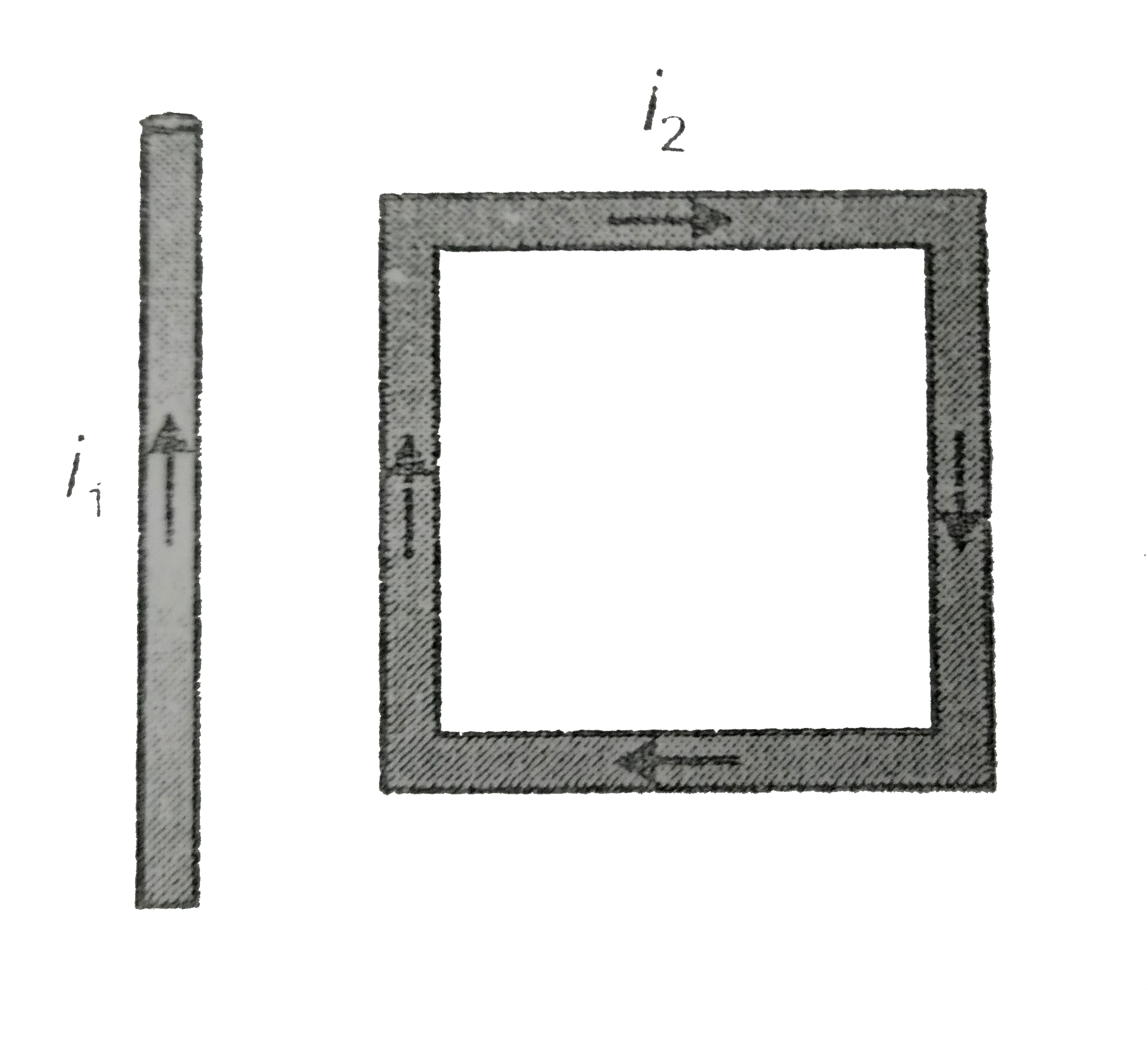
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
 View Solution
View SolutionCurrent in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.View SolutionThe current through a wire depends on time as, i=(10+4t) Here , i is ampere and t in seconds. Find the charge crossed through section in time interval between t=0 to t=10s.
View Solution
