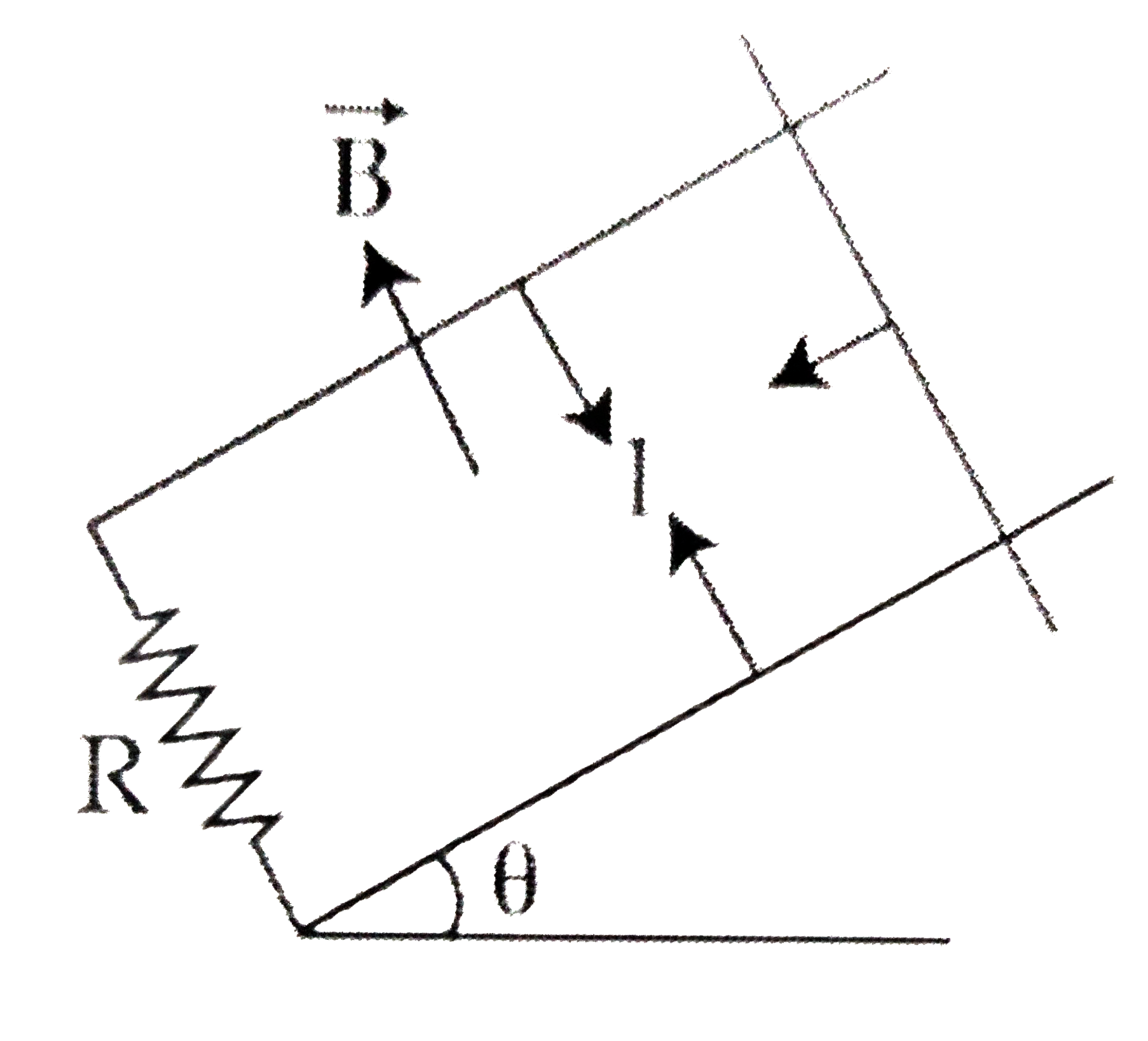
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horiaontal, Fig. The circuit is closed through a perfert conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.
Here, the component of magnetic field perpendicular the plane =Bcosθ Now, the conductor moves with speed v perpendicular to Bcosθ component of magnetic field. This causes motional emf across two ends of rod, which is given by =v(Bcosθ)d
This makes flow of induced current i=v(Bcosθ)dRwhere, R is the resistance of rod. Now, current carrying rod experience force which is given by F=iBd (horizontally in backward direction). Now, the component of magnetic force parallel to incline plane along upward direction =Fcosθ=v(Bcosθ)dRBdcosθ when, v=dxdt
Also, the component weight (mg) parallel to incline plane along donward direction =mgsinθ.
Now, by Newton's second law of motion
md2dt2=mgsinθ−BcosθdR(dxdt)×(Bd)cosθ
dvdt=gsinθ−B2d2mR(cosθ)2v
dvdt+B2d2mR(cosθ)2v=gsinθ
But this is the linear differential eqation. On solving we get
v=gsinθB2d2cos2θmR+Aexp(−B2d2mR(cos2θ)t)
A is a constant to be determine by intial conditions.
The required expression of velocity as a function of time is given by
=mgRsinθB2d2cos2θ(1−exp(−B2d2mR(cos2θ)t))
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Short answer type questions
5 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
Similar Questions
A conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t)ˆk
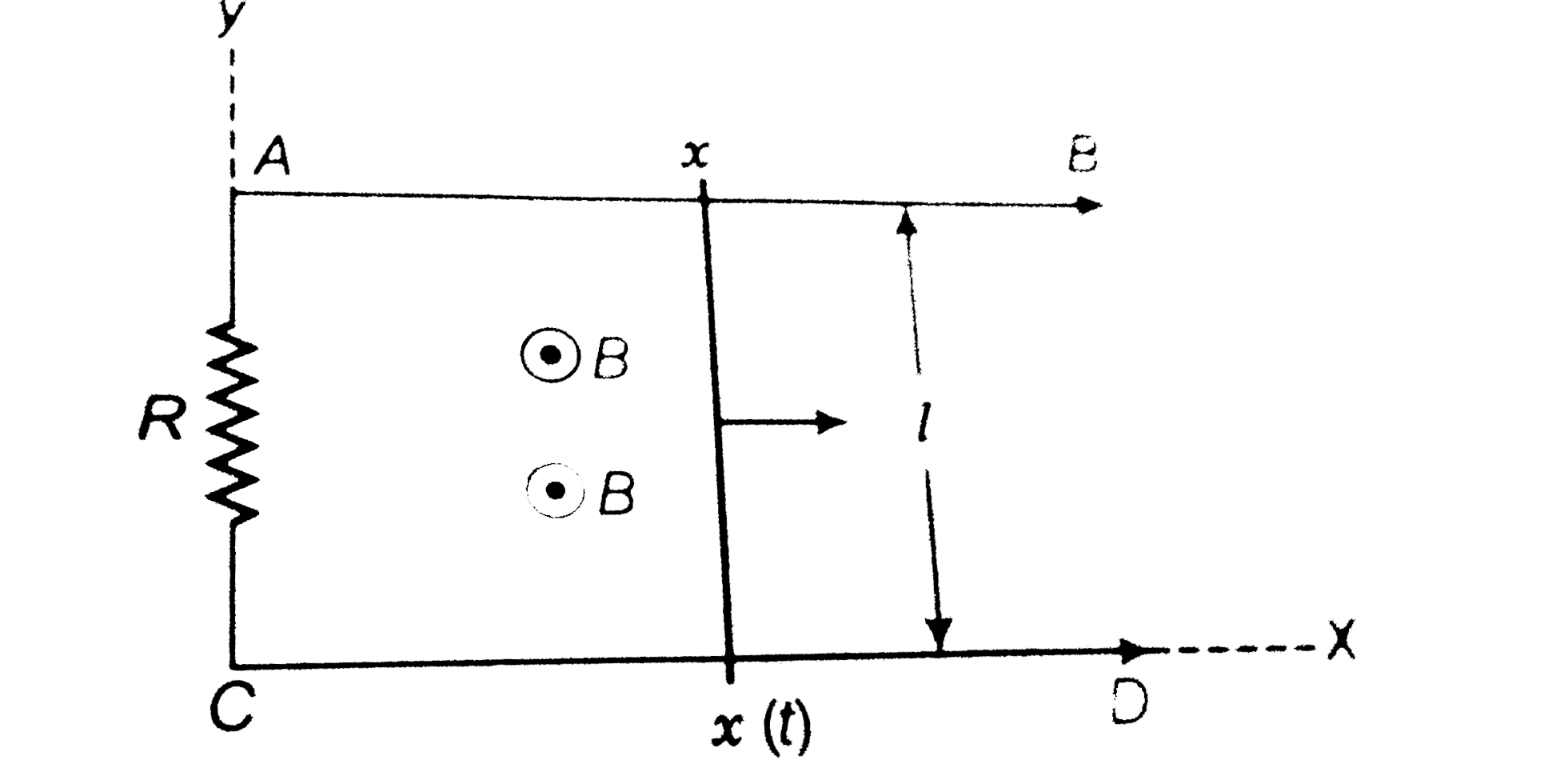
View SolutionA uniform rod AB of mass m and length l is placed over two smooth conducting rails P and Q. If the witch shown as closed at t=0, find the velocity of rod AB as a function of time.
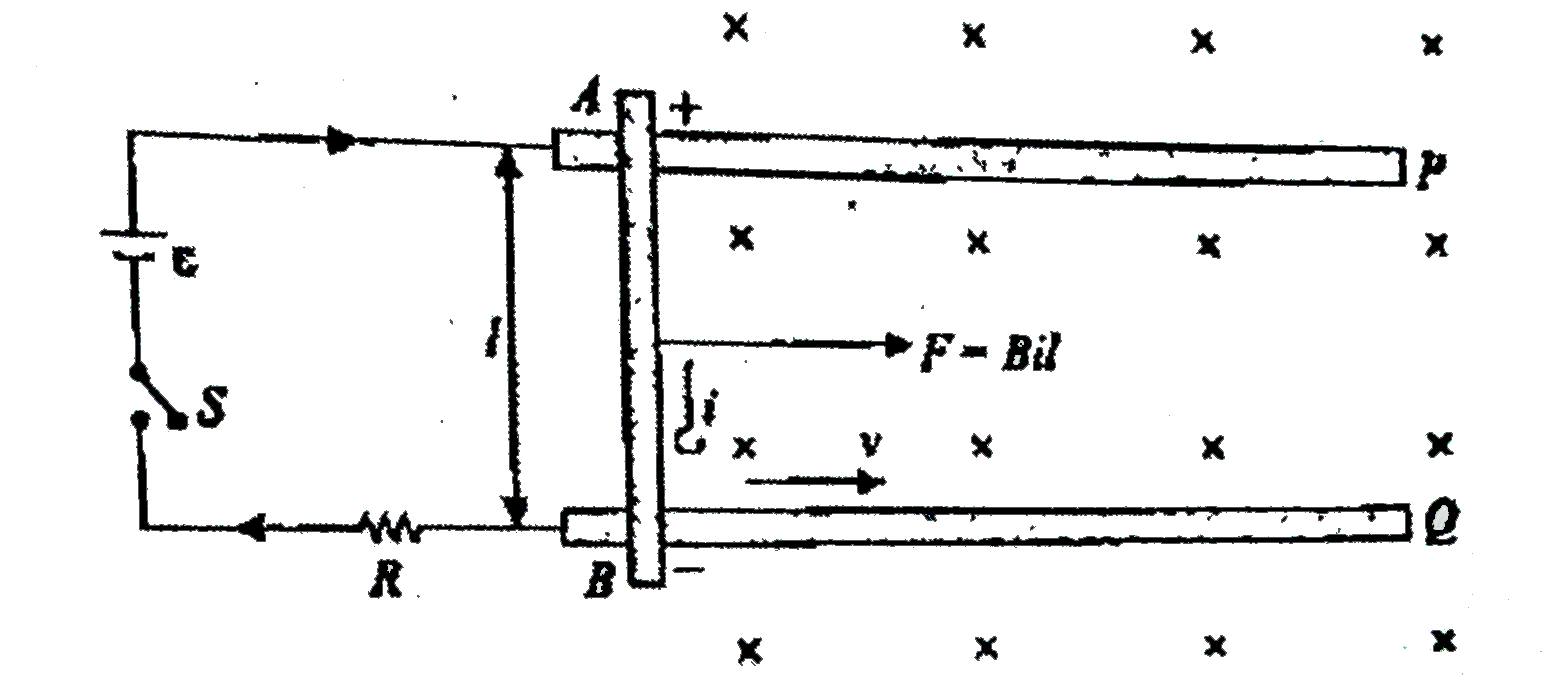
View Solution
Knowledge Check
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRtanθB2l2BmgRcotθB2l2CmgRsinθB2l2DmgRcosθB2l2A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
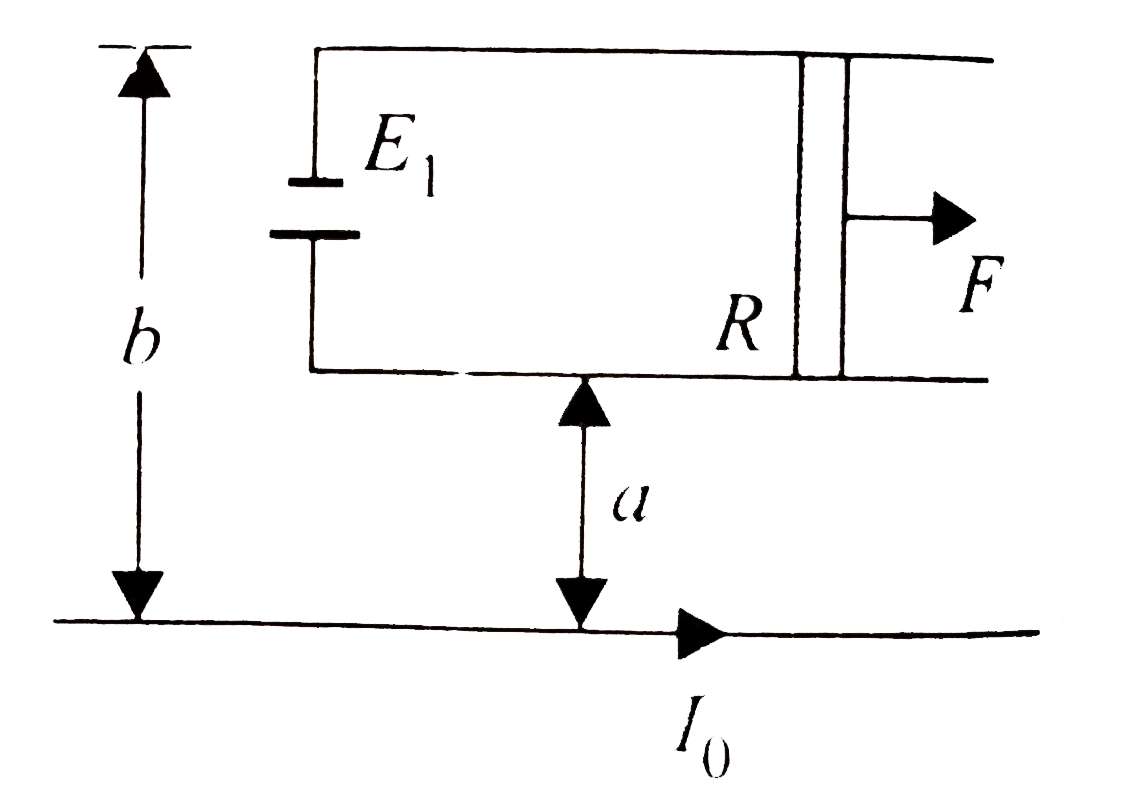
Find the value of current in the circuit if the rod slides with constant velocity v0A1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}B1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}C1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}DNone of these
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
View Solution
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
View SolutionA rod of mass m and resistance r is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance R) and it is projected with an initial velocity u.Find its velocity as a function of time.

View SolutionA rod of mass m and resistance r is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance R) and it is projected with an initial velocity u.Find its velocity as a function of time.

View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.

Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
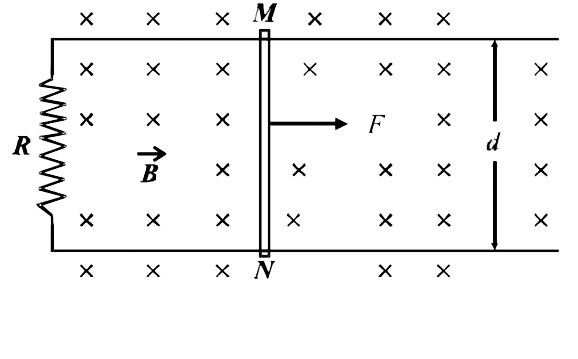
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
View Solution
