An infinite number of charges, each of coulomb, are placed along x-axis at x=1m,3m,9m and so on. Calculate the electric field at the point x = 0 due to these charges if all the charges are of the same sign.
To calculate the electric field at the point x=0 due to an infinite number of charges placed along the x-axis at positions x=1m,3m,9m,…, we can follow these steps:
Step 1: Identify the positions of the charges
The charges are placed at:
- x1=1m
- x2=3m
- x3=9m
- and so on.
These positions can be expressed as xn=2n−1 for n=1,2,3,….
Step 2: Calculate the distance from each charge to the point x=0
The distances from each charge to the point x=0 are:
- r1=1m
- r2=3m
- r3=9m
- and so on.
Step 3: Write the expression for the electric field due to a single charge
The electric field E due to a single charge Q at a distance r is given by:
E=14πϵ0Qr2
Since all charges are of the same sign, the direction of the electric field at x=0 will be away from the charges.
Step 4: Calculate the total electric field at x=0
The total electric field Etotal at x=0 due to all the charges can be expressed as:
Etotal=E1+E2+E3+…
Substituting the expression for E:
Etotal=Q4πϵ0(112+132+192+…)
Step 5: Identify the series
The series inside the parentheses is:
∞∑n=01(2n)2=∞∑n=014n
This is a geometric series with first term a=1 and common ratio r=14.
Step 6: Calculate the sum of the series
The sum of an infinite geometric series is given by:
S=a1−r
Substituting the values:
S=11−14=134=43
Step 7: Substitute back into the expression for Etotal
Now substituting back into the expression for Etotal:
Etotal=Q4πϵ0⋅43
Thus,
Etotal=Q3πϵ0
Final Answer
The electric field at the point x=0 due to these charges is:
E=Q3πϵ0
The charges are placed at:
- x1=1m
- x2=3m
- x3=9m
- and so on.
The distances from each charge to the point x=0 are:
- r1=1m
- r2=3m
- r3=9m
- and so on.
The electric field E due to a single charge Q at a distance r is given by:
E=14πϵ0Qr2
Since all charges are of the same sign, the direction of the electric field at x=0 will be away from the charges.
The total electric field Etotal at x=0 due to all the charges can be expressed as:
Etotal=E1+E2+E3+…
Substituting the expression for E:
Etotal=Q4πϵ0(112+132+192+…)
The series inside the parentheses is:
∞∑n=01(2n)2=∞∑n=014n
This is a geometric series with first term a=1 and common ratio r=14.
The sum of an infinite geometric series is given by:
S=a1−r
Substituting the values:
S=11−14=134=43
Now substituting back into the expression for Etotal:
Etotal=Q4πϵ0⋅43
Thus,
Etotal=Q3πϵ0
The electric field at the point x=0 due to these charges is:
E=Q3πϵ0
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET II8videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET III7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
An infinite number of charges each equal to q, are placed along the X-axis at x=1,x=2,x=4,x=8,…….. and so on.
(i) find the electric field at a point x=0 due to this set up of charges.
(ii) What will be the electric field if the above setup, the consecutive charges have opposite signs.View SolutionAn infinite number of charges, each equal to Q=10μC are placed along the x-axis at x=1,3,9…..m. Calculate the magnitude of electric field at x=0 if the consecutive charge have opposite signs.
View SolutionThree charges are placed along x- axis at x=−a,x=0 and x=a as shown . Calculate the potential energy of the system.
 View Solution
View SolutionCalculate the electric field at origin due to infinite number of charges as shown in figure below.
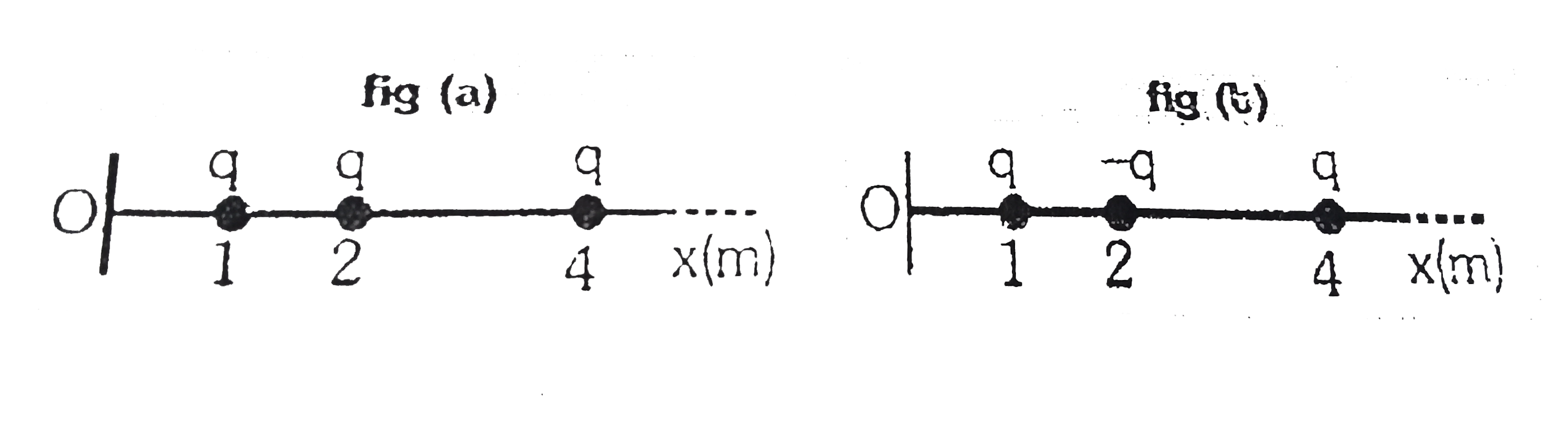 View Solution
View SolutionAn infinite number of charges, each of magnitude q, are placed along x-axis at x = 1m, 2m, 4m, 8m, 16m and so on but the consecutive charges are of opposite sign starting with +q at x = 1m. A point charge q0 , kept at the origin, experiences a force of magnitude :
View SolutionAn infinite number of electric charges each equal to 5 nano coulombs are placed along x-axis at x = 1 cm, x-2 cm, x -4 cm, x = 8 cm,.. and so on. In this setup, if the consecutive charges have opposite sign, then the electric field in newton/coulomb at x =0 is
View SolutionInfinite charges of magnitude q each are lying at x=1,2,4,8….meter on X-axis. The value of intensity of electric field at point x=0 due to these charges will be
View SolutionAn assembly of charges +q,−q,+q,−q….. are at positions x=1m,2m,4m,8m,…. And so on from origin. What is the potential at x=0, due to these charges ?
View SolutionAn infinite number of charges, each of charge 1μC are placed on the x-axis with co-ordinates x=1,2,4,8….∞ If a charge of 1C is kept at the origin, then what is the net force action on 1C charge
View SolutionThree charges are placed along x-axis at x = - a x = 0 and x = a as shown in the figure. The potential energy of the system is
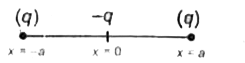 View Solution
View Solution

