Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
To solve the problem of tracing the rays of light and establishing the relationship between the distances of the object, image, and the radius of curvature of a spherical surface separating two media of refractive indices n1 and n2, we will follow these steps:
Step 1: Diagram Setup
1. Draw the Spherical Surface: Start by drawing a spherical surface with the center of curvature C and the pole P.
2. Label the Media: Indicate the denser medium (with refractive index n2) on one side of the spherical surface and the rarer medium (with refractive index n1) on the other side.
3. Place the Object: Position the point object O on the principal axis at a distance U from the pole P.
Step 2: Ray Tracing
1. Draw the Incident Ray: Draw a ray from the object O towards the spherical surface, hitting it at point Q.
2. Draw the Normal: At point Q, draw the normal line n from the center of curvature C to point Q.
3. Apply Snell's Law: According to Snell's law, when light travels from a rarer medium to a denser medium, it bends towards the normal. Thus, the ray will refract at point Q into the denser medium.
Step 3: Angles and Relationships
1. Define Angles: Let I be the angle of incidence, R be the angle of refraction, α be the angle between the incident ray and the principal axis, β be the angle between the refracted ray and the principal axis, and γ be the angle between the normal and the principal axis.
2. Apply Snell's Law: Write down Snell's law at point Q:
n1sinI=n2sinR
For small angles, sinI≈I and sinR≈R, leading to:
n1I=n2R
Step 4: Triangle Relationships
1. Use Triangle OQC: In triangle OQC:
I=α+γ
2. Use Triangle CQI: In triangle CQI:
γ=R+β⟹R=γ−β
Step 5: Substitute and Simplify
1. Substitute the expressions for I and R into Snell's law:
n1(α+γ)=n2(γ−β)
2. Express tan functions for angles α, β, and γ using small angle approximations:
- tanα=QMOM
- tanβ=QMIM
- tanγ=QMCM
Step 6: Establish the Relationship
1. Combine the equations to find a relationship between U, V, and R:
n1−U+n1R=n2R−n2V
2. Rearranging gives the lens formula:
n1−U+n2V=n2−n1R
Step 7: Derive the Lens Maker's Formula
1. For a lens with two surfaces, apply the above relationships to both surfaces and derive the final expression:
1F=(n2−n1n1)(1R1−1R2)
where F is the focal length of the lens.
1. Draw the Spherical Surface: Start by drawing a spherical surface with the center of curvature C and the pole P.
2. Label the Media: Indicate the denser medium (with refractive index n2) on one side of the spherical surface and the rarer medium (with refractive index n1) on the other side.
3. Place the Object: Position the point object O on the principal axis at a distance U from the pole P.
1. Draw the Incident Ray: Draw a ray from the object O towards the spherical surface, hitting it at point Q.
2. Draw the Normal: At point Q, draw the normal line n from the center of curvature C to point Q.
3. Apply Snell's Law: According to Snell's law, when light travels from a rarer medium to a denser medium, it bends towards the normal. Thus, the ray will refract at point Q into the denser medium.
1. Define Angles: Let I be the angle of incidence, R be the angle of refraction, α be the angle between the incident ray and the principal axis, β be the angle between the refracted ray and the principal axis, and γ be the angle between the normal and the principal axis.
2. Apply Snell's Law: Write down Snell's law at point Q:
n1sinI=n2sinR
For small angles, sinI≈I and sinR≈R, leading to:
n1I=n2R
1. Use Triangle OQC: In triangle OQC:
I=α+γ
2. Use Triangle CQI: In triangle CQI:
γ=R+β⟹R=γ−β
1. Substitute the expressions for I and R into Snell's law:
n1(α+γ)=n2(γ−β)
2. Express tan functions for angles α, β, and γ using small angle approximations:
- tanα=QMOM
- tanβ=QMIM
- tanγ=QMCM
1. Combine the equations to find a relationship between U, V, and R:
n1−U+n1R=n2R−n2V
2. Rearranging gives the lens formula:
n1−U+n2V=n2−n1R
1. For a lens with two surfaces, apply the above relationships to both surfaces and derive the final expression:
1F=(n2−n1n1)(1R1−1R2)
where F is the focal length of the lens.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET II
8 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET III
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B
7 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
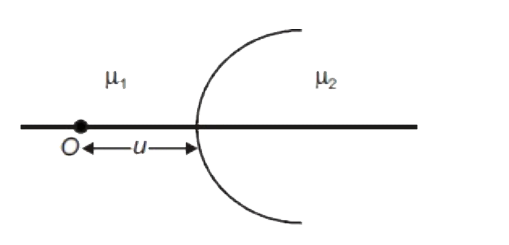
View SolutionA convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
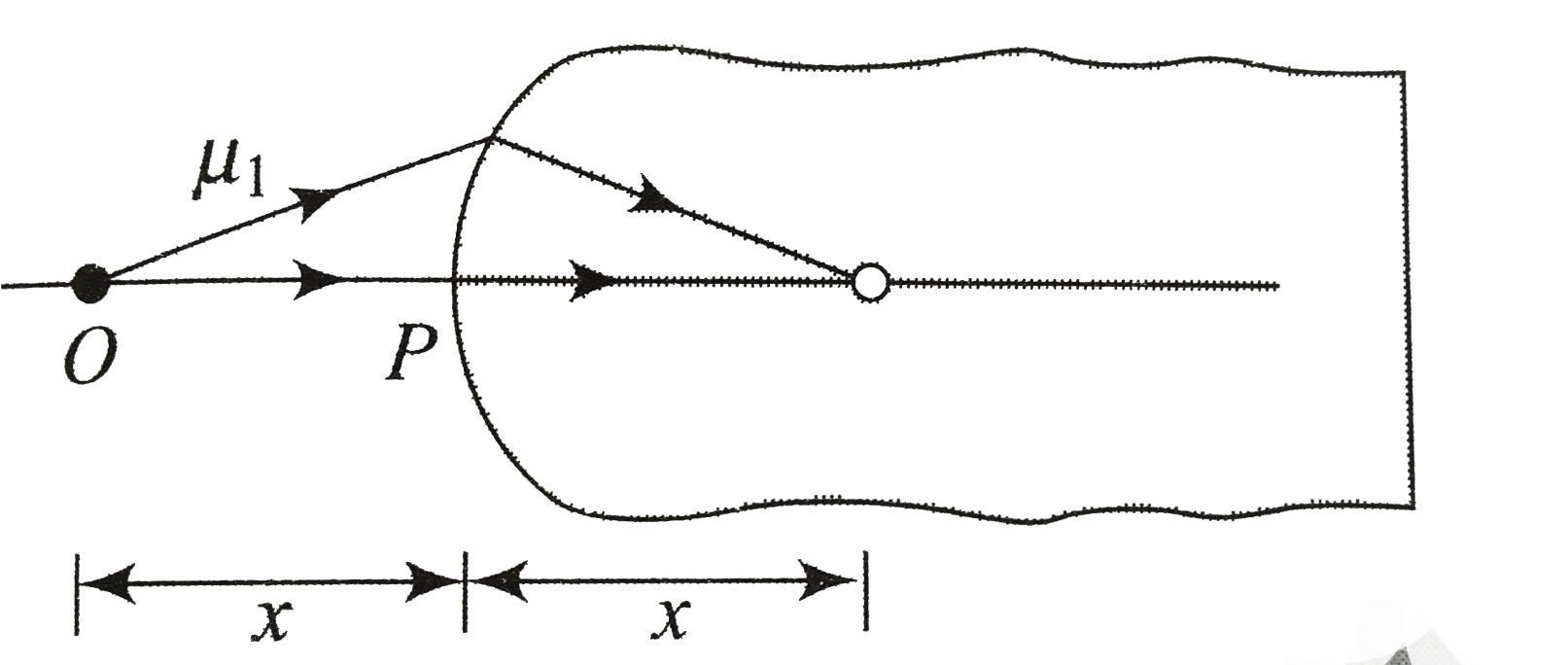
View SolutionObtain an expression for refraction at a single convex spherical surface separating the two media having refractive indices μ1(rarer medium) and μ2(denser medium) i.e., a relation between u,v,μ1,μ2 and R.
View SolutionIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is

View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View SolutionIn Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
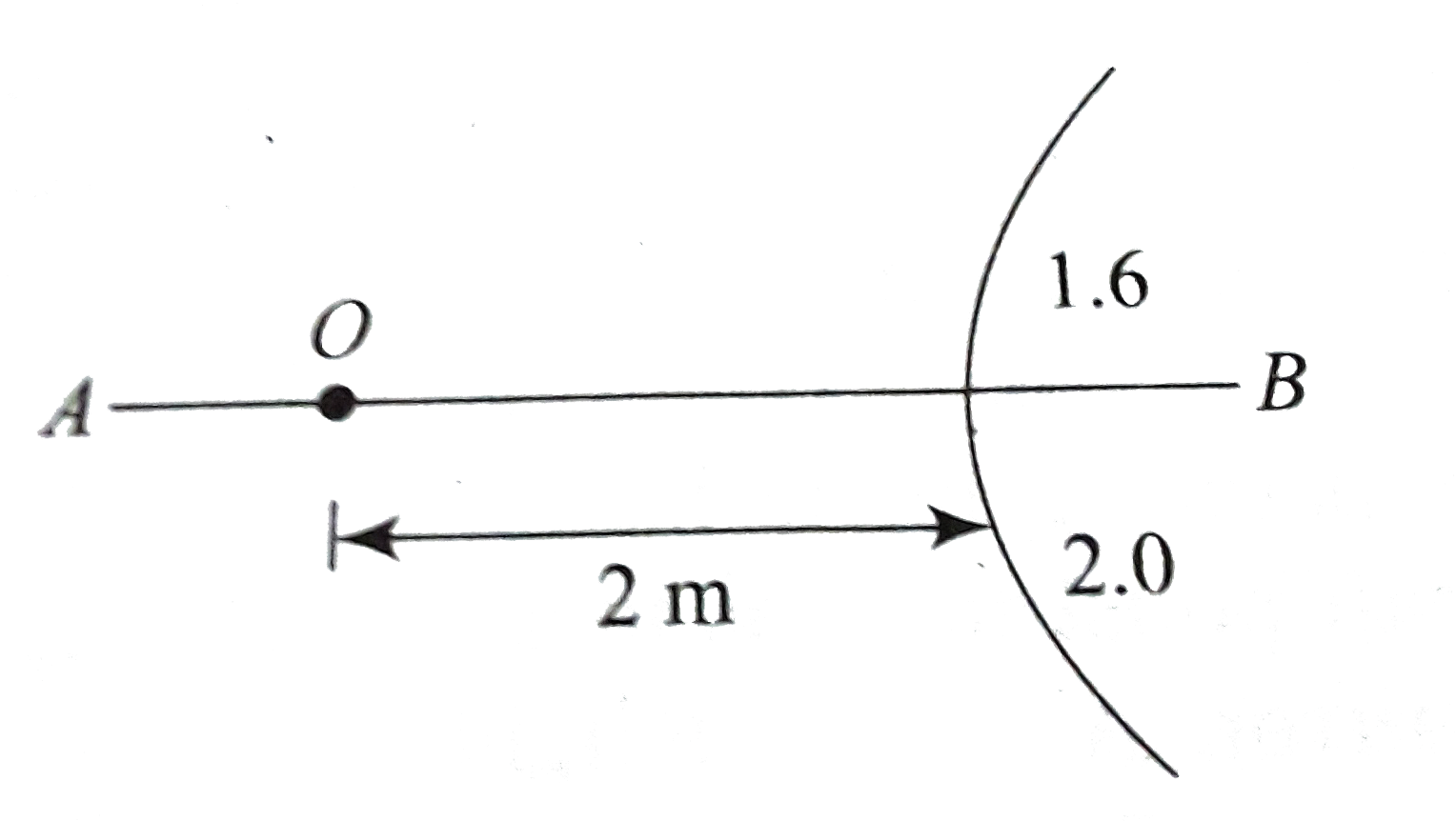
View SolutionIn a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
View SolutionA convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
View Solution
