An infinite number of charges, each of charge 1μC are placed on the x-axis with co-ordinates x=1,2,4,8….∞ If a charge of 1C is kept at the origin, then what is the net force action on 1C charge
9000 N
12000 N
24000 N
36000 N
The correct Answer is:B
To solve the problem, we need to calculate the net force acting on a charge of 1C placed at the origin due to an infinite number of charges of 1μC located at positions x=1,2,4,8,… on the x-axis.
1. Identify the Charges and Their Positions:
- The charge at the origin is Q=1C.
- The charges on the x-axis are q=1μC=1×10−6C located at x=1,2,4,8,….
2. Determine the Distance of Each Charge from the Origin:
- The distances of the charges from the origin are r1=1, r2=2, r3=4, r4=8, and so on.
3. Calculate the Force Due to Each Charge:
- The force F between two point charges is given by Coulomb's law:
F=k|Q⋅q|r2
- Here, k is Coulomb's constant, approximately 9×109N m2/C2.
4. Calculate the Net Force:
- The net force acting on the charge at the origin due to all the other charges can be expressed as:
Fnet=k⋅Q⋅q(1r21+1r22+1r23+…)
- Substituting the values:
Fnet=k⋅(1C)⋅(1×10−6C)(112+122+142+…)
5. Recognize the Series:
- The series 112+122+142+… can be rewritten as:
S=1+14+116+…
- This is a geometric series with the first term a=1 and common ratio r=14.
6. Sum the Infinite Series:
- The sum of an infinite geometric series is given by:
S=a1−r=11−14=134=43
7. Substitute Back into the Force Equation:
- Now substituting S back into the force equation:
Fnet=k⋅(1)⋅(1×10−6)⋅(43)
- Therefore:
Fnet=9×109⋅(1×10−6)⋅(43)
8. Calculate the Final Result:
- Simplifying gives:
Fnet=9×103⋅43=12,000N
Final Answer:
The net force acting on the 1C charge at the origin is 12,000N.
- The charge at the origin is Q=1C.
- The charges on the x-axis are q=1μC=1×10−6C located at x=1,2,4,8,….
- The distances of the charges from the origin are r1=1, r2=2, r3=4, r4=8, and so on.
- The force F between two point charges is given by Coulomb's law:
F=k|Q⋅q|r2
- Here, k is Coulomb's constant, approximately 9×109N m2/C2.
- The net force acting on the charge at the origin due to all the other charges can be expressed as:
Fnet=k⋅Q⋅q(1r21+1r22+1r23+…)
- Substituting the values:
Fnet=k⋅(1C)⋅(1×10−6C)(112+122+142+…)
- The series 112+122+142+… can be rewritten as:
S=1+14+116+…
- This is a geometric series with the first term a=1 and common ratio r=14.
- The sum of an infinite geometric series is given by:
S=a1−r=11−14=134=43
- Now substituting S back into the force equation:
Fnet=k⋅(1)⋅(1×10−6)⋅(43)
- Therefore:
Fnet=9×109⋅(1×10−6)⋅(43)
- Simplifying gives:
Fnet=9×103⋅43=12,000N
The net force acting on the 1C charge at the origin is 12,000N.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
An infinite number of charges each q are placed in the x-axis at distances of 1, 2, 4, 8, ………meter from the origin. If the charges are alternately positive and negative find the intensity of electric field at origin.
View SolutionAn infinite number of charges, each equal to Q=10μC are placed along the x-axis at x=1,3,9…..m. Calculate the magnitude of electric field at x=0 if the consecutive charge have opposite signs.
View Solution
Knowledge Check
The number of electrons present in -1 C of charge is
A6.25×1018B1.6×1019C6×1019D1.6×1018
An infinite number of charges, each of magnitude q, are placed along x-axis at x = 1m, 2m, 4m, 8m, 16m and so on but the consecutive charges are of opposite sign starting with +q at x = 1m. A point charge q0 , kept at the origin, experiences a force of magnitude :
View SolutionTwo point charge +2C and +6C repel each other with a force of 12N . If a charge of −4C is given to each other of these charges , the force will now be
View SolutionAn infinite number of charges, each of coulomb, are placed along x-axis at x=1m,3m,9m and so on. Calculate the electric field at the point x = 0 due to these charges if all the charges are of the same sign.
View SolutionAn infinite number of electric charges each equal to 5 nano coulombs are placed along x-axis at x = 1 cm, x-2 cm, x -4 cm, x = 8 cm,.. and so on. In this setup, if the consecutive charges have opposite sign, then the electric field in newton/coulomb at x =0 is
View SolutionTwo point charges +2C and +6C repel each other with a force of 12N. If a charge q is given the each of the these charges then they attract with 4N. Then value q is
View SolutionFor an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
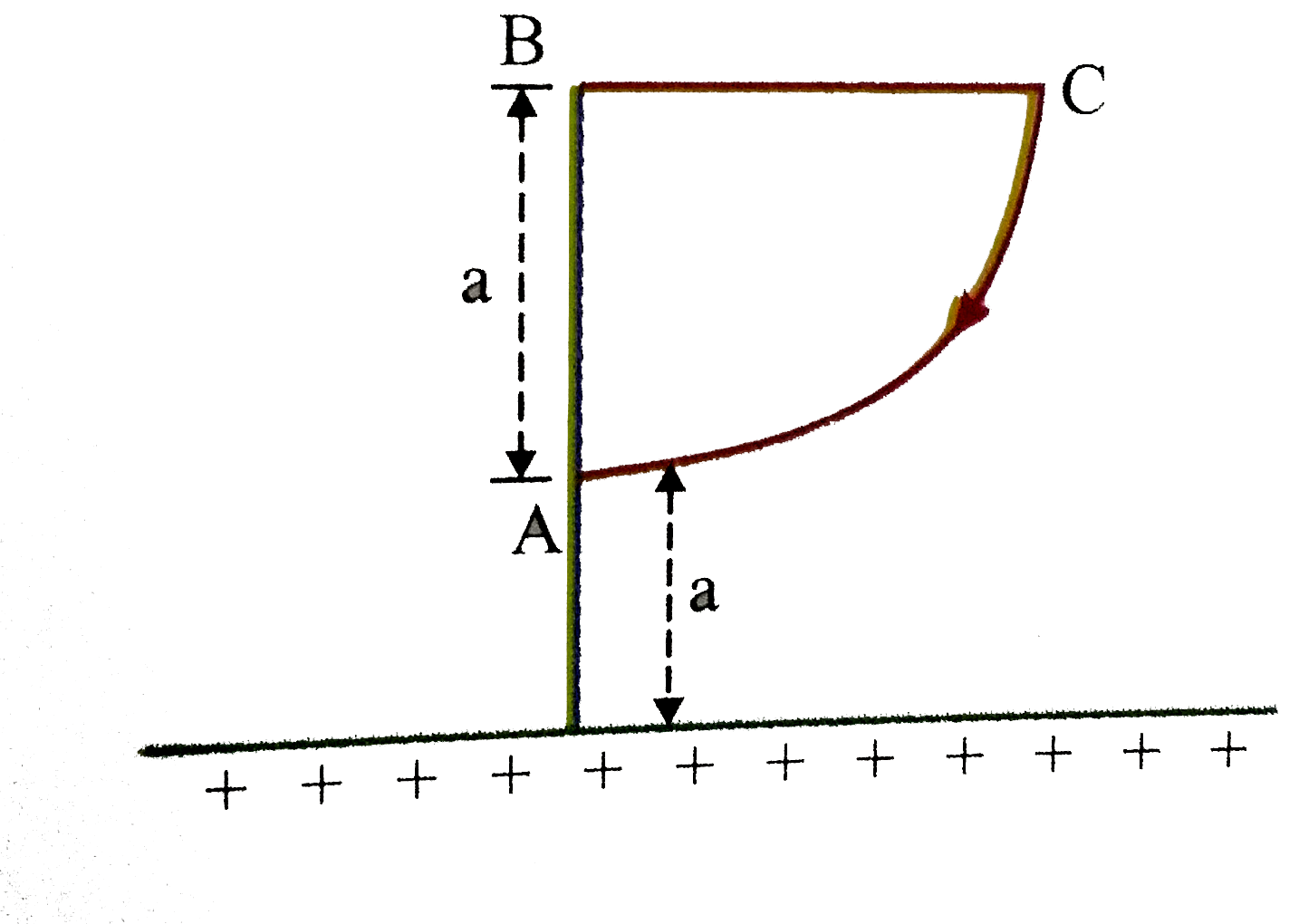
View SolutionTwo charges 9μCand1μC are placed at a distance of 30cm. The position of third charge from 9μC between them so that it does not experience any force.
View Solution
