A cell of emf E and internal resistance r is connected to two external resistance R1 and R2 and a perfect ammeter. The current in the circuit is measured in four different situations :
(i) without any external resistance in the circuit
(ii) with resistance R1 only
(iii) with R1 and R2 in series combination
(iv) with R1 and R2 in parallel combination
The currents measured in the four cases are 0.42A, 1.05 A, 1.4 A and 4.2 A, but not necessarily in that order. Identify the currents corresponding to the four cases mentioned above.
To solve the problem, we need to analyze the four situations in which the current is measured and identify which current corresponds to each situation.
1. Situation (i): Without any external resistance
- In this case, the only resistance in the circuit is the internal resistance r of the cell. The current will be maximum because there are no external resistances to limit it.
- The maximum current can be calculated using Ohm's law:
I=Er
- Since this is the maximum current, it corresponds to the highest measured current, which is 4.2 A.
2. Situation (ii): With resistance R1 only
- Here, the circuit consists of the cell with internal resistance r and the external resistance R1. The total resistance in the circuit is R1+r.
- The current can be calculated as:
I=ER1+r
- This current will be less than the maximum current (4.2 A) but more than the current in the series combination of R1 and R2. The next highest current is 1.05 A.
3. Situation (iii): With R1 and R2 in series
- In this case, the total resistance is R1+R2+r. The current can be calculated as:
I=ER1+R2+r
- Since the total resistance is greater than in the previous case, the current will be lower. This current corresponds to the lowest measured current, which is 0.42 A.
4. Situation (iv): With R1 and R2 in parallel
- For resistors in parallel, the equivalent resistance Req is given by:
1Req=1R1+1R2
- The total resistance in the circuit is Req+r. The current can be calculated as:
I=EReq+r
- Since the equivalent resistance is less than either R1 or R2, the current will be higher than in the series case. The remaining current is 1.4 A.
Summary of Currents:
- Situation (i): 4.2 A (without any external resistance)
- Situation (ii): 1.05 A (with R1 only)
- Situation (iii): 0.42 A (with R1 and R2 in series)
- Situation (iv): 1.4 A (with R1 and R2 in parallel)
- In this case, the only resistance in the circuit is the internal resistance r of the cell. The current will be maximum because there are no external resistances to limit it.
- The maximum current can be calculated using Ohm's law:
I=Er
- Since this is the maximum current, it corresponds to the highest measured current, which is 4.2 A.
- Here, the circuit consists of the cell with internal resistance r and the external resistance R1. The total resistance in the circuit is R1+r.
- The current can be calculated as:
I=ER1+r
- This current will be less than the maximum current (4.2 A) but more than the current in the series combination of R1 and R2. The next highest current is 1.05 A.
- In this case, the total resistance is R1+R2+r. The current can be calculated as:
I=ER1+R2+r
- Since the total resistance is greater than in the previous case, the current will be lower. This current corresponds to the lowest measured current, which is 0.42 A.
- For resistors in parallel, the equivalent resistance Req is given by:
1Req=1R1+1R2
- The total resistance in the circuit is Req+r. The current can be calculated as:
I=EReq+r
- Since the equivalent resistance is less than either R1 or R2, the current will be higher than in the series case. The remaining current is 1.4 A.
- Situation (i): 4.2 A (without any external resistance)
- Situation (ii): 1.05 A (with R1 only)
- Situation (iii): 0.42 A (with R1 and R2 in series)
- Situation (iv): 1.4 A (with R1 and R2 in parallel)
Similar Questions
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, verses 'R.
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solution
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A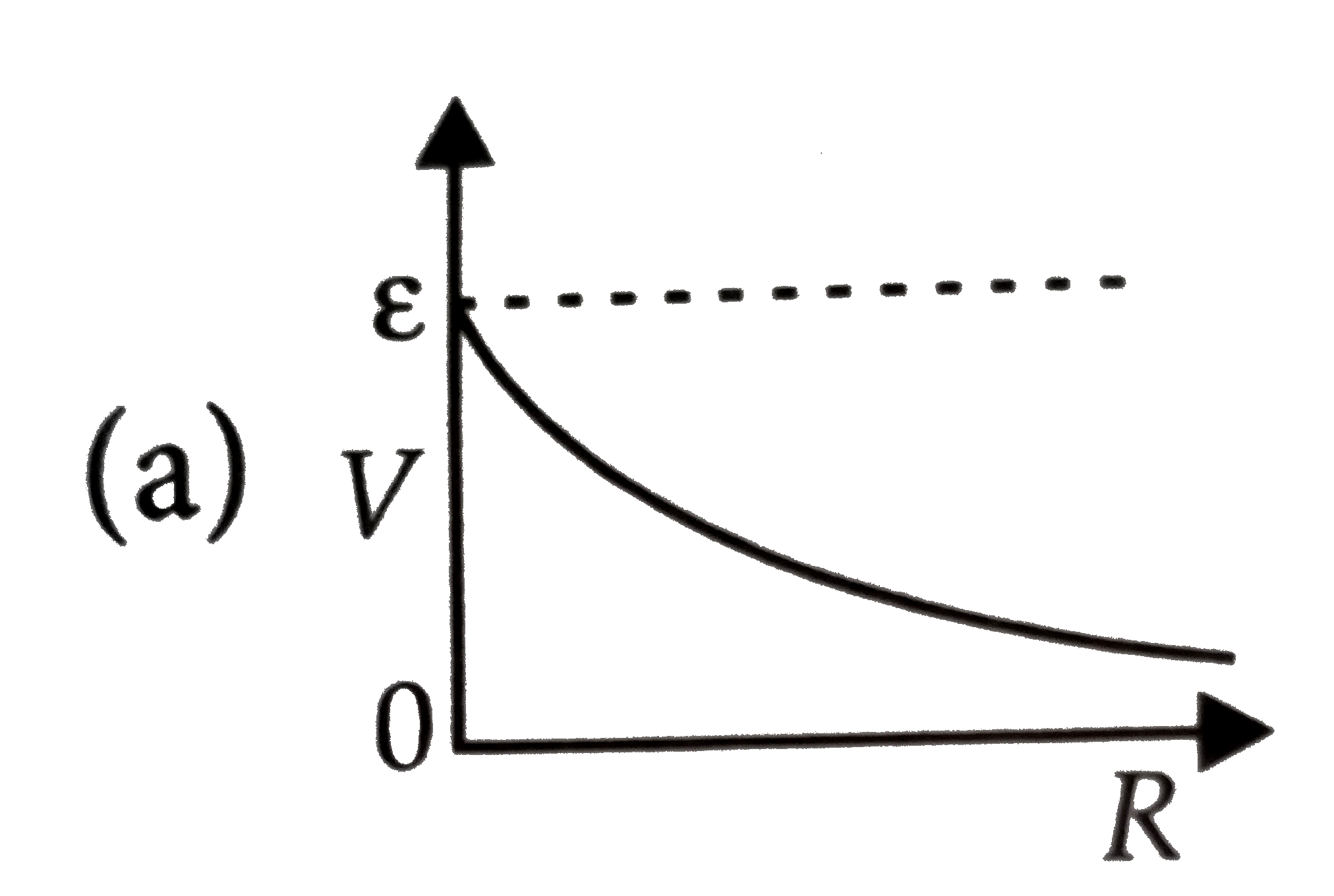 B
B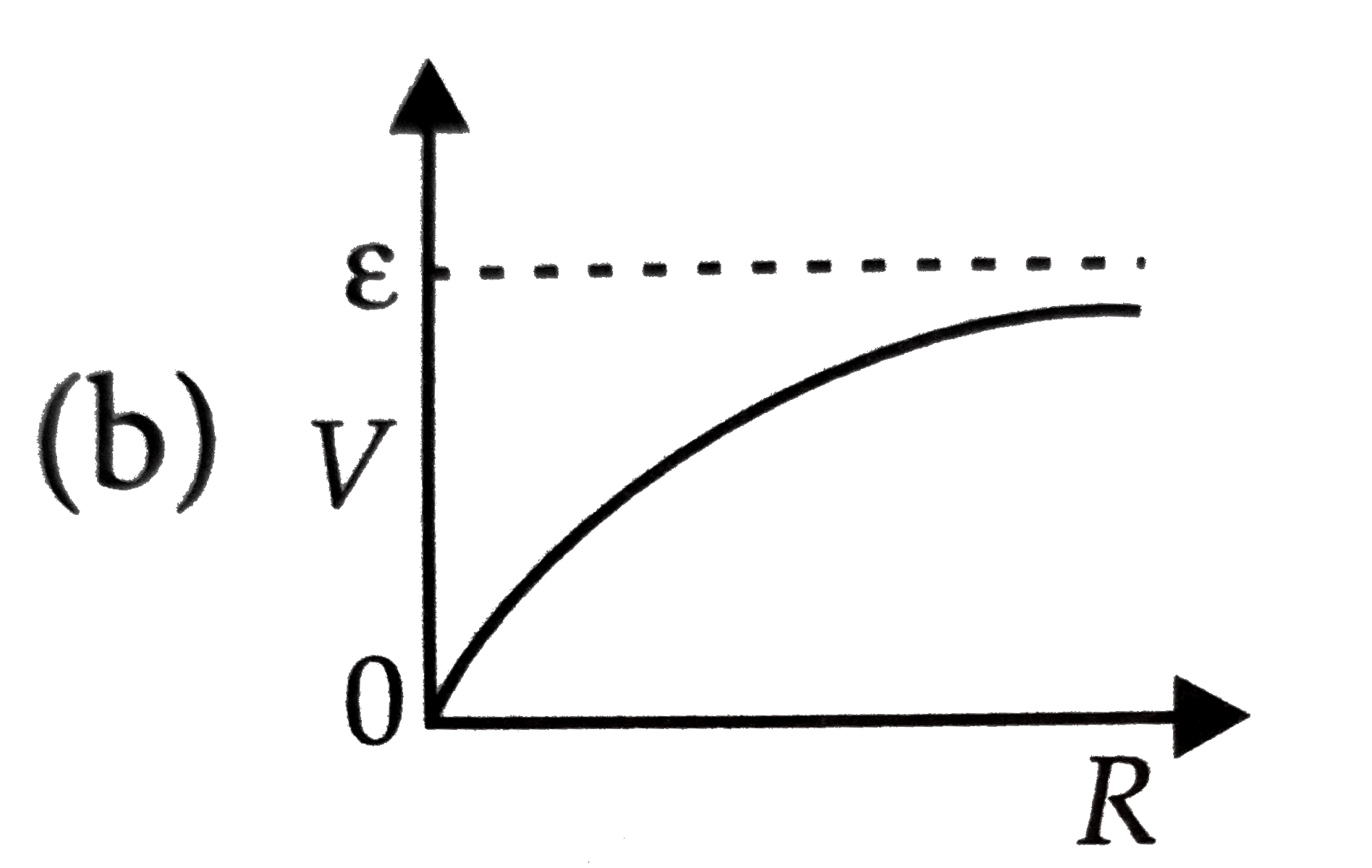 C
C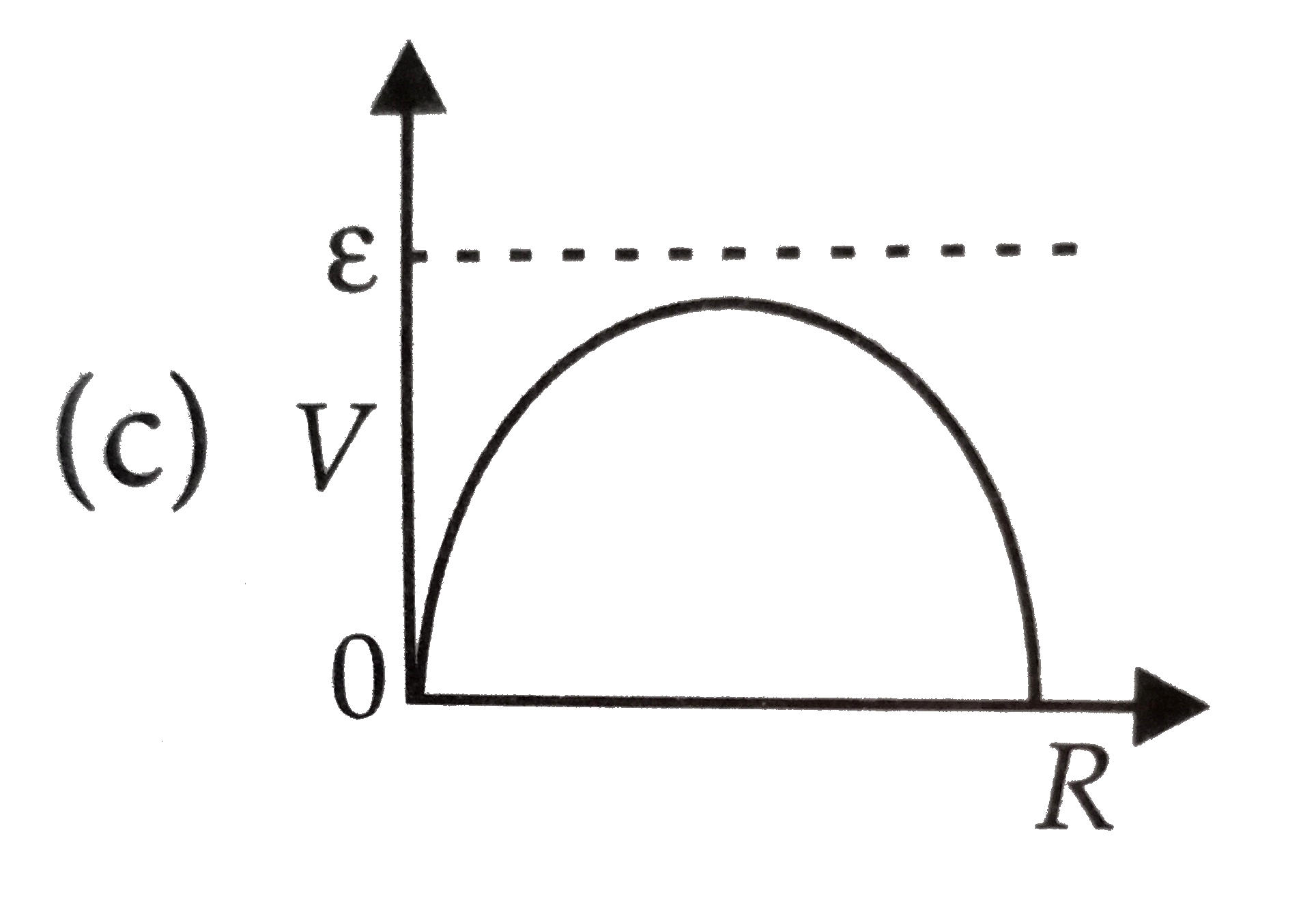 D
D
A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of emf E and internal resistance r supplies currents for the same time t through external resistances R1=100ΩandR2=40Ω separately. If the heat developed in both cases is the same, then the internal resistance of the cell is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell to emf. E and internal resistance r supplies currents for the same time t through external resistanceR1andR2 respectively. If the heat produced in both cases is the same, then the internal resistance is given by :
View Solution2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View Solution