Two cells having an internal resistance of and are connected in parallel (same polarity) the voltage across the battery is 1.5 V. If the emf of one cell is 1.2 V, then the emf of second cell is
The correct Answer is:2.1
To solve the problem, we need to find the EMF of the second cell (E2) when two cells with internal resistances of 0.2 Ω and 0.4 Ω are connected in parallel, and the voltage across the battery is 1.5 V. One cell has an EMF of 1.2 V.
1. Understanding the Circuit:
- We have two cells connected in parallel with the same polarity.
- The voltage across the combination is given as 1.5 V.
- The EMF of the first cell (E1) is 1.2 V, and its internal resistance (R1) is 0.2 Ω.
- The internal resistance of the second cell (R2) is 0.4 Ω, and we need to find its EMF (E2).
2. Applying Kirchhoff's Voltage Law:
- For the first cell (E1), the voltage across it can be expressed as:
V=E1−I⋅R1
- For the second cell (E2), the voltage across it can be expressed as:
V=E2+I⋅R2
- Since both cells are in parallel, the voltage across both cells is the same (1.5 V).
3. Setting Up the Equations:
- For the first cell:
1.5=1.2−I⋅0.2(1)
- For the second cell:
1.5=E2+I⋅0.4(2)
4. Solving Equation (1) for Current (I):
- Rearranging equation (1):
I⋅0.2=1.2−1.5
I⋅0.2=−0.3
I=−0.30.2=−1.5A
5. Substituting I into Equation (2):
- Substitute I into equation (2):
1.5=E2+(−1.5)⋅0.4
1.5=E2−0.6
E2=1.5+0.6=2.1V
Final Answer:
The EMF of the second cell (E2) is 2.1 V.
---
- We have two cells connected in parallel with the same polarity.
- The voltage across the combination is given as 1.5 V.
- The EMF of the first cell (E1) is 1.2 V, and its internal resistance (R1) is 0.2 Ω.
- The internal resistance of the second cell (R2) is 0.4 Ω, and we need to find its EMF (E2).
- For the first cell (E1), the voltage across it can be expressed as:
V=E1−I⋅R1
- For the second cell (E2), the voltage across it can be expressed as:
V=E2+I⋅R2
- Since both cells are in parallel, the voltage across both cells is the same (1.5 V).
- For the first cell:
1.5=1.2−I⋅0.2(1)
- For the second cell:
1.5=E2+I⋅0.4(2)
- Rearranging equation (1):
I⋅0.2=1.2−1.5
I⋅0.2=−0.3
I=−0.30.2=−1.5A
- Substitute I into equation (2):
1.5=E2+(−1.5)⋅0.4
1.5=E2−0.6
E2=1.5+0.6=2.1V
The EMF of the second cell (E2) is 2.1 V.
Similar Questions
A cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
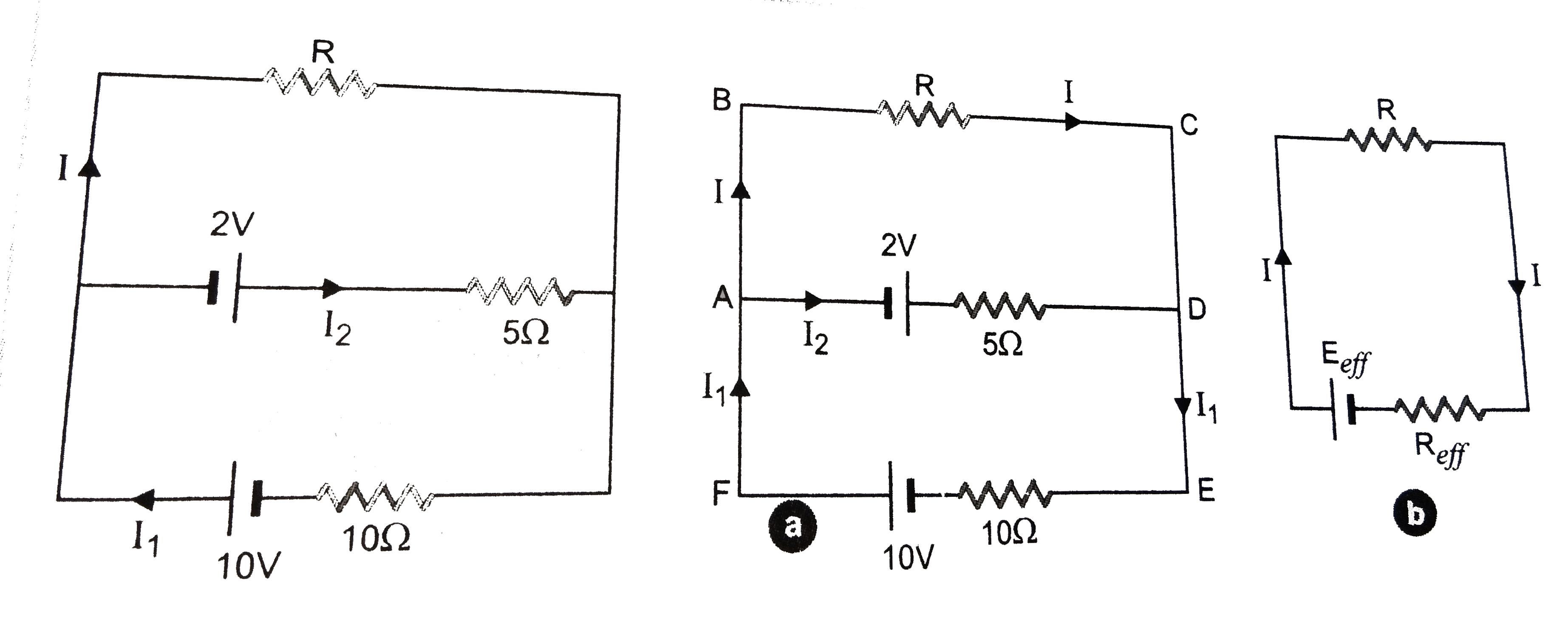
View SolutionTwo cells of voltage 10Vand 2V and internal resistance 10Ω and 5Ω respectively , are connected in parallel with the pesition and of 10V battery connected to negative pole of 2V battery Find the effected voltage and effected resistance of the combination
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThe series combination of two batteries, both of the same emf 20 V, but different internal resistance of 10 Ω and 2 Ω , is connected to the parallel combination of two resistors 10 ohm and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R(∈Ω) is _________.
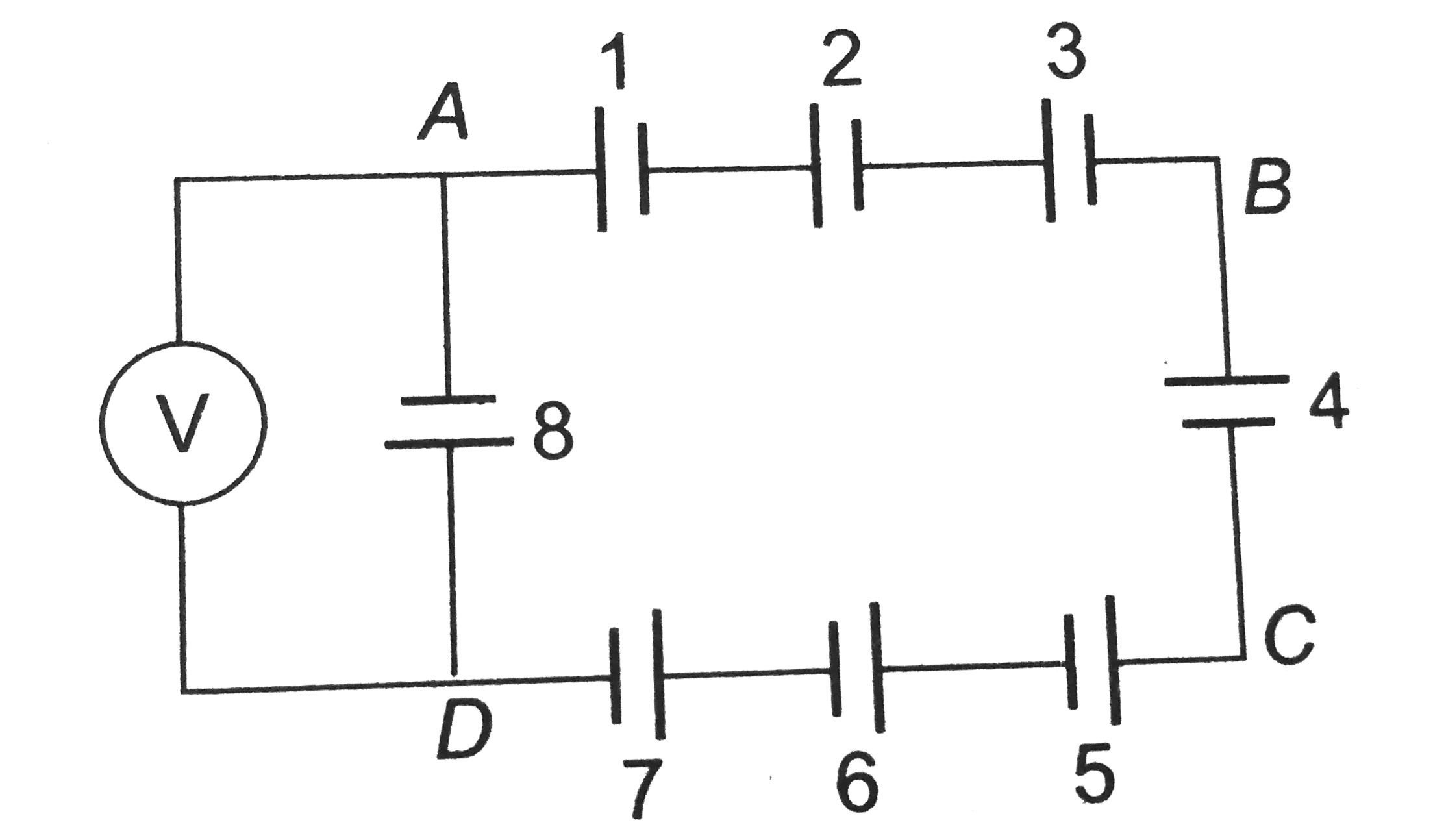
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View Solution
