A nucleus of mass number 240 and having binding energy/nucleon 7.6 MeV splits into two fragments Y, Z of mass numbers 110 and 130 respectively. If the binding energy/nucleon of Y, Z is equal to 8.5 MeV each, calculate the energy released in the nuclear reaction
To solve the problem step by step, we will calculate the binding energies of the original nucleus and the fragments, and then find the energy released in the nuclear reaction.
Step 1: Calculate the Binding Energy of the Original Nucleus (X)
The mass number of the original nucleus (X) is 240, and the binding energy per nucleon is 7.6 MeV.
Total Binding Energy of X=Mass Number×Binding Energy per Nucleon
Total Binding Energy of X=240×7.6 MeV=1824 MeV
Step 2: Calculate the Binding Energy of Fragment Y
The mass number of fragment Y is 110, and the binding energy per nucleon is 8.5 MeV.
Total Binding Energy of Y=Mass Number of Y×Binding Energy per Nucleon
Total Binding Energy of Y=110×8.5 MeV=935 MeV
Step 3: Calculate the Binding Energy of Fragment Z
The mass number of fragment Z is 130, and the binding energy per nucleon is also 8.5 MeV.
Total Binding Energy of Z=Mass Number of Z×Binding Energy per Nucleon
Total Binding Energy of Z=130×8.5 MeV=1105 MeV
Step 4: Calculate the Total Binding Energy of Fragments Y and Z
Total Binding Energy of Y and Z=Total Binding Energy of Y+Total Binding Energy of Z
Total Binding Energy of Y and Z=935 MeV+1105 MeV=2040 MeV
Step 5: Calculate the Energy Released in the Reaction
The energy released in the nuclear reaction (Q) can be calculated using the formula:
Q=Total Binding Energy of Y and Z−Total Binding Energy of X
Q=2040 MeV−1824 MeV=216 MeV
Final Answer
The energy released in the nuclear reaction is 216 MeV.
---
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]11videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-B52videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A heavy nucleus X of mass number 240 and binding energy per nucleon 7.6MeV is split into two fragments Y and Z of mass numbers 110 and 130. The binding energy of nucleons in Y and Z is 8.5MeV per nucleon. Calculate the energy Q released per fission in MeV.
View SolutionAs the mass number A increases, the binding energy per nucleon in a nucleus.
View Solution
Knowledge Check
- Question 1 - Select One
If the binding energy per nucleon of deuterium is 1.115 MeV, its mass defect in atomic mass unit is
A0.0048B0.0024C0.0012D0.0006 - Question 2 - Select One
The binding energy per nucleon of deuterium and helium nuclei are 1.1 MeV and 7.0 MeV respectively. When two deuterium nuclei fuse to form a helium nucleus the energy released in the fusion is
A23.6 MeVB2.2 MeVC28.0 MeVD30.2 MeV
A heavy nuleus having mass number 200 gets disintegrated into two small fragmnets of mass numbers 80 and 120. If binding energy per nulceon for parent atom is 6.5MeV and for daughter nuceli is 7MeV and 8MeV, respectivley , then the energy released in the decay will be.
View SolutionA heavy nuleus having mass number 200 gets disintegrated into two small fragmnets of mass numbers 80 and 120. If binding energy per nulceon for parent atom is 6.5MeV and for daughter nuceli is 7MeV and 8MeV, respectivley , then the energy released in the decay will be.
View SolutionConsider the nuclear reaction X200→A110+B80+Q. If the binding energy per nucleon for X, A and B are 7.4 MeV, 8.2 MeV and 8.1 MeV respectively, then the energy released in the reaction:
View SolutionA nucleus with mass number A =240 and BE/A = 7.6 Me V breaks into two fragments each of A =120 with BE/A =8.5 Me V .Calculate the released energy .
View SolutionDraw the graph showing thervariation of binding energy per nucleon with mass number. Give therason for the decrease of binding energy per nucleon for nuclei with high mass numbers.
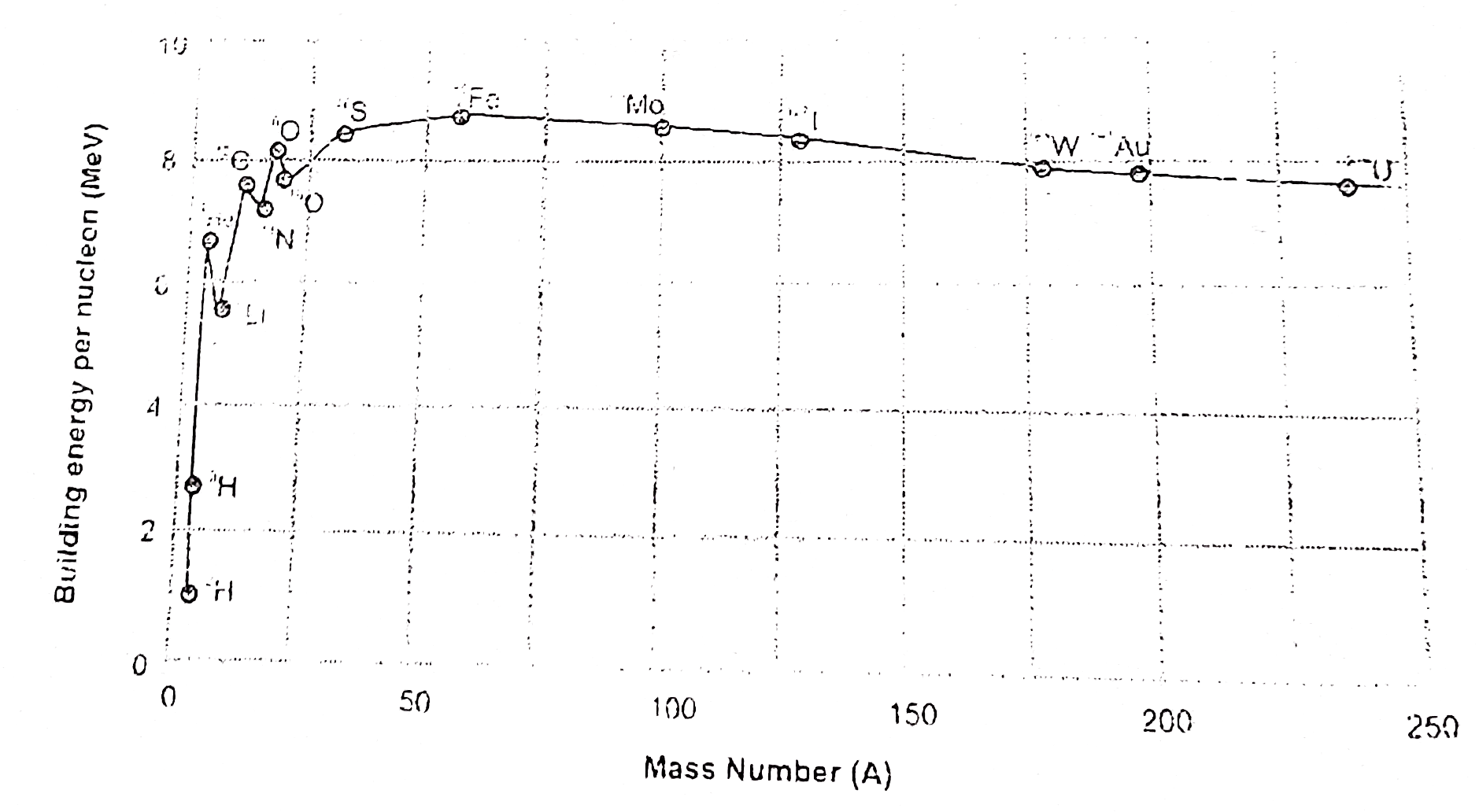
The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.View SolutionCalculate the binding energy per nucleon for C12 Masses of proton and neutron are 1.0078 and 1.0087, respectively.
(mu=931MeV)View Solution

