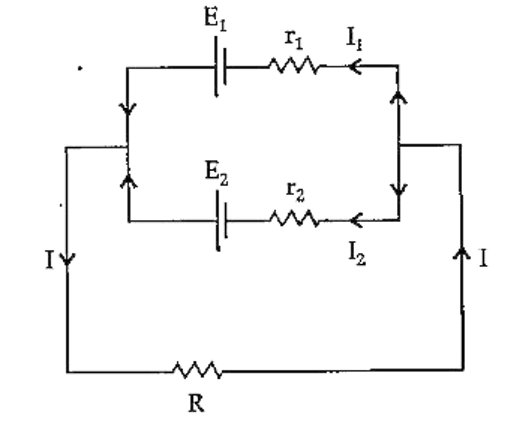
A student connects a cell of emf ε2 and internal resistance r2, with a cell of emf ε1 such that their combinationhas a net internal resistance less then r1. This combination in the connected across a resistance R. Draw a circuit of the 'set up' and obtain an expression for the current flowing through the resistance R
To solve the problem, we will follow these steps:
Step 1: Understand the Configuration
We have two cells connected in parallel, one with emf \( \epsilon_1 \) and internal resistance \( r_1 \), and the other with emf \( \epsilon_2 \) and internal resistance \( r_2 \). The goal is to find the current flowing through an external resistance \( R \) when these cells are connected.
Step 2: Draw the Circuit Diagram
The circuit diagram will look like this:
±−−(r1)−−−+||(ε1)(ε2)||±−−(r2)−−−+|R|GND
Step 3: Calculate the Equivalent EMF
When two cells are connected in parallel, the equivalent emf \( \epsilon \) is given by the formula:
\(
\epsilon = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}
\)
This formula accounts for the contributions of both cells and their internal resistances.
Step 4: Calculate the Equivalent Resistance
The equivalent internal resistance \( r \) for the two cells in parallel is given by:
\(
r = \frac{r_1 r_2}{r_1 + r_2}
\)
Step 5: Apply Ohm's Law to Find Current
The total current \( I \) flowing through the external resistance \( R \) can be calculated using Ohm's Law:
\(
I = \frac{\epsilon}{R + r}
\)
Substituting the expressions for \( \epsilon \) and \( r \):
\(
I = \frac{\frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}}{R + \frac{r_1 r_2}{r_1 + r_2}}
\)
Step 6: Simplify the Expression
To simplify the expression for \( I \):
1. The denominator can be simplified as follows:
\(
R + \frac{r_1 r_2}{r_1 + r_2} = \frac{(R + r_1 + r_2) (r_1 + r_2)}{r_1 + r_2}
\)
2. Thus, the current expression becomes:
\(
I = \frac{(\epsilon_1 r_2 + \epsilon_2 r_1)}{(R + r_1 + r_2)}
\)
Final Expression for Current
The final expression for the current flowing through the resistance \( R \) is:
\(
I = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{R(r_1 + r_2) + r_1 r_2}
\)
We have two cells connected in parallel, one with emf \( \epsilon_1 \) and internal resistance \( r_1 \), and the other with emf \( \epsilon_2 \) and internal resistance \( r_2 \). The goal is to find the current flowing through an external resistance \( R \) when these cells are connected.
The circuit diagram will look like this:
When two cells are connected in parallel, the equivalent emf \( \epsilon \) is given by the formula:
\epsilon = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}
\)
The equivalent internal resistance \( r \) for the two cells in parallel is given by:
r = \frac{r_1 r_2}{r_1 + r_2}
\)
The total current \( I \) flowing through the external resistance \( R \) can be calculated using Ohm's Law:
I = \frac{\epsilon}{R + r}
\)
I = \frac{\frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}}{R + \frac{r_1 r_2}{r_1 + r_2}}
\)
To simplify the expression for \( I \):
\(
R + \frac{r_1 r_2}{r_1 + r_2} = \frac{(R + r_1 + r_2) (r_1 + r_2)}{r_1 + r_2}
\)
\(
I = \frac{(\epsilon_1 r_2 + \epsilon_2 r_1)}{(R + r_1 + r_2)}
\)
The final expression for the current flowing through the resistance \( R \) is:
I = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{R(r_1 + r_2) + r_1 r_2}
\)
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
View SolutionFour identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View Solution
Knowledge Check
- Question 1 - Select One
In the series combination of n cells each cell having emf ε and internal resistance r. If three cells are wrongly connected, then total emf and internal resistance of this combination will be
Anε,(nr−3r)B(nε−2r),nrC(nε−4ε),nrD(nε−6ε),nr
Five cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
 View Solution
View Solutionn equal cell having emf E and internal resistance r, are connected in circuit of a resistance R. Same current flows in circuit either they connected in series or parallel, if:
View SolutionTwo identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
View Solution

