A parallel plate capacitor of capacitance C is charged to a potential V by a battery. Without disconnecting the battery, distance between the plates of capacitor is tripled and a dielectric medium of K = 10 is introduced between the plates of capacitor. Explain giving reasons how will the following be affected ?
(a) Capacitance of capacitor
(b) Charge on capacitor
(c ) Energy density of capacitor.
To solve the problem step by step, we will analyze the effects of tripling the distance between the plates of a capacitor and introducing a dielectric medium with a dielectric constant K=10.
Step 1: Calculate the New Capacitance
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0AD
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
When the distance D is tripled, the new distance D′ becomes:
D′=3D
When a dielectric medium with dielectric constant K=10 is introduced, the new capacitance C′ can be calculated as:
C′=Kε0AD′
Substituting D′:
C′=10ε0A3D
Since C=ε0AD, we can express C′ in terms of C:
C′=103C
Step 2: Calculate the New Charge on the Capacitor
The charge Q on a capacitor is given by:
Q=CV
Initially, the charge Q0 is:
Q0=CV
After introducing the dielectric and changing the capacitance, the new charge Q′ is:
Q′=C′V=(103C)V=103Q0
Step 3: Calculate the New Energy Density of the Capacitor
The energy density ρ of a capacitor is given by:
ρ=12Q2CA
Substituting Q=CV:
ρ=12CV2A
For the new energy density ρ′:
ρ′=12Q′2C′A
Substituting Q′=103Q0 and C′=103C:
ρ′=12(103Q0)2(103C)A
This simplifies to:
ρ′=121009Q20103CA=103Q202CA=103ρ0
However, we need to account for the dielectric:
ρ′=109ρ0
Summary of Effects
(a) The new capacitance C′ is 103C.
(b) The new charge Q′ is 103Q0.
(c) The new energy density ρ′ is 109ρ0.
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0AD
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
D′=3D
C′=Kε0AD′
Substituting D′:
C′=10ε0A3D
C′=103C
The charge Q on a capacitor is given by:
Q=CV
Initially, the charge Q0 is:
Q0=CV
Q′=C′V=(103C)V=103Q0
The energy density ρ of a capacitor is given by:
ρ=12Q2CA
Substituting Q=CV:
ρ=12CV2A
ρ′=12Q′2C′A
Substituting Q′=103Q0 and C′=103C:
ρ′=12(103Q0)2(103C)A
This simplifies to:
ρ′=121009Q20103CA=103Q202CA=103ρ0
ρ′=109ρ0
(a) The new capacitance C′ is 103C.
(b) The new charge Q′ is 103Q0.
(c) The new energy density ρ′ is 109ρ0.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
11 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-B
52 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A parallel plate capacitor is charged to a potential difference of 10 volts. After disconnecting the battery, distance between the plates of capacitor is decreased by using nonconducting handles. The potential difference between the plates will
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View Solution
Knowledge Check
A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
AincreasesBdecreaseCdoes not chargeDbecomes zeroAs the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
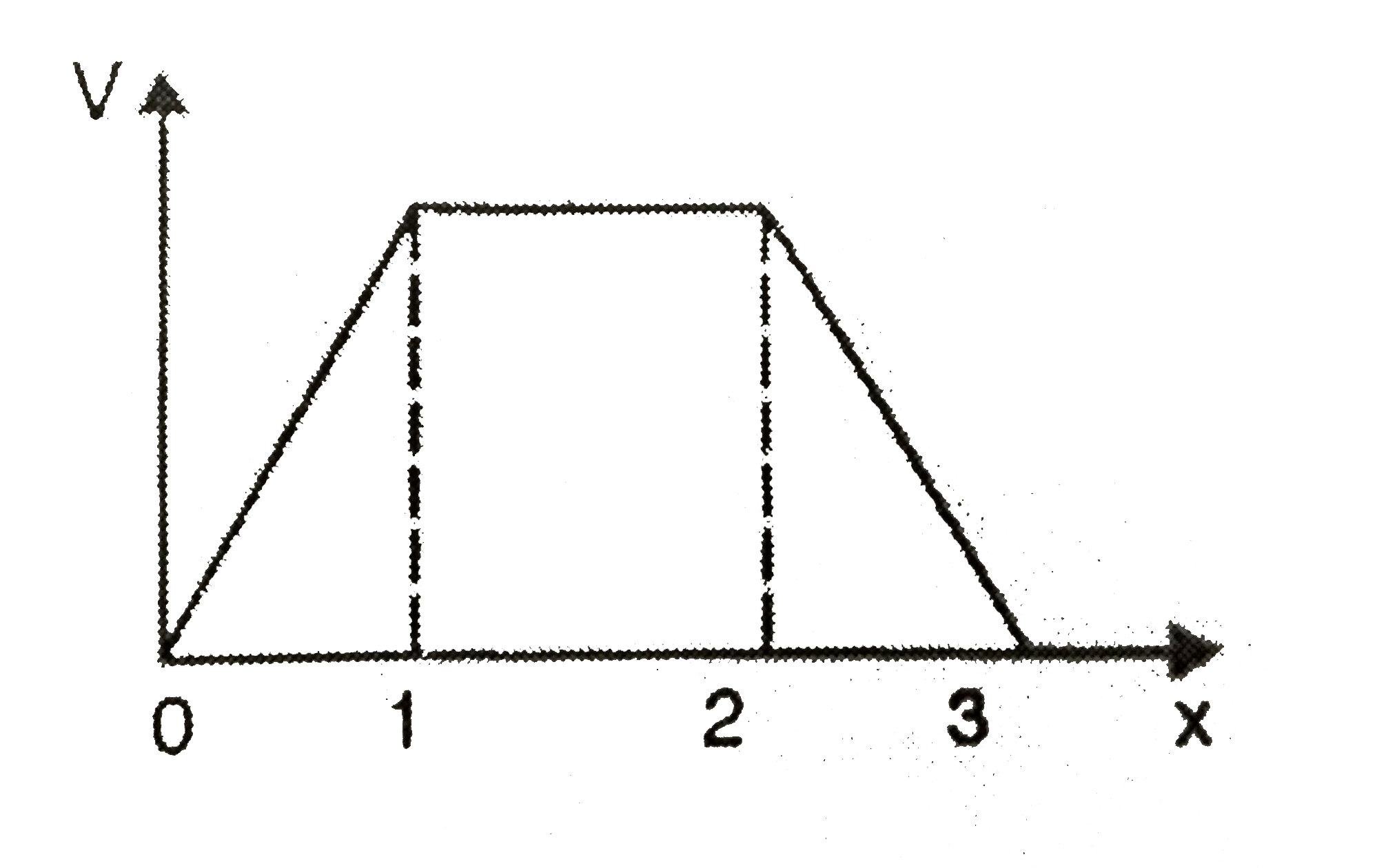
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionTwo parallel conducting plates of a capacitor of capacitance C containing charges Q and -2Q at a distance d apart. Find out potential difference between the plates of capacitors.
View SolutionA parallel plate capacitor of plate area A and plates separation distance d is charged by applying a potential V0 between the plates. The dielectric constant of the medium between the plates is K. What is the uniform electric field E between the plates of the capacitor ?
View SolutionA parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
View Solution