Answer the following:
(a) State Biot - Savart's law and express this law in the vector form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
Step-by-Step Solution:
1. Definition of Biot-Savart's Law:
Biot-Savart's law states that the magnetic field B produced at a point in space by a small segment of current-carrying wire is directly proportional to the current I, the length of the current element dl, and the sine of the angle θ between the current element and the line connecting the element to the point where the magnetic field is being calculated. It is inversely proportional to the square of the distance r from the current element to the point.
Mathematically, this can be expressed as:
dB∝Idlsinθr2
2. Vector Form of Biot-Savart's Law:
To express this law in vector form, we introduce a proportionality constant μ04π, where μ0 is the permeability of free space. The vector form of Biot-Savart's law is given by:
dB=μ04πIdl×rr3
where r is the position vector from the current element to the point where the magnetic field is being calculated.
(b) Finding the Net Magnetic Field at the Center of the Coils
1. Magnetic Field due to Coil P:
- For coil P carrying current I1=1A:
B1=μ0I12R^k
2. Magnetic Field due to Coil Q:
- For coil Q carrying current I2=√3A:
B2=μ0I22R^i=μ0√32R^i
3. Magnitude of the Net Magnetic Field:
- The net magnetic field B at the center of the coils can be calculated using the Pythagorean theorem since the two magnetic fields are perpendicular to each other:
B=√B21+B22
Substituting the values:
B=
⎷(μ02R)2+(μ0√32R)2
B=√μ204R2+3μ204R2=√4μ204R2=μ0R
4. Direction of the Net Magnetic Field:
- The direction of the net magnetic field can be found using the tangent of the angle θ:
tanθ=B2B1=μ0√32Rμ02R=√3
- Therefore, θ=60∘ with respect to the direction of B1 (which is along the z-axis).
Final Answer:
- Biot-Savart's Law in Vector Form:
dB=μ04πIdl×rr3
- Magnitude of the Net Magnetic Field:
B=μ0R
- Direction of the Net Magnetic Field:
60∘ with respect to the z-axis.
Biot-Savart's law states that the magnetic field B produced at a point in space by a small segment of current-carrying wire is directly proportional to the current I, the length of the current element dl, and the sine of the angle θ between the current element and the line connecting the element to the point where the magnetic field is being calculated. It is inversely proportional to the square of the distance r from the current element to the point.
dB∝Idlsinθr2
To express this law in vector form, we introduce a proportionality constant μ04π, where μ0 is the permeability of free space. The vector form of Biot-Savart's law is given by:
dB=μ04πIdl×rr3
where r is the position vector from the current element to the point where the magnetic field is being calculated.
- For coil P carrying current I1=1A:
B1=μ0I12R^k
- For coil Q carrying current I2=√3A:
B2=μ0I22R^i=μ0√32R^i
- The net magnetic field B at the center of the coils can be calculated using the Pythagorean theorem since the two magnetic fields are perpendicular to each other:
B=√B21+B22
Substituting the values:
B=
⎷(μ02R)2+(μ0√32R)2
B=√μ204R2+3μ204R2=√4μ204R2=μ0R
- The direction of the net magnetic field can be found using the tangent of the angle θ:
tanθ=B2B1=μ0√32Rμ02R=√3
- Therefore, θ=60∘ with respect to the direction of B1 (which is along the z-axis).
- Biot-Savart's Law in Vector Form:
dB=μ04πIdl×rr3
- Magnitude of the Net Magnetic Field:
B=μ0R
- Direction of the Net Magnetic Field:
60∘ with respect to the z-axis.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C
50 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
11 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-A
28 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
State Biot-Savart law.
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
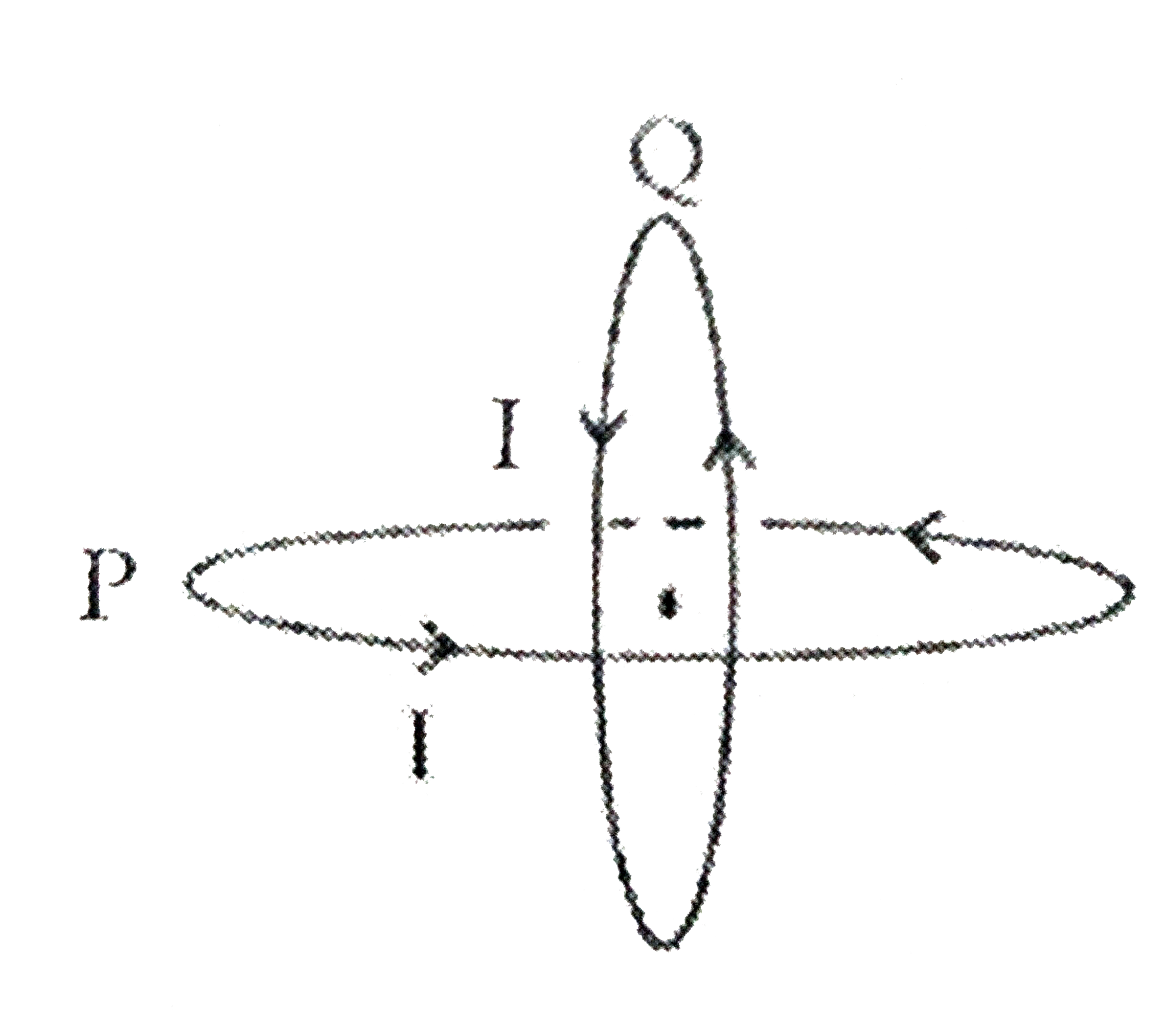
View Solution
Knowledge Check
The Biot Savart.s Law in vector form is :
A−→δB=μ04π.dI(→I×→r)r3B−→δB=μ04π.I(−→dI×→r)r2C−→δB=μ04π.I(→r×→dl)r3D−→δB=μ04π.I(→dl×→r)r
Two very small identical circular loops (1)and(2) carrying equal currents I are placed vertically (w.r.t. the plane of the paper) with their geometrical axes perpendicualr to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at point O.
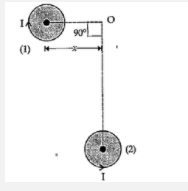
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes are perpendicular to each other, what would be the magnitude of the magnetic field B at the centre ?
View SolutionBiot Savart law of magnetism is analogous to:
View SolutionTwo circular coils A and B of radius 5√2cm amd 5cm respectively current 5amp and 5√2Amp respectively The plane of B is perpendicular to plane of A their centres coincide Find the magnetic field at the centre .
View SolutionTwo circular coils P & Q are coaxially & carry currents I1 and I2 respectively (all direction are w.r.t. the observer)

View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View Solution