A charge , is uniformaly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a point distant r form the centre of the spehre where :
(i) and
To solve the problem of finding the electric field due to a uniformly distributed charge +Q within a sphere of radius R at a point a distance r from the center of the sphere, we will analyze two cases:
Case (i): 0<r<R
1. Identify the Charge Density:
The charge density ρ can be calculated using the formula:
ρ=QVolume of the sphere=Q43πR3
2. Apply Gauss's Law:
To find the electric field E at a distance r from the center (where r<R), we consider a Gaussian surface which is a sphere of radius r. According to Gauss's Law:
∮E⋅dA=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
3. Calculate the Enclosed Charge:
The enclosed charge Qenc within the Gaussian surface of radius r is given by:
Qenc=ρ⋅Volume of the Gaussian surface=ρ⋅43πr3=Q43πR3⋅43πr3=Q⋅r3R3
4. Substitute into Gauss's Law:
The left side of Gauss's Law becomes:
E⋅4πr2
Thus, we have:
E⋅4πr2=Q⋅r3R3ϵ0
5. Solve for Electric Field E:
Rearranging gives:
E=Q4πϵ0⋅rR3
The direction of the electric field is radially outward, denoted as ^r.
Case (ii): r>R
1. Apply Gauss's Law Again:
For r>R, we again use Gauss's Law with a Gaussian surface of radius r:
∮E⋅dA=Qencϵ0
2. Determine the Enclosed Charge:
Here, the entire charge Q is enclosed:
Qenc=Q
3. Substitute into Gauss's Law:
The left side becomes:
E⋅4πr2
Thus, we have:
E⋅4πr2=Qϵ0
4. Solve for Electric Field E:
Rearranging gives:
E=Q4πϵ0r2
The direction of the electric field is also radially outward, denoted as ^r.
Summary of Results:
- For 0<r<R:
E=Q4πϵ0⋅rR3^r
- For r>R:
E=Q4πϵ0r2^r
The charge density ρ can be calculated using the formula:
ρ=QVolume of the sphere=Q43πR3
To find the electric field E at a distance r from the center (where r<R), we consider a Gaussian surface which is a sphere of radius r. According to Gauss's Law:
∮E⋅dA=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
The enclosed charge Qenc within the Gaussian surface of radius r is given by:
Qenc=ρ⋅Volume of the Gaussian surface=ρ⋅43πr3=Q43πR3⋅43πr3=Q⋅r3R3
The left side of Gauss's Law becomes:
E⋅4πr2
Thus, we have:
E⋅4πr2=Q⋅r3R3ϵ0
Rearranging gives:
E=Q4πϵ0⋅rR3
The direction of the electric field is radially outward, denoted as ^r.
For r>R, we again use Gauss's Law with a Gaussian surface of radius r:
∮E⋅dA=Qencϵ0
Here, the entire charge Q is enclosed:
Qenc=Q
The left side becomes:
E⋅4πr2
Thus, we have:
E⋅4πr2=Qϵ0
Rearranging gives:
E=Q4πϵ0r2
The direction of the electric field is also radially outward, denoted as ^r.
- For 0<r<R:
E=Q4πϵ0⋅rR3^r
- For r>R:
E=Q4πϵ0r2^r
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]11videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-B52videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.
 View Solution
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).
 View Solution
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionA solid sphere of radius R has a charge +2Q. A hollow spherical concentric with the first sphere that has net charge -Q.
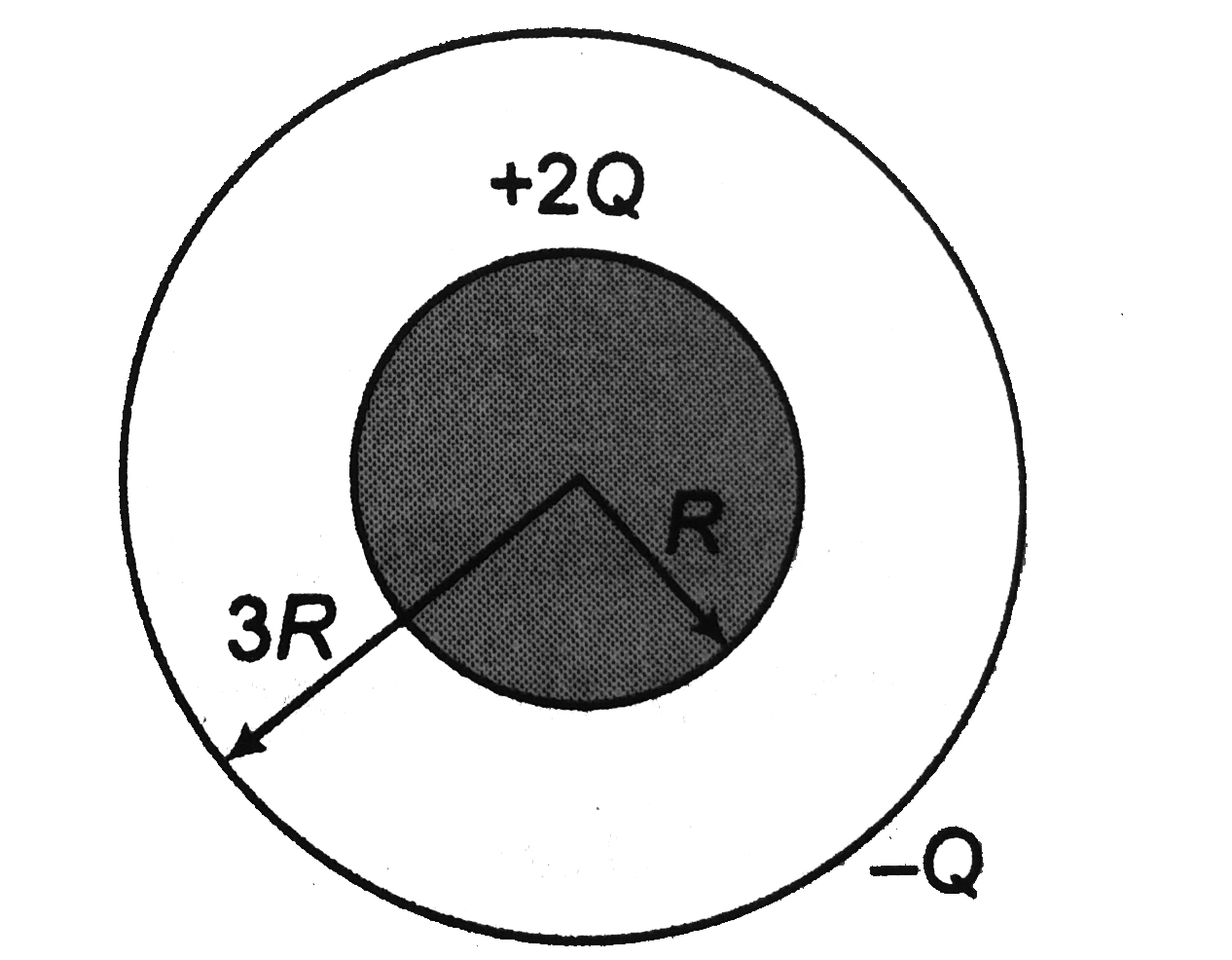
(a) Find the electric field between the spheres at a distance r from the centre of the inner sphere. [R<r<3R]
(b) Calculate the potential difference between the spheres.
(c) What would be the final distribution of charges, if a conducting wire joins the spheres?
(d) Instead of (c), if the inner sphere is earthed, what is the charge on it?View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
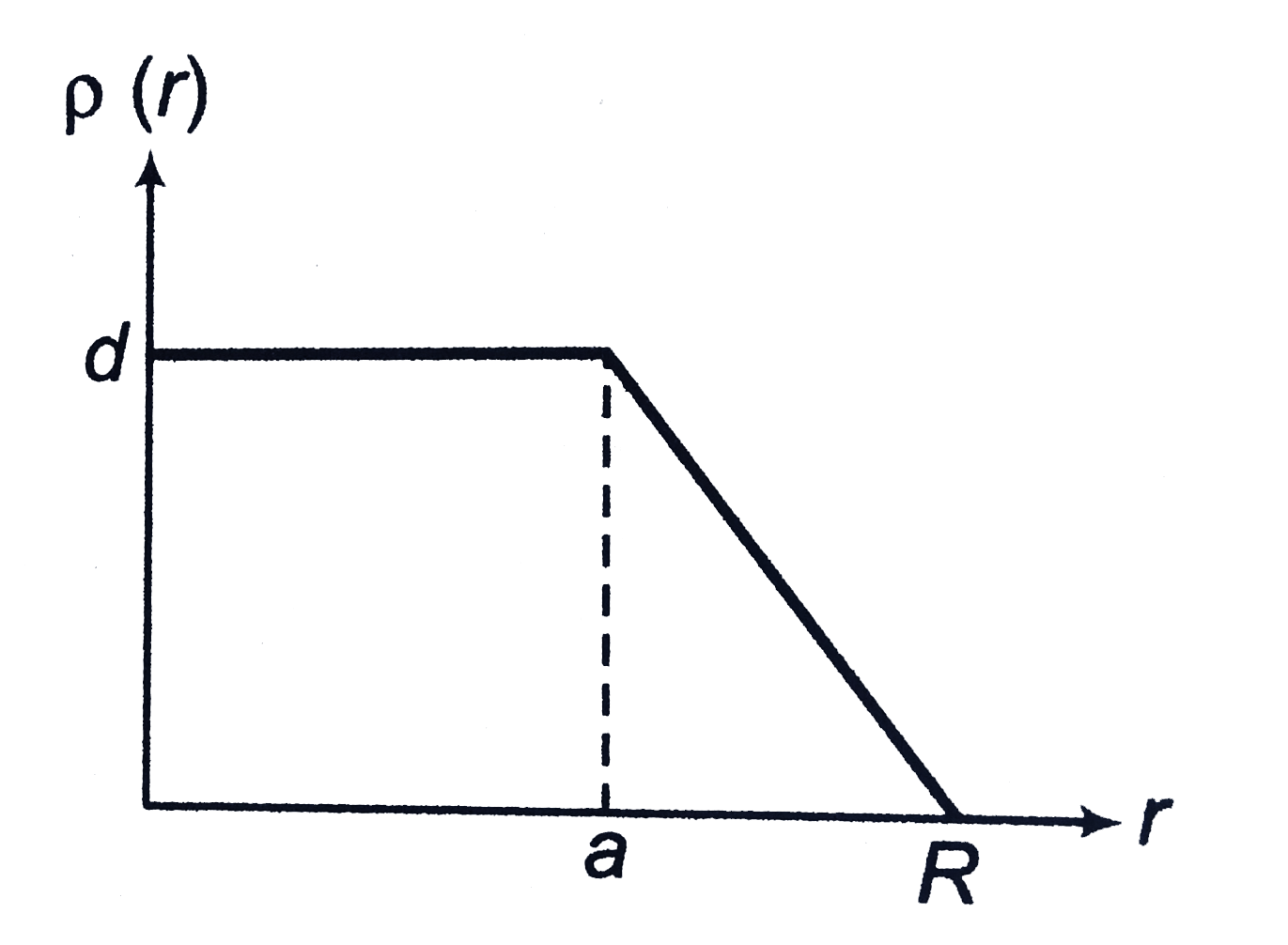
The electric field within the nucleus is generaly observed to be linearly dependent on r. This impliesView Solution

