Combination of Bulbs
To solve the question regarding the combination of bulbs, we will analyze both series and parallel combinations step by step.
1. Understanding Series Combination:
- In a series combination, the positive terminal of the first bulb is connected to the negative terminal of the second bulb. This pattern continues for additional bulbs.
- For example, if we have three bulbs (B1, B2, B3), the connections would be:
- Positive of B1 to the positive terminal of the battery.
- Negative of B1 to the positive of B2.
- Negative of B2 to the positive of B3.
- Negative of B3 to the negative terminal of the battery.
- Current in Series: The same current flows through all the bulbs. This means that the current (I) is constant across each bulb.
2. Understanding Parallel Combination:
- In a parallel combination, all the positive terminals of the bulbs are connected together, and all the negative terminals are connected together.
- For example, with three bulbs (B1, B2, B3), the connections would be:
- Positive of B1, B2, and B3 are all connected to the positive terminal of the battery.
- Negative of B1, B2, and B3 are all connected to the negative terminal of the battery.
- Voltage in Parallel: The voltage across each bulb is the same and equal to the voltage of the battery (V).
3. Key Differences:
- In series:
- Current (I) is the same through all bulbs.
- Total resistance (R_total) is the sum of individual resistances (R_total = R1 + R2 + R3).
- In parallel:
- Voltage (V) is the same across all bulbs.
- Total resistance (R_total) can be calculated using the formula:
1Rtotal=1R1+1R2+1R3
Summary:
- Series Combination: Same current through all bulbs, total resistance is the sum of individual resistances.
- Parallel Combination: Same voltage across all bulbs, total resistance is calculated using the reciprocal formula.
- In a series combination, the positive terminal of the first bulb is connected to the negative terminal of the second bulb. This pattern continues for additional bulbs.
- For example, if we have three bulbs (B1, B2, B3), the connections would be:
- Positive of B1 to the positive terminal of the battery.
- Negative of B1 to the positive of B2.
- Negative of B2 to the positive of B3.
- Negative of B3 to the negative terminal of the battery.
- Current in Series: The same current flows through all the bulbs. This means that the current (I) is constant across each bulb.
- In a parallel combination, all the positive terminals of the bulbs are connected together, and all the negative terminals are connected together.
- For example, with three bulbs (B1, B2, B3), the connections would be:
- Positive of B1, B2, and B3 are all connected to the positive terminal of the battery.
- Negative of B1, B2, and B3 are all connected to the negative terminal of the battery.
- Voltage in Parallel: The voltage across each bulb is the same and equal to the voltage of the battery (V).
- In series:
- Current (I) is the same through all bulbs.
- Total resistance (R_total) is the sum of individual resistances (R_total = R1 + R2 + R3).
- In parallel:
- Voltage (V) is the same across all bulbs.
- Total resistance (R_total) can be calculated using the formula:
1Rtotal=1R1+1R2+1R3
- Series Combination: Same current through all bulbs, total resistance is the sum of individual resistances.
- Parallel Combination: Same voltage across all bulbs, total resistance is calculated using the reciprocal formula.
Topper's Solved these Questions
Similar Questions
Assertion: In series combination of electric bulbs th ebulb of lower power emits more light than that of higher power bulb.
Reason: The lower power bulb in series gets more current than the higher power bulb.
View SolutionAssertion: Two electric bulbs of 50 and 100W. Are given. When connected in sereis 50W bulb glows more but when connected parallel 100 W bulb glows more.
Reason : In series combination, power is directly proportional to the resistance of circuit. but in parallel comb ination, power is inversely proportional to the resistance of the circuit.
View Solution
Knowledge Check
A Box Contains 100 Bulbs Out Of Which 10 Are Defective A Sample Of 5 Bulbs Is Drawn The Probability That None Is Defective Is
A(12)5B910C(910)5D(110)5
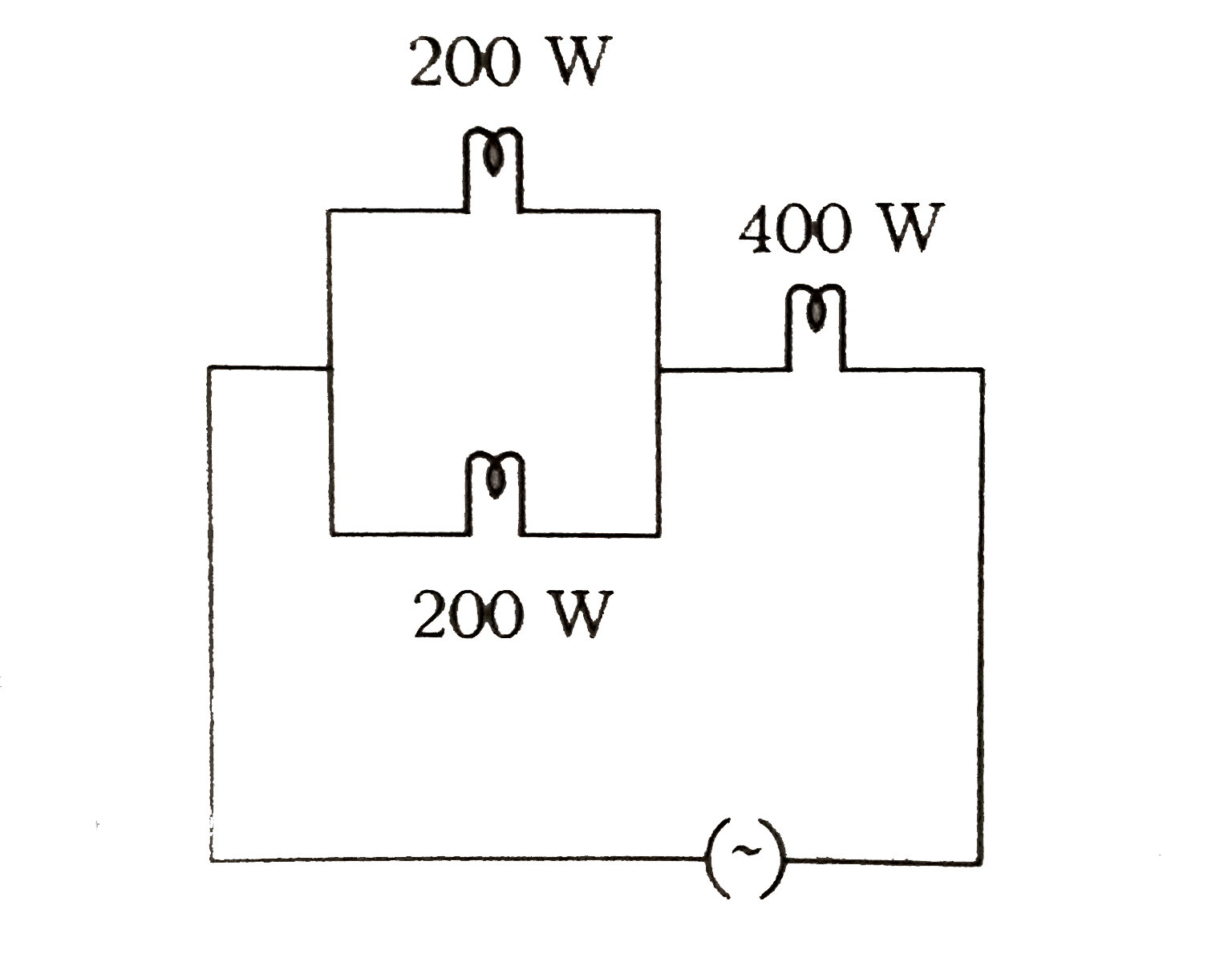
Three electric bulbs of 200 W and 400 W are shown in figure. The resultant power of the combination if rated voltage is applied across the combination is (50x) Watt. Find value of x.

View SolutionA 50 W bulb is in series with a room heater and the combination is conneted across the mains. To get max, heater output, the 50 W bulb should be replaced by :
View SolutionAn electric bulb rated 220Vand60W is connected in series with another electric bulb rated 220Vand40W. The combination is connected across a source of emf220V. Which bulb will glow more?
View SolutionThree electric bulbs of 200 W, 200 W and 400 W are connected as shown in figure. The resultant power of the combination is
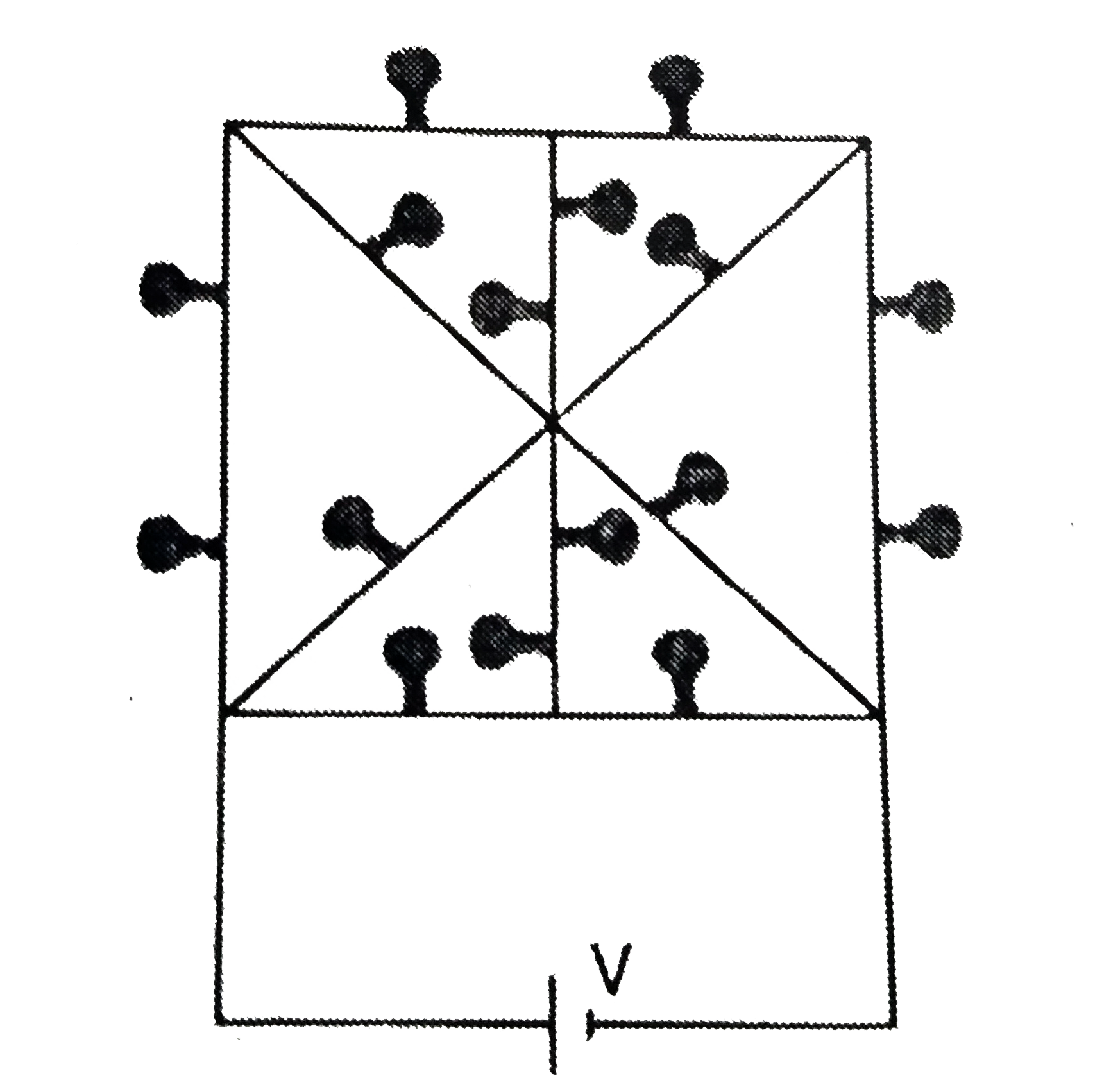
View SolutionStandard rating of each bulb is P, V. If total power consumption by combination is 3XP5 then calculate 'X'.
View SolutionTwo 220 V,100 W bulbs are connected first in series and then in parallel. Each time the combination is connected to a 220 V AC supply line. The power drawn by the combination in each case respectively will be :
View SolutionTwo 220 volt, 200 W bulbs are connected first in series and then in parallel. Each time the combination is connected to 220 V. The ratio of power drawn by the combination in respective cases is
View Solution
