Combination of Inductors
To solve the problem of finding the total inductance in a combination of inductors connected in series, we can follow these steps:
1. Understanding Series Connection:
In a series connection of inductors, the same current flows through each inductor. Let’s denote the inductors as L1, L2, L3, and L4.
2. Current in Series:
Since the inductors are in series, the current (I) through each inductor is the same. Therefore, we can say:
I=I1=I2=I3=I4
3. Voltage Across Each Inductor:
The voltage across each inductor can be expressed using the formula:
V=Ldidt
Therefore, the voltage across each inductor can be written as:
V1=L1didt,V2=L2didt,V3=L3didt,V4=L4didt
4. Total Voltage in Series:
The total voltage (V) across the series combination of inductors is the sum of the individual voltages:
V=V1+V2+V3+V4
Substituting the expressions for the voltages, we get:
V=L1didt+L2didt+L3didt+L4didt
5. Factoring Out Common Terms:
We can factor out didt from the equation:
V=(L1+L2+L3+L4)didt
6. Total Inductance:
From the above equation, we can identify the total inductance (L_total) of the series combination:
Ltotal=L1+L2+L3+L4
Final Result:
The total inductance of inductors connected in series is given by:
Ltotal=L1+L2+L3+L4
In a series connection of inductors, the same current flows through each inductor. Let’s denote the inductors as L1, L2, L3, and L4.
Since the inductors are in series, the current (I) through each inductor is the same. Therefore, we can say:
I=I1=I2=I3=I4
The voltage across each inductor can be expressed using the formula:
V=Ldidt
Therefore, the voltage across each inductor can be written as:
V1=L1didt,V2=L2didt,V3=L3didt,V4=L4didt
The total voltage (V) across the series combination of inductors is the sum of the individual voltages:
V=V1+V2+V3+V4
Substituting the expressions for the voltages, we get:
V=L1didt+L2didt+L3didt+L4didt
We can factor out didt from the equation:
V=(L1+L2+L3+L4)didt
From the above equation, we can identify the total inductance (L_total) of the series combination:
Ltotal=L1+L2+L3+L4
The total inductance of inductors connected in series is given by:
Ltotal=L1+L2+L3+L4
Topper's Solved these Questions
Similar Questions
An a.c. voltage of (V=100sinωt) volt is connected across the parallel combination of inductor and capacitor having(XL=5Ω) and (X_C = 10 Omega) then current supplied by source is (in ampere)
View SolutionCombination of Bulbs
View SolutionCombination of Cells
View SolutionAn ideal choke takes a current of 8A when connected to an a.c. source of 100 volt and 50Hz. A pure resistor under the same conditions takes a current of 10A. If two are connected in series to an a.c. supply of 100V and 40Hz, then the current in the series combination of above resistor and inductor is
View SolutionAn ideal choke takes a current of 10 A when connected to an ac supply of 125 V and 50 Hz. A pure resistor under the same conditions takes a current of 12.5 A. If the two are connected to an ac supply of 100 V and 40 Hz, then the current in series combination of above resistor and inductor is
View SolutionA light bulb and an inductor coil are connected to an ac source through a key as shown in figure below. The key is closed and after sometime an iron rod is inserted into interior of inductor. The glow of light bulb
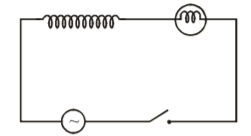
View SolutionCombination of Resistance
View SolutionA sinusoidal voltage Vsin(at) is applied across a series combination of resistance R and inductor L. The amplitude of the current in the circuit is
View SolutionAn AC voltage is applied acrss a series combination of L and R. If the voltage drop across the resistor and inductor are 20V and 15V respectiely, then applied peak voltage is
View SolutionAn A.C. generator generating an e.m.f. of ε=300sin(100πt)V is connected to a series combination of 16μF capacitor, 1H inductor and 100Ω resistor. Calculate
Impedance of the circuit at the given frequency
View Solution

