An ac source of emf V=V0sinωt is connected to a capacitor of capacitance C. Deduce the expression for the current (I) flowing in it. Plot the graph of (i) Vvs.ωt,and (ii) Ivs.ωt
To derive the expression for the current flowing in a capacitor connected to an AC source, we can follow these steps:
Step 1: Understand the given information
We have an AC voltage source given by:
V(t)=V0sin(ωt)
where V0 is the peak voltage, ω is the angular frequency, and t is time.
Step 2: Relate voltage and charge
The voltage across a capacitor is related to the charge Q on the capacitor by the formula:
V=QC
where C is the capacitance of the capacitor.
Step 3: Express charge in terms of voltage
From the voltage equation, we can express the charge Q as:
Q=C⋅V=C⋅V0sin(ωt)
Step 4: Find the current
The current I flowing through the capacitor is defined as the rate of change of charge with respect to time:
I=dQdt
Step 5: Differentiate the charge with respect to time
Substituting Q=C⋅V0sin(ωt) into the current equation, we get:
I=ddt(C⋅V0sin(ωt))
Using the chain rule, we differentiate:
I=C⋅V0⋅ddt(sin(ωt))
I=C⋅V0⋅ωcos(ωt)
Step 6: Express current in terms of peak current
We can express the current in terms of its peak value I0:
I0=C⋅V0⋅ω
Thus, the current can be rewritten as:
I=I0cos(ωt)
Step 7: Relate the current to the voltage phase
Since cos(ωt) can be expressed as a sine function with a phase shift:
I=I0sin(ωt+π2)
This indicates that the current leads the voltage by 90∘ (or π2 radians).
Final Expression
The final expression for the current flowing in the capacitor is:
I=I0sin(ωt+π2)
Graphs
1. Graph of V vs. ωt:
- This will be a standard sine wave starting from the origin, oscillating between −V0 and V0.
2. Graph of I vs. ωt:
- This will also be a sine wave, but it will reach its maximum value I0 a quarter period (or π2 radians) earlier than the voltage wave.
We have an AC voltage source given by:
V(t)=V0sin(ωt)
where V0 is the peak voltage, ω is the angular frequency, and t is time.
The voltage across a capacitor is related to the charge Q on the capacitor by the formula:
V=QC
where C is the capacitance of the capacitor.
From the voltage equation, we can express the charge Q as:
Q=C⋅V=C⋅V0sin(ωt)
The current I flowing through the capacitor is defined as the rate of change of charge with respect to time:
I=dQdt
Substituting Q=C⋅V0sin(ωt) into the current equation, we get:
I=ddt(C⋅V0sin(ωt))
Using the chain rule, we differentiate:
I=C⋅V0⋅ddt(sin(ωt))
I=C⋅V0⋅ωcos(ωt)
We can express the current in terms of its peak value I0:
I0=C⋅V0⋅ω
Thus, the current can be rewritten as:
I=I0cos(ωt)
Since cos(ωt) can be expressed as a sine function with a phase shift:
I=I0sin(ωt+π2)
This indicates that the current leads the voltage by 90∘ (or π2 radians).
The final expression for the current flowing in the capacitor is:
I=I0sin(ωt+π2)
1. Graph of V vs. ωt:
- This will be a standard sine wave starting from the origin, oscillating between −V0 and V0.
- This will also be a sine wave, but it will reach its maximum value I0 a quarter period (or π2 radians) earlier than the voltage wave.
Similar Questions
Knowledge Check
A 5μF capacitor is connected to a 200 V, 100 Hz ac source. The capacitive reactance is
A212ΩB312ΩC318ΩD412Ω
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionAn AC source is connected to a capacitor. The current in the current is I. Now a dielectric slab is inserted into the capacitor , then the new current is
View SolutionAn AC voltage source V=V0sinωt is connected across resistance R and capacitance C as shown in figure. It is given that ωC=1R. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
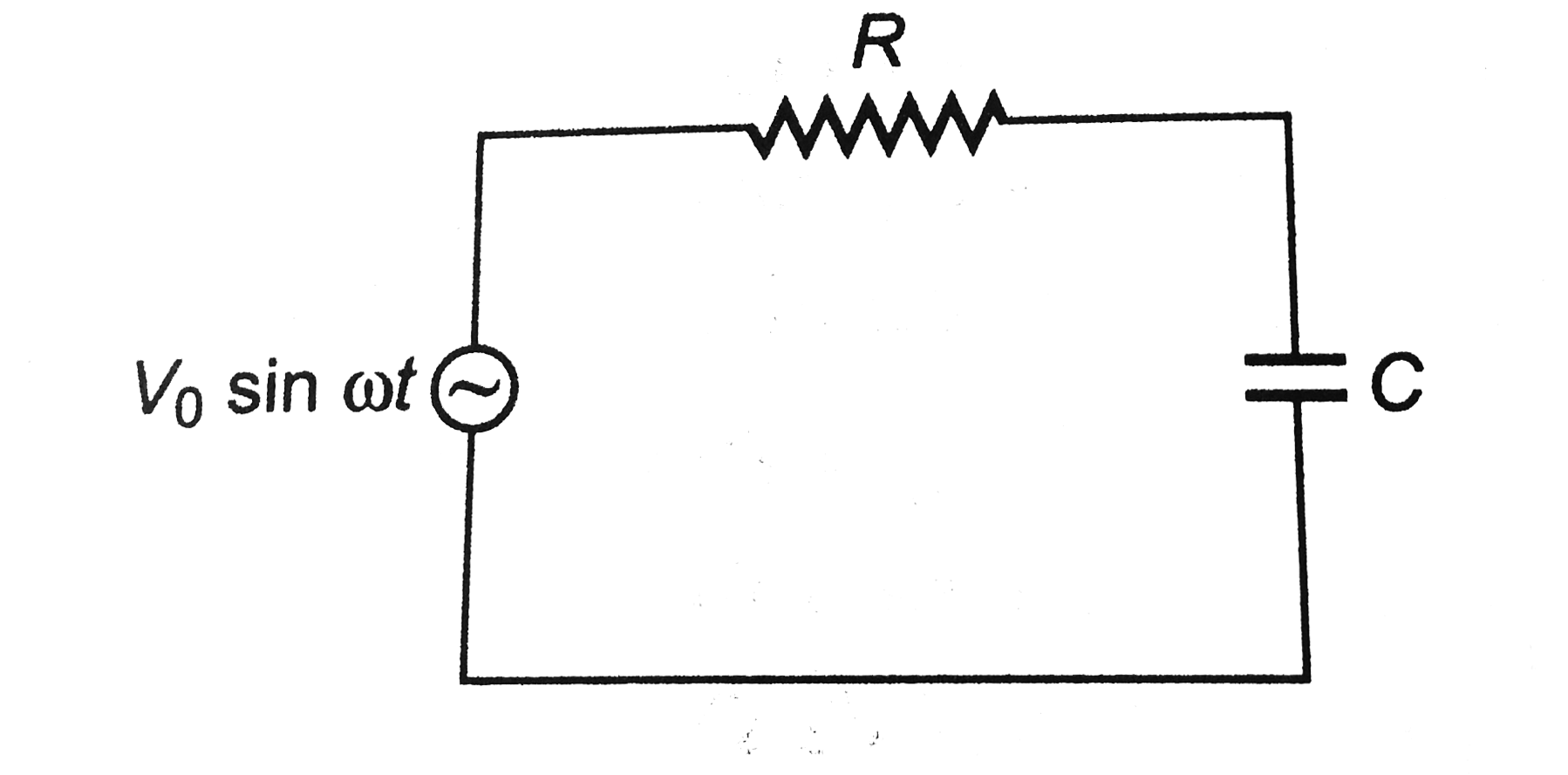 .
.
View SolutionAn inductor coil joined to a 6V battery draws a steady current of 12A. This coil is connected to a capacitor and an AC source of rms voltage 6V in series. If the current in the circuit is in phase with the emf, find the rms current.
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionA 100W bulb is connected to an AC source of 220V, 50Hz. Then the current flowing through the bulb is
View SolutionA square loop of side 'a' with a capacitor of capacitance C is located between two current carrying long parallel wires as shown. The value of I in the wires in given as I=(I0)sinωt.
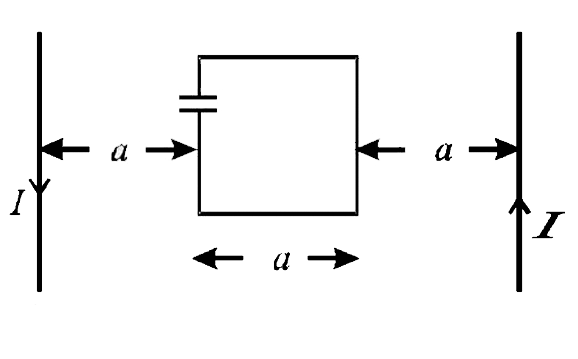
(a) Calculate maximum current in the square loop.
(b) Draw a graph between charges on the upper plates of the capacitor vs time.
View Solution
