In a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that
To solve the problem, we need to show that triangle PAD is isosceles and that ∠CAD=12(∠PBA−∠PAB). Let's break this down step by step.
Step 1: Understand the Given Information
- Given:
- PA is a tangent to the circle.
- PBC is a secant.
- AD bisects angle BAC.
Step 2: Define Angles
Let:
- ∠CAB=2x
- ∠PAB=y
From this, we can deduce:
- ∠ABC=x (since AD bisects ∠CAB)
- Therefore, ∠CBA=x as well.
Step 3: Analyze the Angles
Since PA is a tangent and PB is a secant, we can use the property of tangents and secants:
- ∠BAP=∠BCA=y
Step 4: Exterior Angle of Triangle
Now, consider triangle ABC:
- The exterior angle ∠ADP can be expressed as:
∠ADP=∠CAB+∠ABC=2x+x=3x
Step 5: Angles in Triangle PAD
In triangle PAD:
- ∠PAD=∠DAB+∠PAB=x+y (from the definitions of angles)
- Therefore, we have:
∠PAD=x+y
Step 6: Show Triangle PAD is Isosceles
Since ∠PAD=∠ADP:
- From the previous steps, we have:
∠PAD=∠ADP=x+y
Thus, triangle PAD is isosceles because two of its angles are equal.
Step 7: Prove the Angle Relationship
Now, we need to show:
∠CAD=12(∠PBA−∠PAB)
Using the angles defined:
- ∠PBA=2x+y (since it is the sum of the angles in triangle ABC)
- ∠PAB=y
Now substituting into the equation:
∠CAD=12((2x+y)−y)=12(2x)=x
Conclusion
Thus, we have shown:
1. Triangle PAD is isosceles.
2. ∠CAD=12(∠PBA−∠PAB).
- Given:
- PA is a tangent to the circle.
- PBC is a secant.
- AD bisects angle BAC.
Let:
- ∠CAB=2x
- ∠PAB=y
- ∠ABC=x (since AD bisects ∠CAB)
- Therefore, ∠CBA=x as well.
Since PA is a tangent and PB is a secant, we can use the property of tangents and secants:
- ∠BAP=∠BCA=y
Now, consider triangle ABC:
- The exterior angle ∠ADP can be expressed as:
∠ADP=∠CAB+∠ABC=2x+x=3x
In triangle PAD:
- ∠PAD=∠DAB+∠PAB=x+y (from the definitions of angles)
- Therefore, we have:
∠PAD=x+y
Since ∠PAD=∠ADP:
- From the previous steps, we have:
∠PAD=∠ADP=x+y
Thus, triangle PAD is isosceles because two of its angles are equal.
Now, we need to show:
∠CAD=12(∠PBA−∠PAB)
- ∠PBA=2x+y (since it is the sum of the angles in triangle ABC)
- ∠PAB=y
∠CAD=12((2x+y)−y)=12(2x)=x
Thus, we have shown:
1. Triangle PAD is isosceles.
2. ∠CAD=12(∠PBA−∠PAB).
Topper's Solved these Questions
Similar Questions
In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
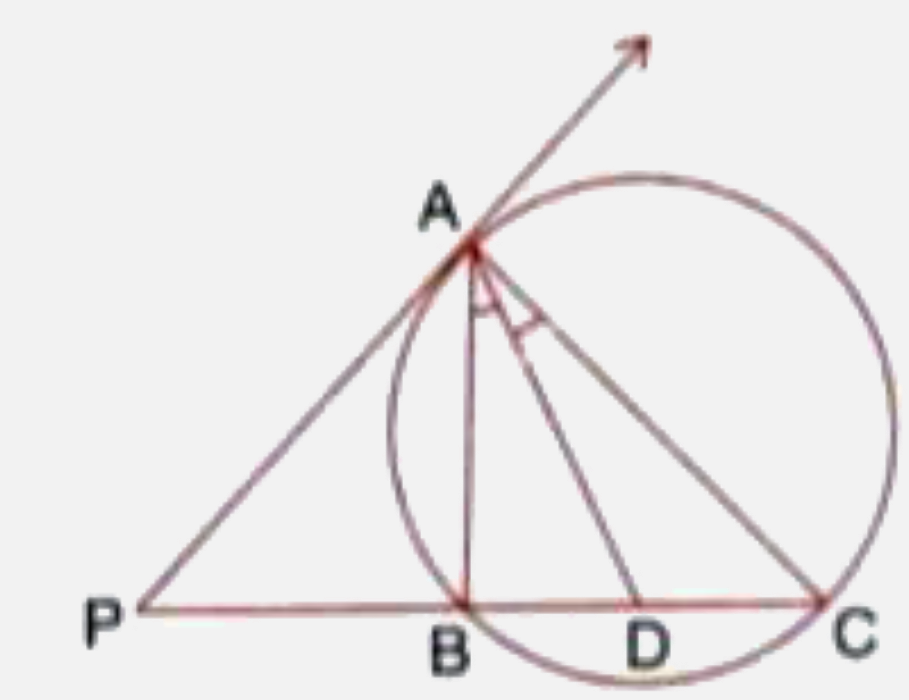
∠CAD=12[∠PBA−∠PAB]
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
View SolutionIn a triangle ABC, AB = AC. Show that the altitude AD is median also.
View SolutionIn a triangle ABC, side AC is greater than side AB and point D lies on side BC such that AD bisects angle BAC. Show that:
∠ADB is acute.
View SolutionIn a triangle ABC, if acosA=bcosB, show that the triangle is either isosceles or right angled.
View SolutionInΔABC,AB=ACandD is a piont in side BC such that AD bisect angle BAC.
Show that AD is perpendicular bisector of side BC.
View SolutionIf A, B, C are the angles of a triangle ABC and if cosA=sinB2sinC, show that the triangle is isosceles.
View SolutionIn a triangle ABC , if cosA=sinB2sinC , show that the triangle is isosceles.
View SolutionIn a ΔABC, D is the mid point of side AC such that BD =12 AC. Show that ∠ABC is a right angle.
View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View Solution
