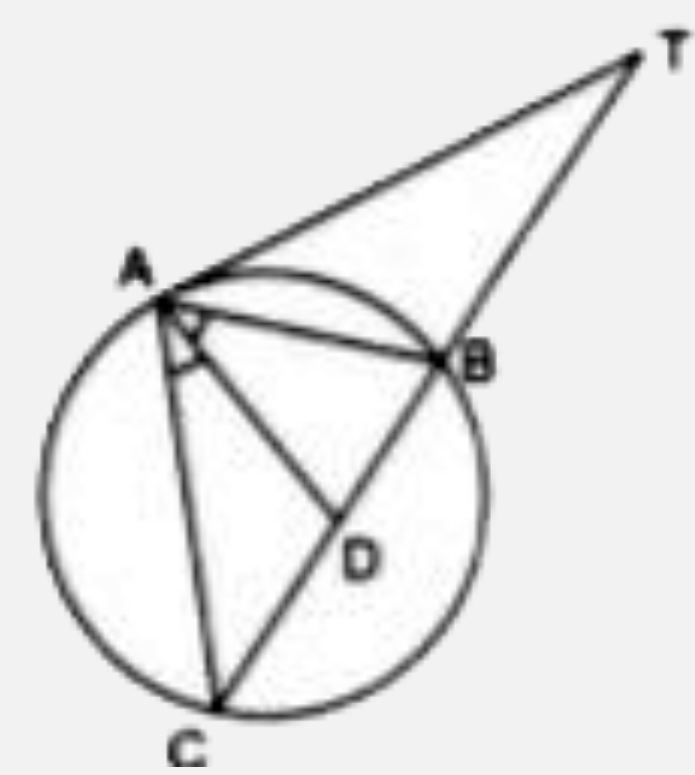
In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
![In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that: /CAD=1/2[/PBA-/PAB]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/SEL_RKB_ICSE_MAT_X_C18_E03_014_Q01.png)
∠CAD=12[∠PBA−∠PAB]
Step by step video & image solution for In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that: /_CAD=1/2[/_PBA-/_PAB] by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that ∠CAD=12(∠PBA−∠PAB)
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
View SolutionIn Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
View SolutionIn a triangle ABC, side AC is greater than side AB and point D lies on side BC such that AD bisects angle BAC. Show that:
∠ADB is acute.
View SolutionIn a triangle ABC, AB = AC. Show that the altitude AD is median also.
View SolutionShow that in an isosceles triangle, angles opposite to equal sides are equal.
View SolutionIf A, B, C are the angles of a triangle ABC and if cosA=sinB2sinC, show that the triangle is isosceles.
View SolutionIn a triangle ABC, if acosA=bcosB, show that the triangle is either isosceles or right angled.
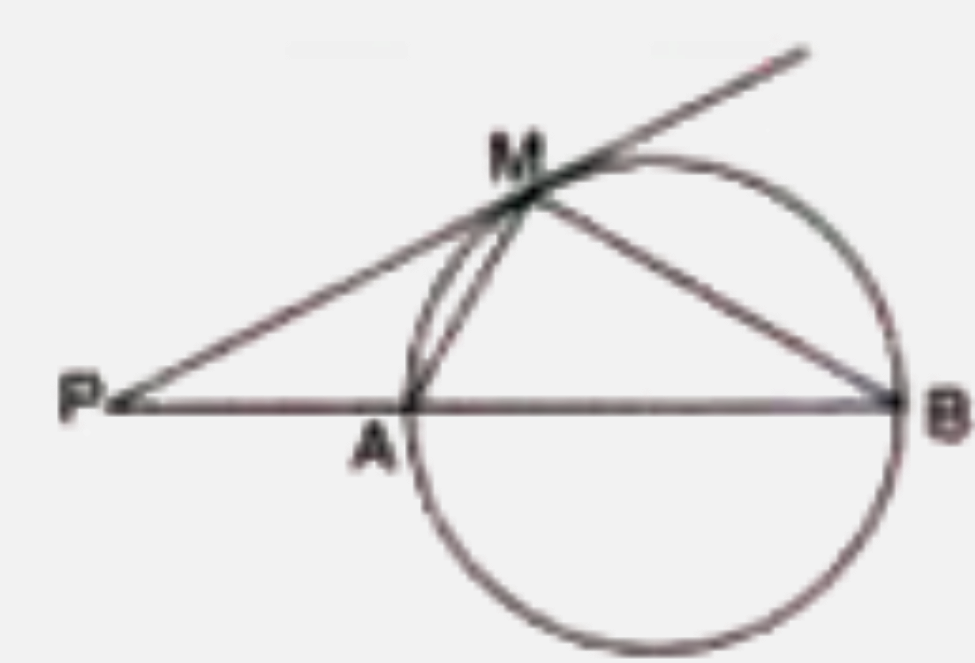
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
View SolutionIn a triangle ABC , if cosA=sinB2sinC , show that the triangle is isosceles.
View Solution
