In Figure , If PQ || BC and PR || CD, prove that $\frac{Q B}{A Q} = \frac{D R}{A R}$ .

Video Solution

|

Answer

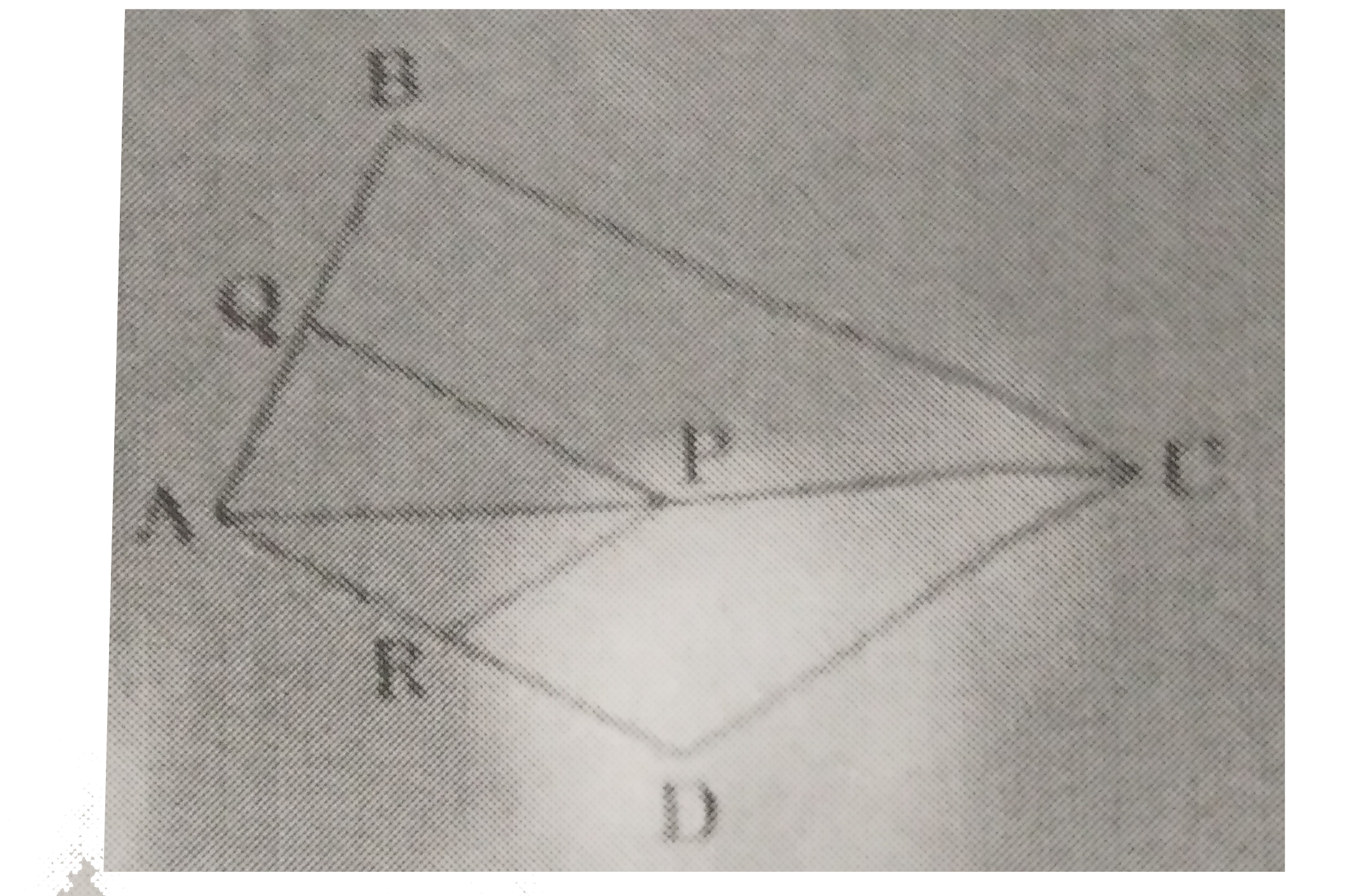
Step by step video & image solution for In Figure , If PQ || BC and PR || CD, prove that (QB)/(AQ)=(DR)/(AR) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Similar Questions

In Figure DE||BC and CD||EF. Prove that $A D^{2} = A B \cdot A F$ .
View Solution
In figure, $C D ∣ ∣ A E$ and $C Y ∣ ∣ B A$ . Prove that $a r (Δ C B X) = a r (Δ A X Y)$ .

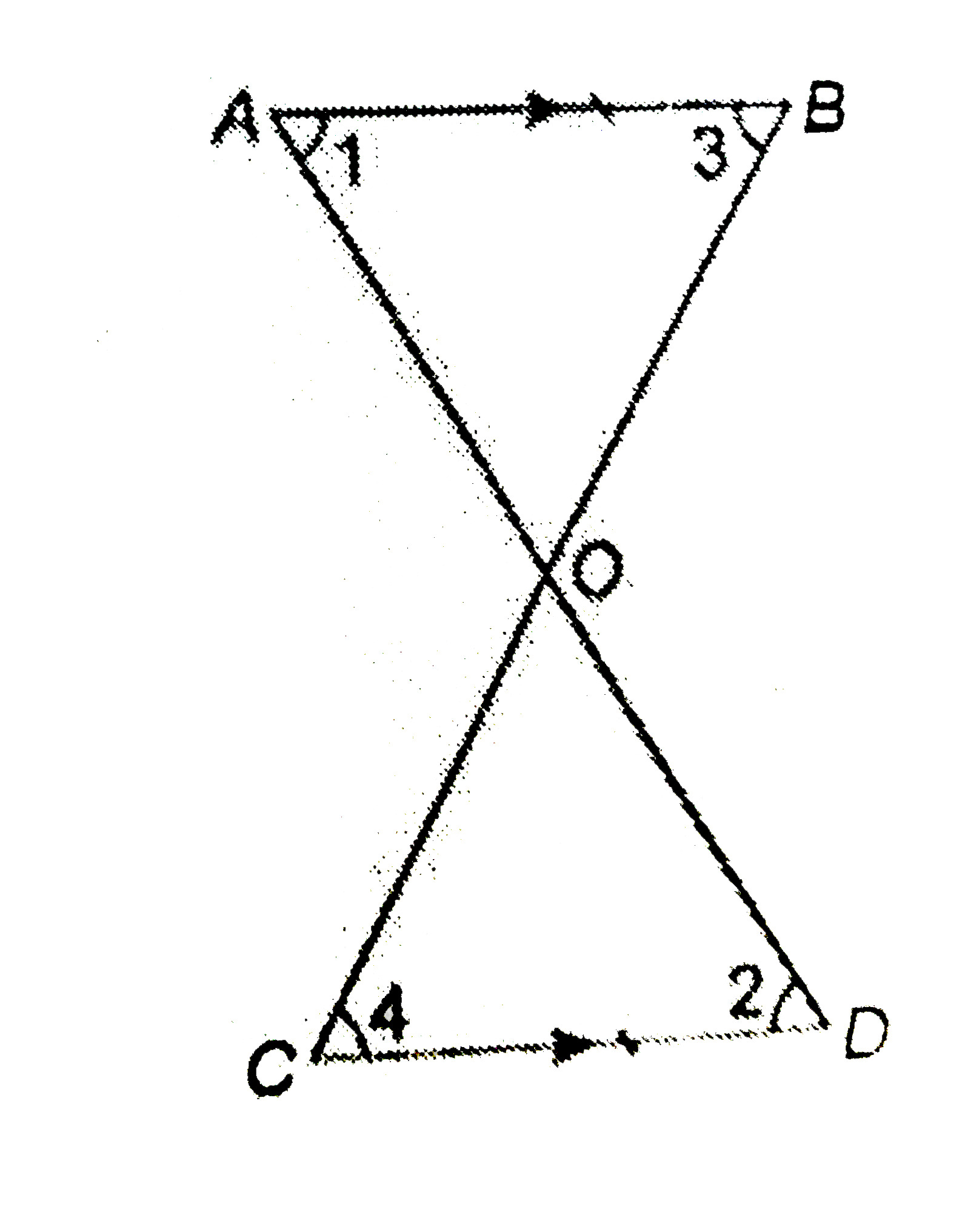
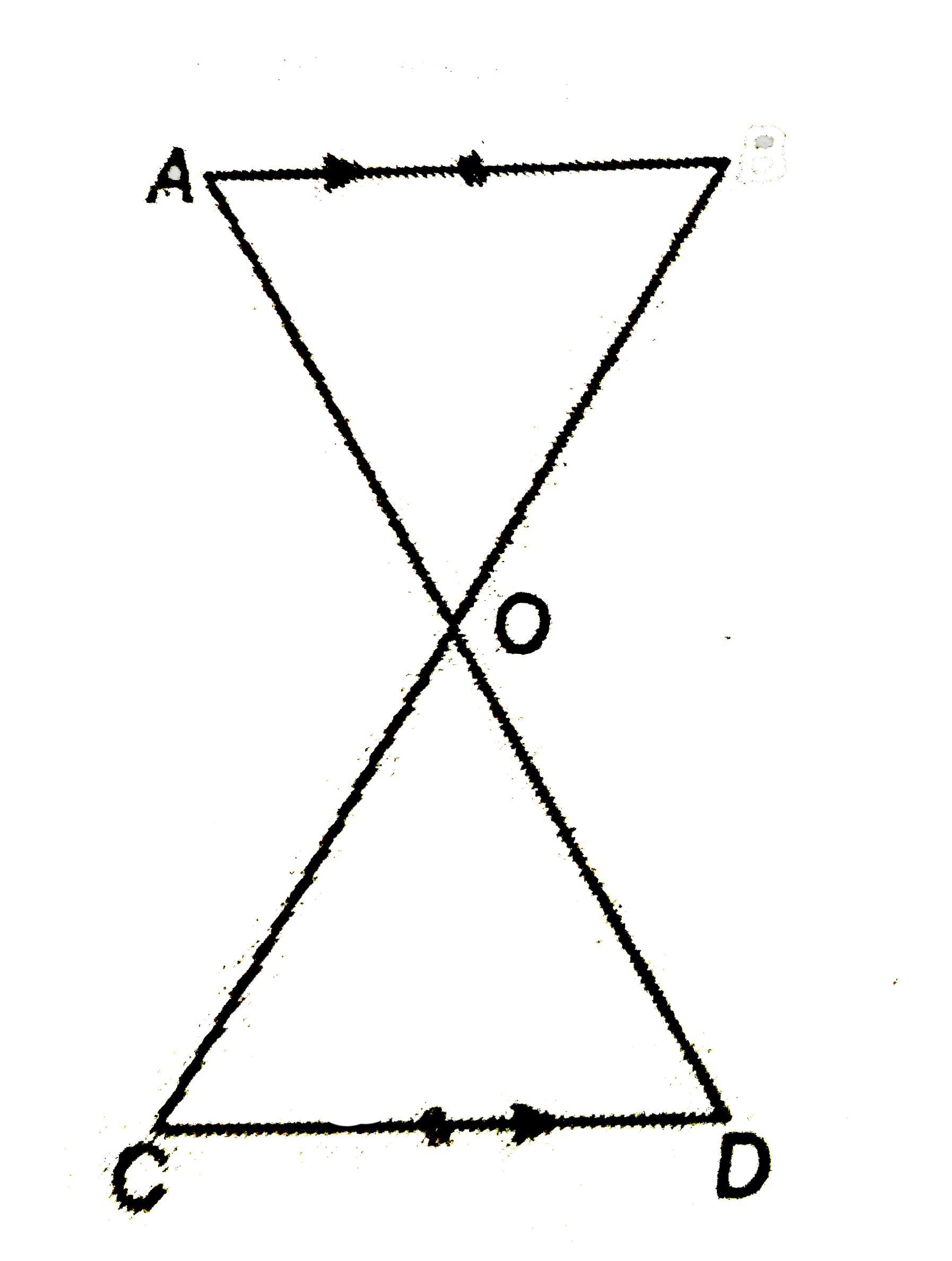
View Solution
In the adjoining figure, AB = CD and AB||CD prove that
(i) $Δ A O B ≅ Δ D O C$
(ii) AD and BC bisect each other at the point O.

View Solution
In the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View Solution
In Figure 3, $A D ⊥ B C$ and $B D = \frac{1}{3} C D$ . Prove that $2 C A^{2} = 2 A B^{2} + B C^{2}$ .
View Solution
In the given figure , $P R > P Q$
Prove that : $A R > A Q$

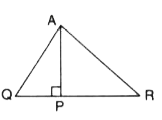
View Solution
In Figure 2, $A D ⊥ B C$ . Prove that $A B^{2} + C D^{2} = B D^{2} + A C^{2}$ .
View Solution
In the given figure AC = BD, prove that AB = CD.

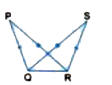
View Solution
In the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) $Δ P Q R ≅ Δ S R Q$
(ii) $∠ P Q R = ∠ S R Q$

View Solution
In the adjoining figure $A B = C D$ and $A B || C D$ prove that :
(i) $Δ A O B ≅ Δ D O G$
(ii) AD and BC bisect each other at point O.

View Solution

In Figure , If PQ || BC and PR || CD, prove that QBAQ=DRAR .

Similar Questions

Recommended Questions

In Figure , If PQ || BC and PR || CD, prove that $\frac{Q B}{A Q} = \frac{D R}{A R}$ .