Let A(p2,−p),B(q2,q),C(r2,−r) be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is 12(p+q)(q+r)(p−r).
To find the maximum area of the parallelogram AFDE inscribed in triangle ABC with vertices A(p², -p), B(q², q), and C(r², -r), we can follow these steps:
Step 1: Determine the coordinates of the vertices
The vertices of triangle ABC are given as:
- A = (p², -p)
- B = (q², q)
- C = (r², -r)
Step 2: Find the equations of the sides of the triangle
We need to find the equations of the lines BC, CA, and AB to determine the positions of points D, E, and F.
1. Line BC:
The slope of line BC can be calculated as:
\text{slope of BC} = \frac{q - (-r)}{q² - r²} = \frac{q + r}{(q - r)(q + r)}
The equation of line BC can be written in point-slope form using point B:
y−q=q+r(q−r)(q+r)(x−q²)
2. Line CA:
The slope of line CA is:
slope of CA=−r−(−p)r²−p²=p−r(r−p)(r+p)
The equation of line CA can be derived similarly.
3. Line AB:
The slope of line AB is:
slope of AB=q−(−p)q²−p²=q+p(q−p)(q+p)
The equation of line AB can be derived similarly.
Step 3: Set up the area of the parallelogram
Let the lengths of segments AF and AE be x and y respectively. The area A of parallelogram AFDE can be expressed as:
A=x⋅y⋅sin(θ)
where θ is the angle between sides AF and AE.
Step 4: Express x and y in terms of p, q, and r
From the equations of the lines, we can express x and y in terms of the coordinates of points A, B, and C.
Step 5: Differentiate the area function
To find the maximum area, we differentiate the area function A with respect to one of the variables (say y) and set the derivative to zero:
dAdy=0
This will help us find critical points.
Step 6: Solve for maximum area
After finding the critical points, we can substitute back to find the maximum area of the parallelogram.
Step 7: Final expression for maximum area
After performing the calculations, we find that the maximum area A of the parallelogram AFDE is given by:
A=12(p+q)(q+r)(p−r)
The vertices of triangle ABC are given as:
- A = (p², -p)
- B = (q², q)
- C = (r², -r)
We need to find the equations of the lines BC, CA, and AB to determine the positions of points D, E, and F.
The slope of line BC can be calculated as:
\text{slope of BC} = \frac{q - (-r)}{q² - r²} = \frac{q + r}{(q - r)(q + r)}
The equation of line BC can be written in point-slope form using point B:
y−q=q+r(q−r)(q+r)(x−q²)
The slope of line CA is:
slope of CA=−r−(−p)r²−p²=p−r(r−p)(r+p)
The equation of line CA can be derived similarly.
The slope of line AB is:
slope of AB=q−(−p)q²−p²=q+p(q−p)(q+p)
The equation of line AB can be derived similarly.
Let the lengths of segments AF and AE be x and y respectively. The area A of parallelogram AFDE can be expressed as:
A=x⋅y⋅sin(θ)
where θ is the angle between sides AF and AE.
From the equations of the lines, we can express x and y in terms of the coordinates of points A, B, and C.
To find the maximum area, we differentiate the area function A with respect to one of the variables (say y) and set the derivative to zero:
dAdy=0
This will help us find critical points.
After finding the critical points, we can substitute back to find the maximum area of the parallelogram.
After performing the calculations, we find that the maximum area A of the parallelogram AFDE is given by:
A=12(p+q)(q+r)(p−r)
Similar Questions
P,Q,R are the points on the sides AB, BC and CA respectively of triangle ABC such that AP:PB=BQ:QC=AR:RC=1:2. Show that PBQR is a parallelogram.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIf P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS , then the value of y is (a) 7 (b) 5 (c) -7 (d) -8
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
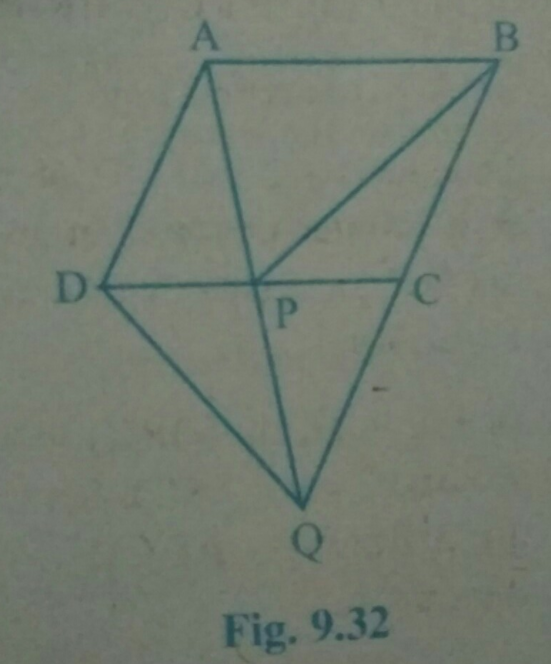
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View Solution
