The angle between diagonal of a cube and diagonal
of a face of the cube will be
cos−1√23
sin−1√23
sin−1(23)
cos−1(1√3)
The correct Answer is:A
To find the angle between the diagonal of a cube and the diagonal of a face of the cube, we can follow these steps:
Step 1: Define the cube and its diagonals
Let's consider a cube with vertices at the following coordinates:
- A(0, 0, 0)
- B(1, 0, 0)
- C(1, 1, 0)
- D(0, 1, 0)
- E(0, 0, 1)
- F(1, 0, 1)
- G(1, 1, 1)
- H(0, 1, 1)
The diagonal of the cube can be represented by the vector from A(0, 0, 0) to G(1, 1, 1). This vector is:
u=(1−0,1−0,1−0)=(1,1,1)
The diagonal of a face (let's take the face ABCD) can be represented by the vector from A(0, 0, 0) to C(1, 1, 0). This vector is:
v=(1−0,1−0,0−0)=(1,1,0)
Step 2: Use the cosine formula to find the angle
To find the angle θ between the two vectors u and v, we can use the formula:
cosθ=u⋅v|u||v|
Step 3: Calculate the dot product u⋅v
The dot product is calculated as follows:
u⋅v=(1)(1)+(1)(1)+(1)(0)=1+1+0=2
Step 4: Calculate the magnitudes of u and v
The magnitude of u is:
|u|=√12+12+12=√3
The magnitude of v is:
|v|=√12+12+02=√2
Step 5: Substitute values into the cosine formula
Now substituting the values into the cosine formula:
cosθ=2√3⋅√2=2√6
Step 6: Rationalize the denominator
To rationalize the denominator:
cosθ=2√6⋅√6√6=2√66=√63
Step 7: Find the angle
To find θ, we take the inverse cosine:
θ=cos−1(√63)
Conclusion
The angle between the diagonal of the cube and the diagonal of a face of the cube is:
θ=cos−1(√63)
Let's consider a cube with vertices at the following coordinates:
- A(0, 0, 0)
- B(1, 0, 0)
- C(1, 1, 0)
- D(0, 1, 0)
- E(0, 0, 1)
- F(1, 0, 1)
- G(1, 1, 1)
- H(0, 1, 1)
u=(1−0,1−0,1−0)=(1,1,1)
v=(1−0,1−0,0−0)=(1,1,0)
To find the angle θ between the two vectors u and v, we can use the formula:
cosθ=u⋅v|u||v|
The dot product is calculated as follows:
u⋅v=(1)(1)+(1)(1)+(1)(0)=1+1+0=2
The magnitude of u is:
|u|=√12+12+12=√3
The magnitude of v is:
|v|=√12+12+02=√2
Now substituting the values into the cosine formula:
cosθ=2√3⋅√2=2√6
To rationalize the denominator:
cosθ=2√6⋅√6√6=2√66=√63
To find θ, we take the inverse cosine:
θ=cos−1(√63)
The angle between the diagonal of the cube and the diagonal of a face of the cube is:
θ=cos−1(√63)
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - B
47 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - C
14 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
Find the angle between any two diagonals of a cube.
View SolutionFind the angel between any two diagonals of a cube.
View SolutionFigure shows a combination of twelve capacitors, each pf capacitance C, forming a cube. Find the equivalent capacitance of the combination (i) between the diagonally opposite corners A and B of the cube (ii) between the diagonally opposite corners A and D of a face of the cube.

View SolutionA ionic compound has a unit cell consisting of a ions at the corners of a cube, B ions on the centres of the faces of the cube but one axis of its faces are missing. The empirical formula for this compound would be -
View SolutionThe square on the diagonal of a cube has an area of 192cm2Calculate :
the side of the cube.
View SolutionThe square on the diagonal of a cube has an area of 192cm2Calculate :
the total surface area of the cube.
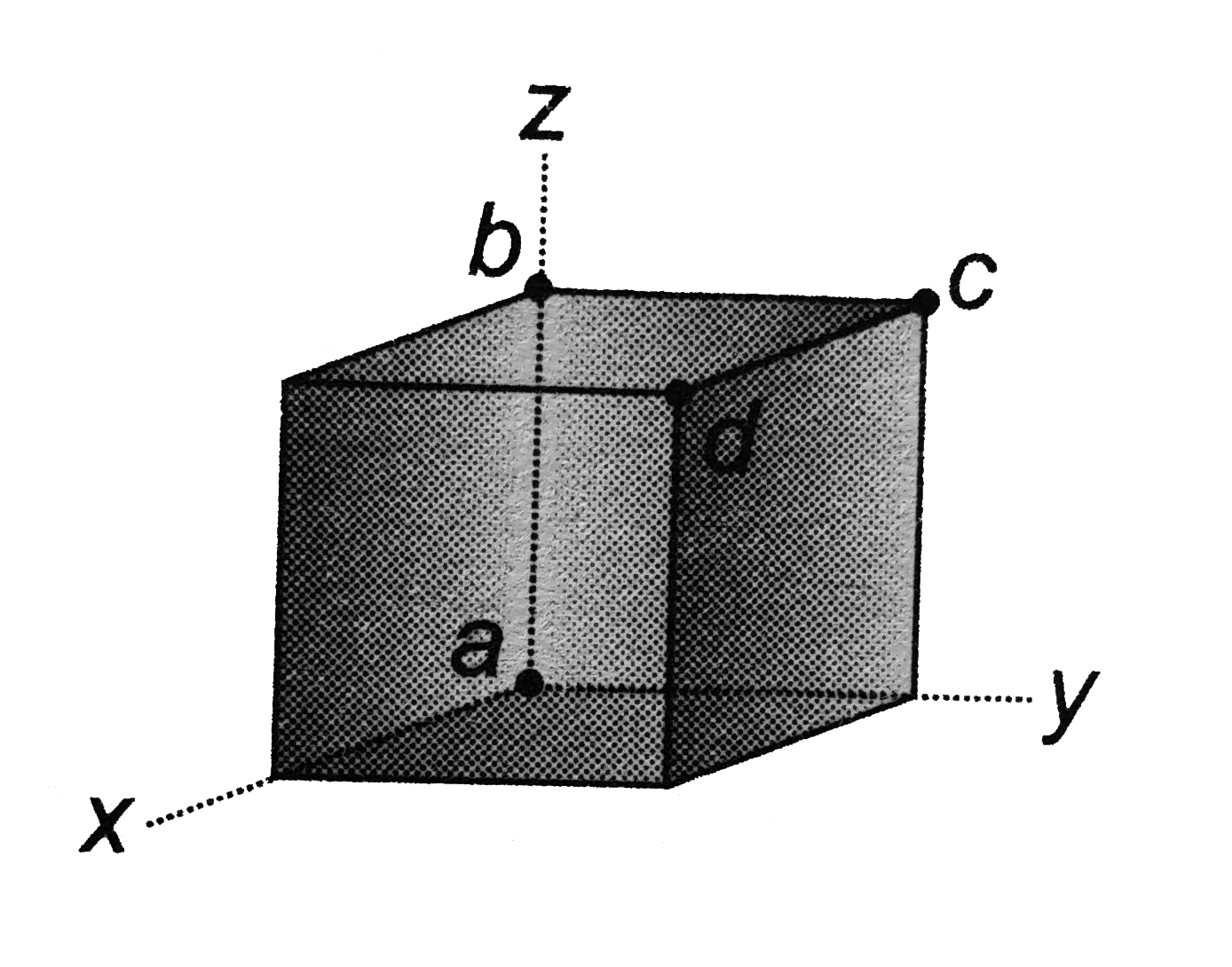
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionThe shortest distance between a diagonal of a unit cube and the edge skew to it, is
View SolutionThe square on the diagonal of a cube has an area of 1875 sq. cm. Calculate:
the side of the cube
View Solution
