Draw the graph of y=sin−1(2x√1−x2)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=sin−1(2x√1−x2)
Clearly, the domain of the function is [-1, 1].
Let x=sinθ,θ∈[−π/2,π/2]
⇒ θ=sin−1x
ocr_image
Now sin(2x√1−x2)=sin−1(2sinθcosθ)
=sin−1(sin2θ)
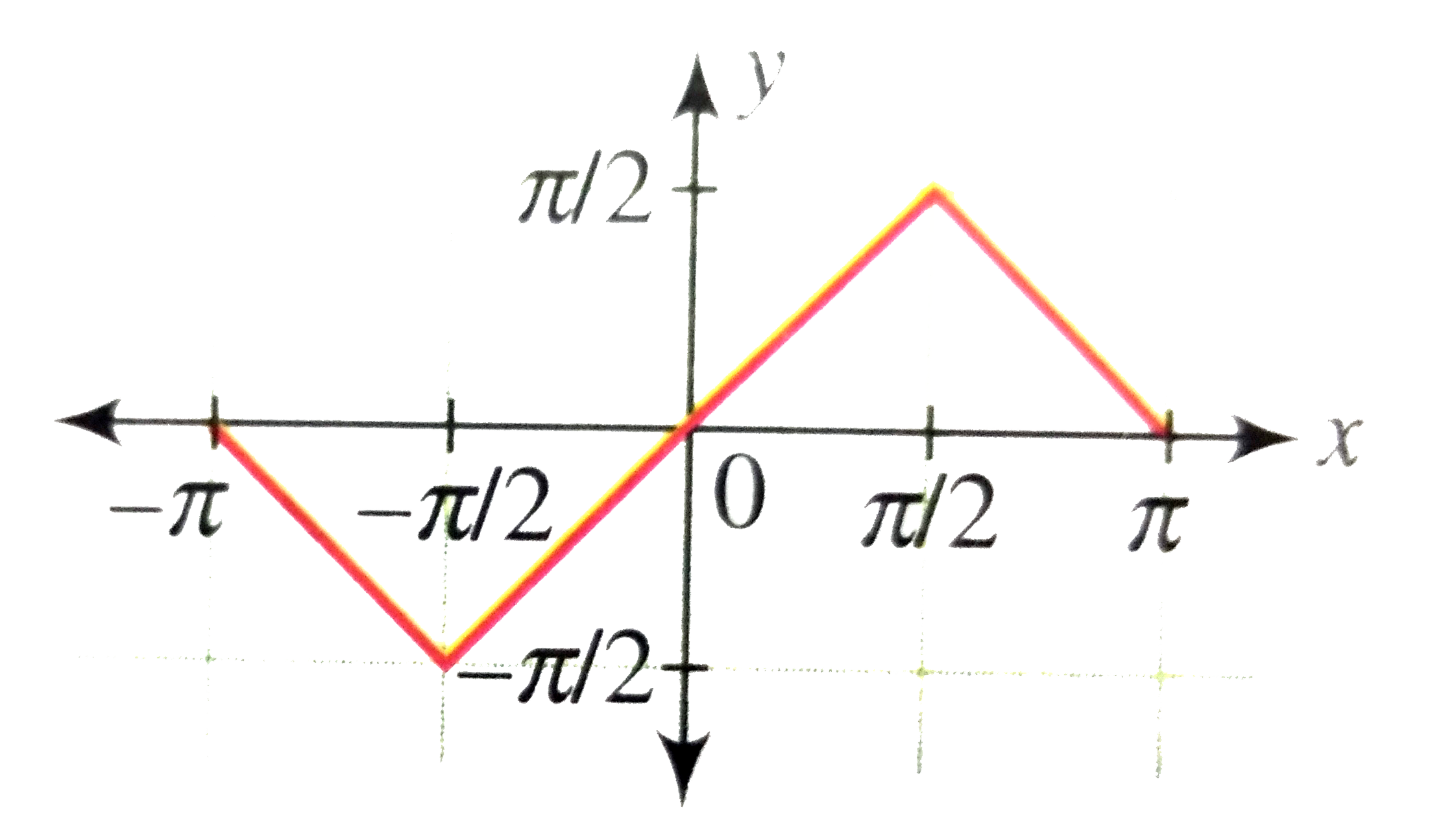
=sin−1(sinα), where α∈[−π,π]
Now consider the graph of y=sin−1(sinα), where α∈[−π,π]
From the grph,
y=f(x)=sin−1(2x√1−x2)=sin−1(sinα)
=⎧⎪⎨⎪⎩−α−π−π≤α<−π/2α−π/2α≤π/2−α+ππ/2<α≤π
=⎧⎪ ⎪⎨⎪ ⎪⎩−2sin−1x−π−π≤2sin−1x<−π/22sin−1x−π/2≤2sin−1x≤π/2−2sin−1x+ππ/2<2sin−1x<π
=⎧⎪ ⎪⎨⎪ ⎪⎩−2sin−1x−π−π≤2sin−1x<−π/42sin−1x−π/π≤4sin−1x≤π/4−2sin−1x+ππ/4<sin−1x<π/2
=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩−2sin−1x−π−1≤x<−1√22sin−1x−1√2≤x≤1√2−2sin−1x+π−1√2≤x≤1
=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩−2√1−x2−1<x<−1√22√1−x2−1<x<−1√2−2√1−x2−1<x<1
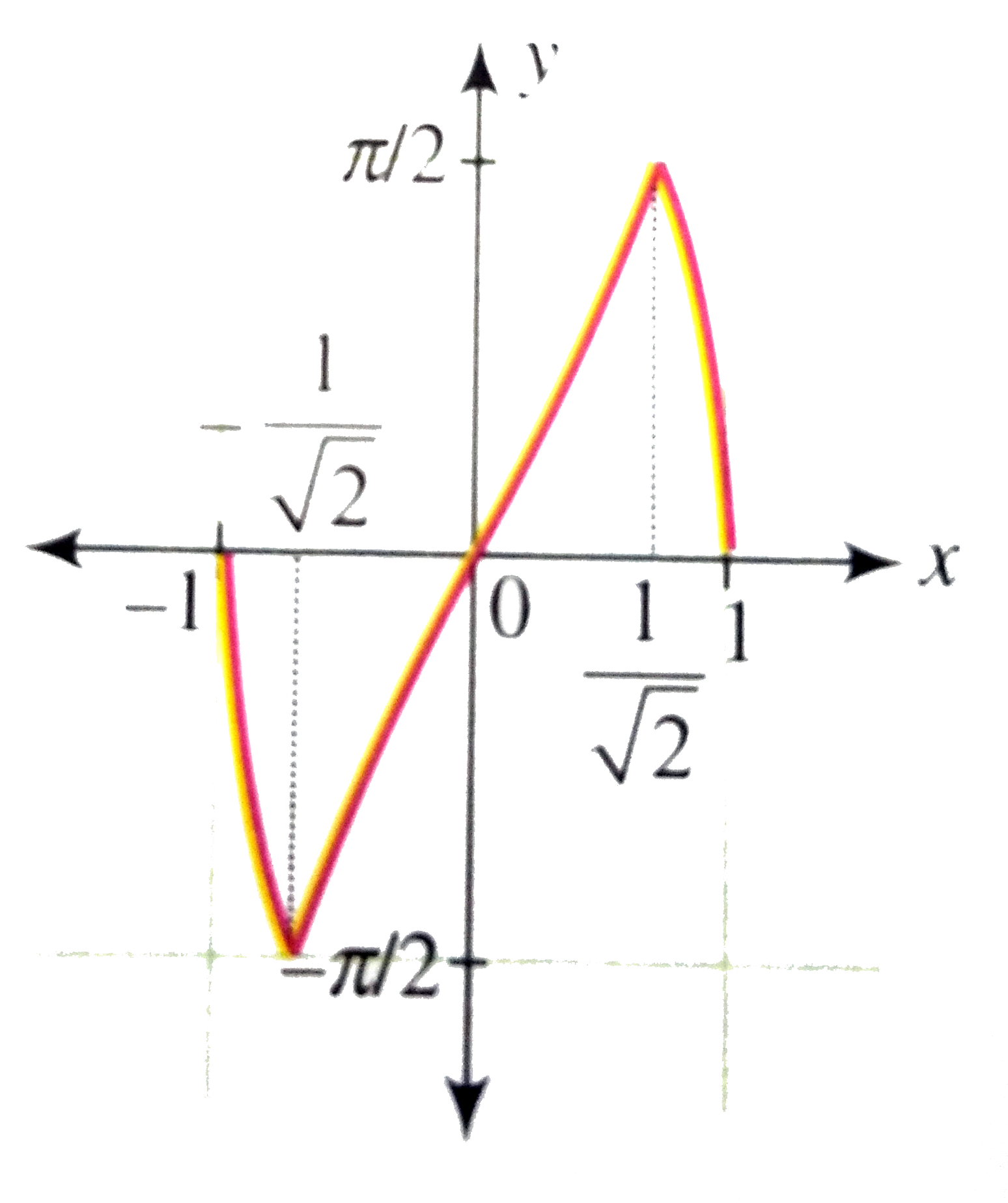
Clearly, y = f(x) is non-differentiable at x=±1√2
y=f(x) inreases for x∈(−1√2,−1√2) and decreases for x∈(−1,−1√2)∪(1√2,1)
For f(x) =−2sin−1x−π
f(−1)=−2sin−1(−1)−π=0,f(−1√2)=−2(−π4)−π=−π2
Thus, sin−1(2x√1−x2) decreases from 0 to −π2 when x increases from -1 to −1√2.
For f(x)=2sin−2x
f(−1√2)=2(−π4)=−π2
f(1√2)=2(π4)=π2
Thus, sin−1(2x√1−x2) increases from =π2toπ2 when x in creases from −1√2to1√2
For f(x)=−2sin−1x+π
f(1√2)=−2(π4)+π=π2,f(1)=−2sin−1(1)+π=0
Thus, sin−1(2x√1−x2) decreases from π2to0
When x increases from 1√2→1.
From this information, we can draw the graph of sin−1(2x√1−x2) as shown in the adjecnt figure.
ocr_image

Updated on:21/07/2023
|