Question

If $O$
is the origin and $OPandOQ$
are the tangents from the origin to the circle $x^2+y^2-6x+4y+8-0$
, then the circumcenter of triangle $OPQ$
is
$(3,-2)$
(b) $(\frac{3}{2},-1)$

$(\frac{3}{4},-\frac{1}{2})$
(d) $(-\frac{3}{2},1)$

Options

A. `(3,-2)`
B. `(3//2,-1)`
C. `(3//4,-1//2)`
D. `(-3//2,1)`

Answer

2

Explanation

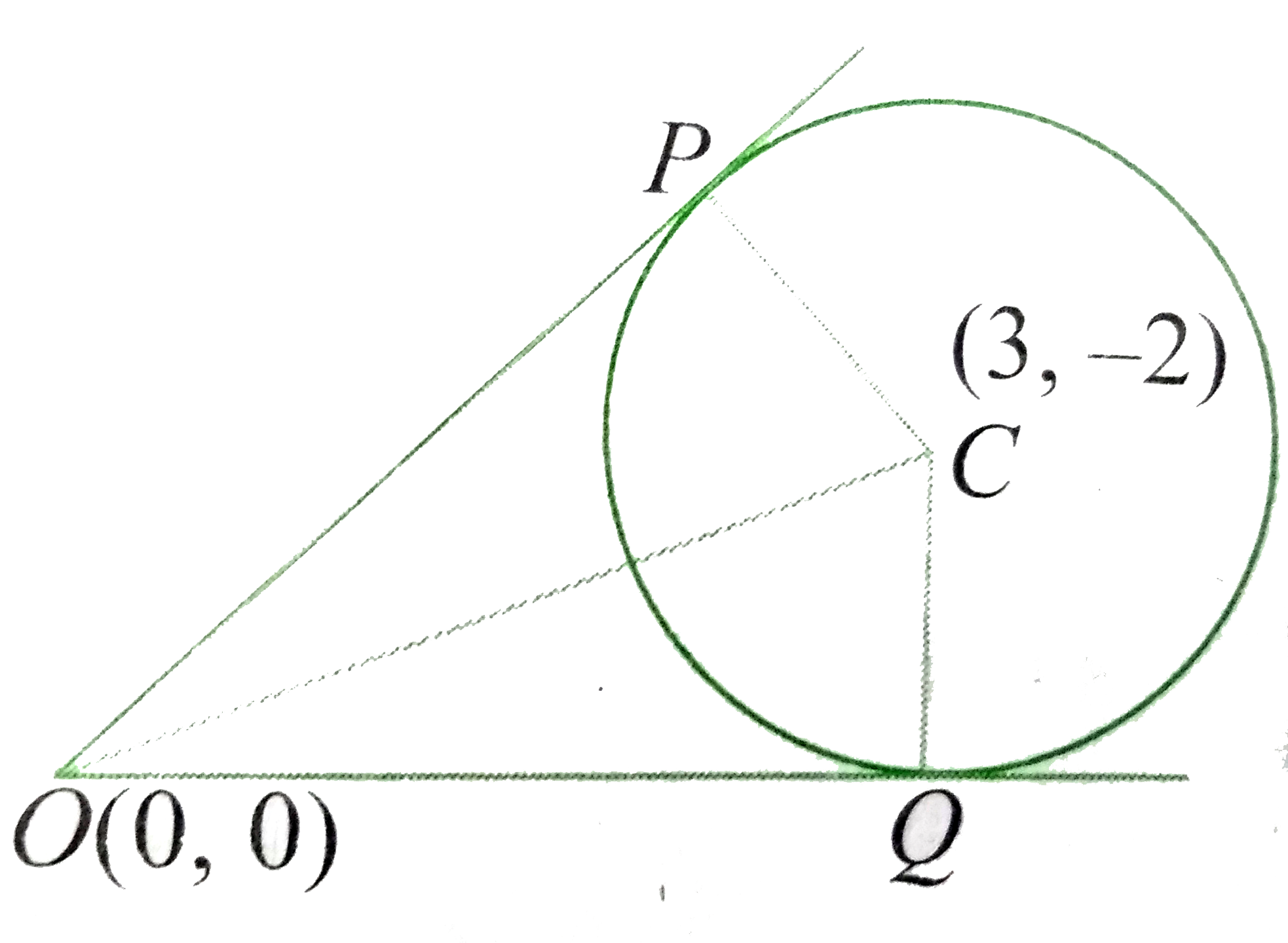
Clearly, OPCQ is a cyclic quadrilateral. Then the circumcircle of `Delta OPQ ` passes through the point C.
For this circle, OC is diameter. Then the center is the midpoint of OC, which is `(3//2,-1)`.