The equation of the line inclined at an angle of $\frac{π}{4}$ to the $X - a ξ s,$ such that the two circles $x^{2} + y^{2} = 4$ and $x^{2} + y^{2} 10 x - 14 y + 65 = 0$ intercept equal length on it, is $2 x - 2 y - 3 = 0$ (b) $2 x - 2 y + 3 = 0$ $x - y + 6 = 0$ (d) $x - y - 6 = 0$

A

$2 x - 2 y - 3 = 0$

B

$2 x - 2 y + 3 = 0$

C

$x - y + 6 = 0$

D

$x - y - 6 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

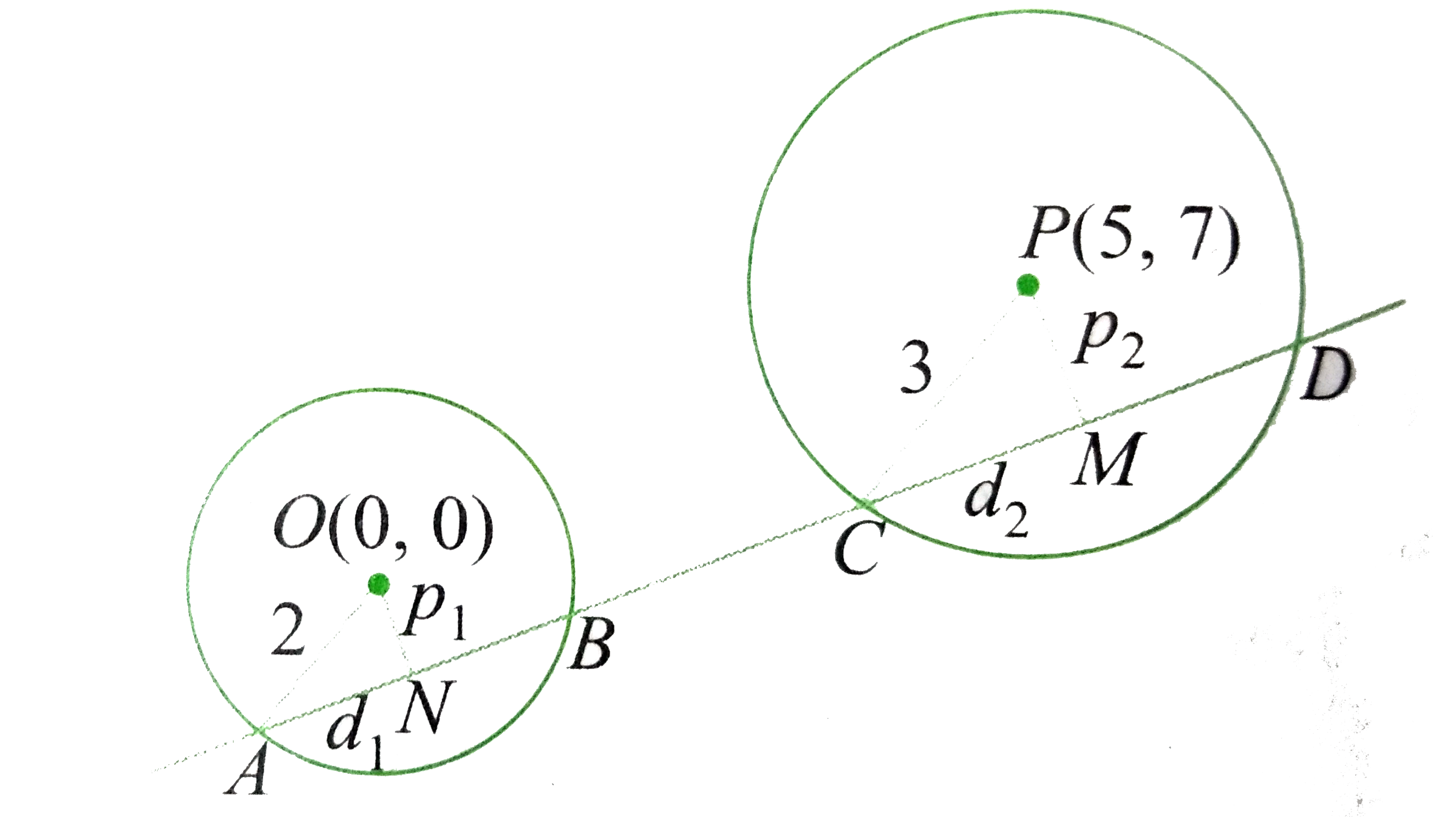
Let the equation of line be
$y = x + c$ or $y - x = c$
Ther perpendicular from (0,0) on line $(1)$ in $∣ ∣ c / \sqrt{2} ∣ ∣$
The perpendicular from $(5, 7)$ on line (1) is $| c - 2 | / \sqrt{2}$
In $Δ A O N$ ,
$\sqrt{2^{2} - {(\frac{c}{\sqrt{2}})}^{2}} = A N$
and in $Δ C P M$
$\sqrt{3^{2} - {(\frac{2 - c}{\sqrt{2}})}^{2}} = C M$
Given $A N = C M$
or $4 - \frac{c^{2}}{2} = 9 = 9 - \frac{{(2 - c)}^{2}}{2}$ or $c = - \frac{3}{2}$
Therefore, the equation of the line is
$y = x - \frac{3}{2}$ or $2 x - 2 y - 3 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile