Find the points of inflection for f(x)=sinx f(x)=3x4−4x3 f(x)=x13
f(x)=cosx
⇒ f(x)(=cosx)
⇒ f(x)=-sinx
f(x)=0
⇒x=nπ,n∈Z
So points of inflection are x= nπ,n∈z
All all points of inflection tangent crosses the curved

(ii) f(x)=3x4−4x3
∴f(x)=12x3−12x2
⇒f(x)=36x2−24x
Now f(x)=0
⇒x=0,2/3which are points of inflection

We observe that tangents to the curve at x =0 and x =23 are crossing the curve.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Solved Examples20videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Find the points of inflection for (a)f(x)=sinx (b)f(x)=3x4−4x3
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1. Also, find the corresponding local maximum and local minimum values.
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind f ' (x) if f(x)=2x3−5x2−4x+3 ,
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
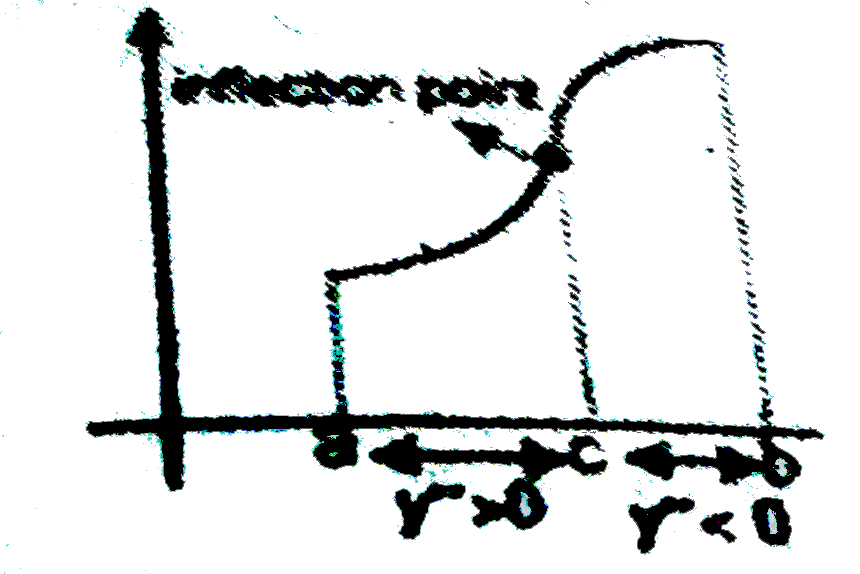
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionIf f(x)=3x4−5x2+9, find f(x−1) .
View SolutionFind the domain and range function f(x)=x2−3x+2x2−4x+3.
View SolutionFind the critical points of the function f(x) =4x3−6x2−24x+9iff(i)x∈[0,3](ii)x∈[−3,3](iii)x∈[−1,2]
View Solution

