Find the points of inflection for (a)f(x)=sinx (b)f(x)=3x4−4x3
To find the points of inflection for the given functions, we need to follow these steps:
(a) For f(x)=sinx
1. Find the first derivative f′(x):
f′(x)=cosx
2. Find the second derivative f′′(x):
f′′(x)=−sinx
3. Set the second derivative equal to zero:
−sinx=0⟹sinx=0
4. Solve for x:
The sine function is equal to zero at integer multiples of π:
x=nπ(n∈Z)
Points of Inflection for f(x)=sinx:
The points of inflection occur at x=nπ, where n is any integer.
---
(b) For f(x)=3x4−4x3
1. Find the first derivative f′(x):
f′(x)=12x3−12x2
2. Find the second derivative f′′(x):
f′′(x)=36x2−24x
3. Factor the second derivative:
f′′(x)=12x(3x−2)
4. Set the second derivative equal to zero:
12x(3x−2)=0
5. Solve for x:
- From 12x=0:
x=0
- From 3x−2=0:
3x=2⟹x=23
Points of Inflection for f(x)=3x4−4x3:
The points of inflection occur at x=0 and x=23.
---
Summary of Points of Inflection:
- For f(x)=sinx: x=nπ (where n is an integer)
- For f(x)=3x4−4x3: x=0 and x=23
---
f′(x)=cosx
f′′(x)=−sinx
−sinx=0⟹sinx=0
The sine function is equal to zero at integer multiples of π:
x=nπ(n∈Z)
The points of inflection occur at x=nπ, where n is any integer.
f′(x)=12x3−12x2
f′′(x)=36x2−24x
f′′(x)=12x(3x−2)
12x(3x−2)=0
- From 12x=0:
x=0
- From 3x−2=0:
3x=2⟹x=23
The points of inflection occur at x=0 and x=23.
- For f(x)=sinx: x=nπ (where n is an integer)
- For f(x)=3x4−4x3: x=0 and x=23
Similar Questions
Find the points of inflection for f(x)=sinx f(x)=3x4−4x3 f(x)=x13
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1. Also, find the corresponding local maximum and local minimum values.
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind f '(x) If f(x)=sinxx
View SolutionWhich of the following function/functions has/have point of inflection? f(x)=x67 (b) f(x)=x6 f(x)=cosx+2x (d) f(x)=x|x|
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
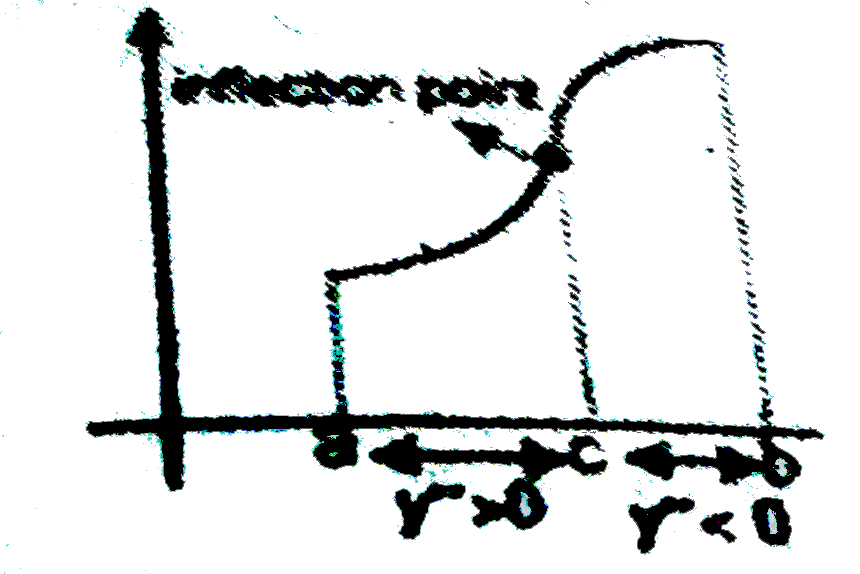
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionLet f(x)be real valued continous funcion on R defined as f(x) =x2e−|x|
Number of points of inflection for y=f(x) is (a) 1 (b) 2 (c) 3 (d) 4
View SolutionFind the domain of the following following functions:
(a) f(x)=sin−1x
(b) f(x)=sin−1(|x−1|−2)
(c ) f(x)=cos−1(1+3x+2x2)
(d ) f(x)=sin−1(x−3)√9−x2
(e ) f(x)=cos−1(6−3x4)+cosec−1(x−12)
(f) f(x)= ⎷sec−1(2−|x|4)
View Solution
