Calculate the mean deviation about median age for the age distribution of 100 persons given below: Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55 Number 5 6 12 14 26 12 16 9
To calculate the mean deviation about the median age for the given age distribution of 100 persons, we will follow these steps:
Step 1: Create a frequency distribution table
We will first summarize the age distribution in a table format with the midpoints of each age group.
| Age Group | Frequency (f) | Midpoint (x) | Cumulative Frequency (cf) |
|-----------|---------------|--------------|---------------------------|
| 16-20 | 5 | 18 | 5 |
| 21-25 | 6 | 23 | 11 |
| 26-30 | 12 | 28 | 23 |
| 31-35 | 14 | 33 | 37 |
| 36-40 | 26 | 38 | 63 |
| 41-45 | 12 | 43 | 75 |
| 46-50 | 16 | 48 | 91 |
| 51-55 | 9 | 53 | 100 |
Step 2: Calculate the median
The total number of persons (N) is 100. To find the median, we need to find the cumulative frequency that exceeds N/2 = 50.
From the cumulative frequency column, we see that the median class is 36-40 (since the cumulative frequency just exceeds 50 at 63).
Now we can use the formula for the median:
Median=L+⎛⎝N2−cff⎞⎠×h
Where:
- L = lower boundary of the median class = 35.5
- N = total frequency = 100
- cf = cumulative frequency of the class before the median class = 37
- f = frequency of the median class = 26
- h = width of the median class = 5
Substituting the values:
Median=35.5+(50−3726)×5
=35.5+(1326)×5
=35.5+2.5=38
Step 3: Calculate the mean deviation
Next, we will calculate the mean deviation about the median. We will create a new column for |x−Median| and multiply it by the frequency f.
| Age Group | Frequency (f) | Midpoint (x) | |x - Median| | f * |x - Median| |
|-----------|---------------|--------------|----------------|-----------------------|
| 16-20 | 5 | 18 | 20 | 100 |
| 21-25 | 6 | 23 | 15 | 90 |
| 26-30 | 12 | 28 | 10 | 120 |
| 31-35 | 14 | 33 | 5 | 70 |
| 36-40 | 26 | 38 | 0 | 0 |
| 41-45 | 12 | 43 | 5 | 60 |
| 46-50 | 16 | 48 | 10 | 160 |
| 51-55 | 9 | 53 | 15 | 135 |
Now we sum the last column:
∑f∗|x−Median|=100+90+120+70+0+60+160+135=775
Step 4: Calculate the mean deviation
The mean deviation (MD) is given by:
MD=∑f∗|x−Median|N
Substituting the values:
MD=775100=7.75
Final Result
The mean deviation about the median age is 7.75.
---
|-----------|---------------|--------------|---------------------------|
| 16-20 | 5 | 18 | 5 |
| 21-25 | 6 | 23 | 11 |
| 26-30 | 12 | 28 | 23 |
| 31-35 | 14 | 33 | 37 |
| 36-40 | 26 | 38 | 63 |
| 41-45 | 12 | 43 | 75 |
| 46-50 | 16 | 48 | 91 |
| 51-55 | 9 | 53 | 100 |
- L = lower boundary of the median class = 35.5
- N = total frequency = 100
- cf = cumulative frequency of the class before the median class = 37
- f = frequency of the median class = 26
- h = width of the median class = 5
=35.5+(1326)×5
=35.5+2.5=38
|-----------|---------------|--------------|----------------|-----------------------|
| 16-20 | 5 | 18 | 20 | 100 |
| 21-25 | 6 | 23 | 15 | 90 |
| 26-30 | 12 | 28 | 10 | 120 |
| 31-35 | 14 | 33 | 5 | 70 |
| 36-40 | 26 | 38 | 0 | 0 |
| 41-45 | 12 | 43 | 5 | 60 |
| 46-50 | 16 | 48 | 10 | 160 |
| 51-55 | 9 | 53 | 15 | 135 |
Topper's Solved these Questions
Similar Questions
Calculate the mean deviatioin about median age for the age distribution of 100 persons given below:
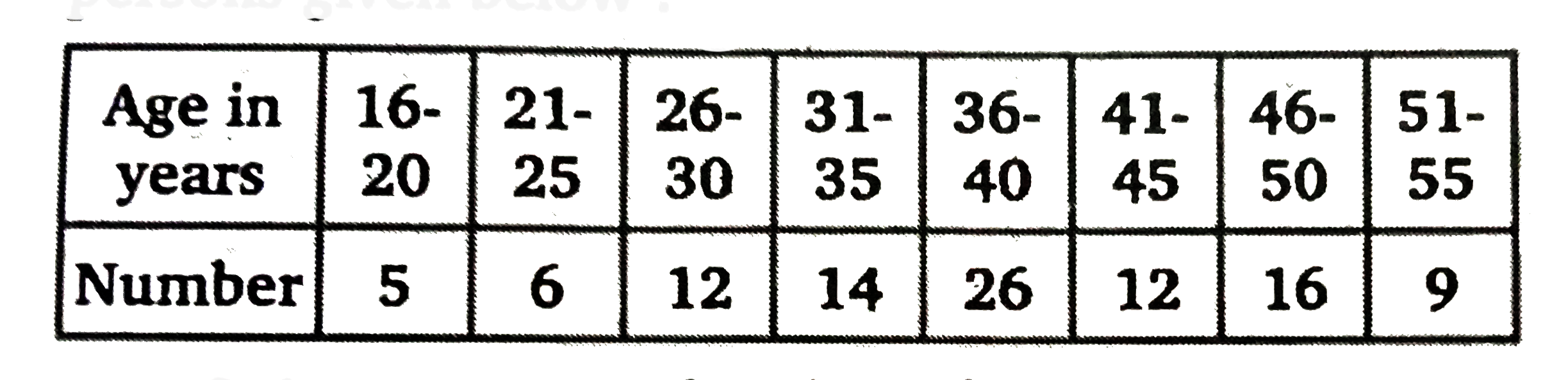
View SolutionCalculate the mean deviation about the median of the following frequency distribution: 5 7 9 11 13 15 17 Having Frequency 2 4 6 8 10 12 8
View SolutionCalculate mean deviation from the median for the following distribution: xi: 10 15 20 25 30 35 40 45 fi: 7 3 8 5 6 8 4 9
View SolutionCalculate the mean deviation about the mean for the following frequency distribution Class interval 0−4,4−8,8−12,12−16,16−20 Frequency 4,6,8,5,2
View SolutionFind the Mean deviation (about Mean) of the following observation 2,3,5,6,9,10,12,17,20,26.
View SolutionCalculate the mean and standard deviation for the following table given the age distribution of a group of people: Age: 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of persons: 3 51 122 141 130 51 2
View SolutionCalculate the mean and standard deviation for the following table given the age distribution of a group of people: Age: 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of persons: 3 51 122 141 130 51 2
View SolutionCalculate mean deviation from the median for the following distribution: xi: , 10, 15, 20, 25, 30, 35, 40, 45 fi: , 7, 3, 8, 5, 6, 8, 4, 9
View SolutionFind the mean deviation about the median of the following frequency distribution: Class:, 0-6, 6-12, 12-18, 18-24, 24-30 Frequency:, 8, 10, 12, 9, 5
View SolutionFind the mean deviation about the median of the following frequency distribution: Class:, 0-6, 6-12, 12-18, 18-24, 24-30 Frequency:, 8, 10, 12, 9, 5
View Solution
