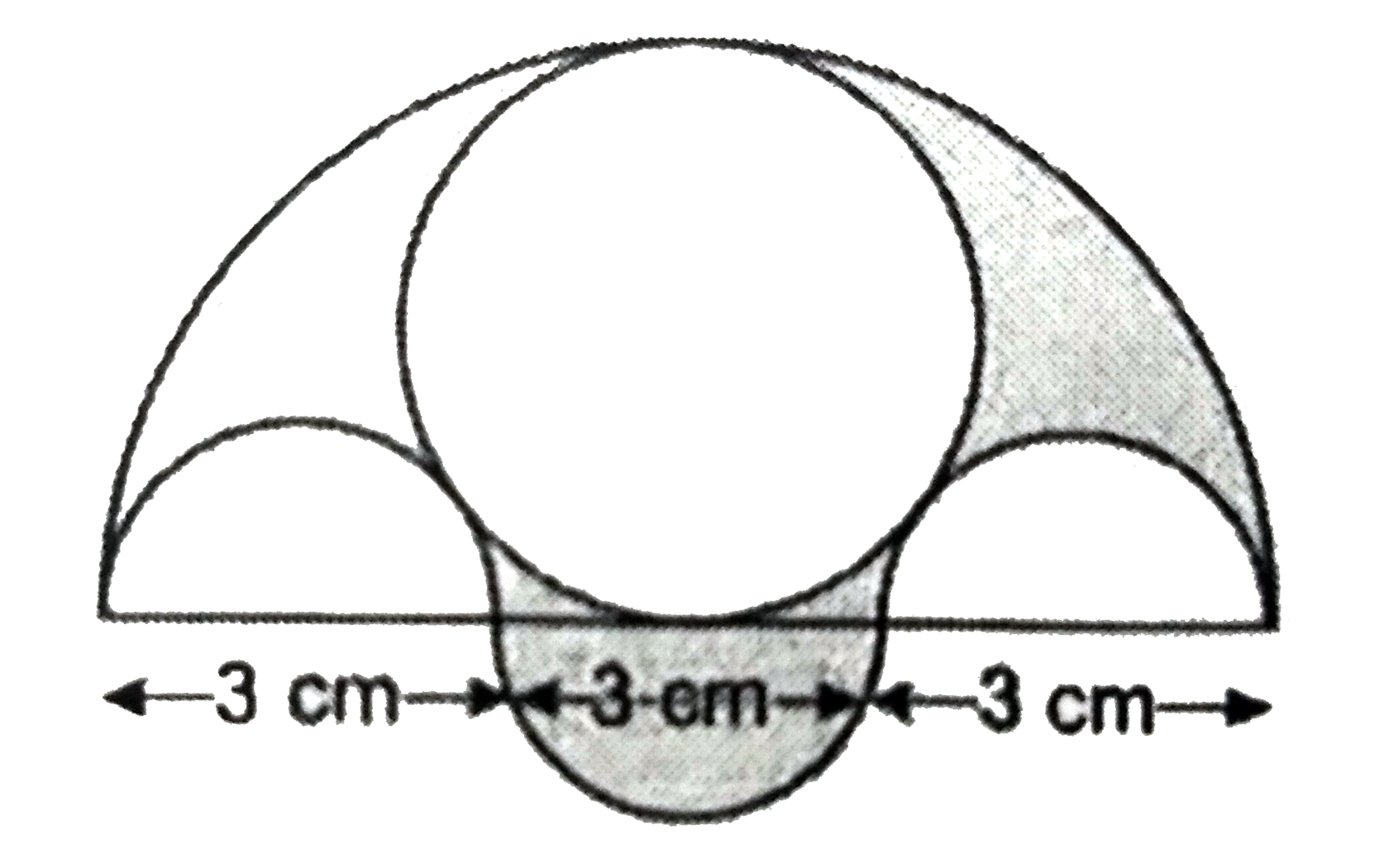
In Figure, there are three semicircles, A, B and C having diameter 3cm each, and another semicircle E having a circle D with diameter 4.5cm are shown. Calculate: (i)the area of the shaded region. (ii)the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.
To solve the problem step by step, we need to calculate the area of the shaded region formed by the semicircles and then find the cost of painting that area.
Step 1: Identify the diameters and radii of the semicircles
- The diameters of semicircles A, B, and C are each 3 cm.
- The diameter of semicircle E (which is the larger semicircle) is 9 cm (since it combines three semicircles of diameter 3 cm).
- The diameter of circle D is 4.5 cm.
Step 2: Calculate the radii
- Radius of semicircles A, B, and C:
rsmall=32=1.5 cm
- Radius of semicircle E:
rlarge=92=4.5 cm
- Radius of circle D:
rcircle=4.52=2.25 cm
Step 3: Calculate the area of the larger semicircle (E)
The area of a semicircle is given by the formula:
Area=12πr2
Thus, the area of semicircle E is:
AreaE=12π(4.5)2=12π(20.25)=10.125π cm2
Step 4: Calculate the area of circle D
The area of a circle is given by the formula:
Area=πr2
Thus, the area of circle D is:
AreaD=π(2.25)2=π(5.0625)=5.0625π cm2
Step 5: Calculate the area of the small semicircles (A, B, C)
Since there are two small semicircles (A and C) and one small semicircle (B), we calculate the area of one small semicircle:
Areasmall=12π(1.5)2=12π(2.25)=1.125π cm2
The total area of the three small semicircles is:
Areasmall total=3×1.125π=3.375π cm2
Step 6: Calculate the area of the shaded region
The area of the shaded region is given by:
Areashaded=AreaE−AreaD−Areasmall total
Substituting the values:
Areashaded=10.125π−5.0625π−3.375π=(10.125−5.0625−3.375)π=1.6875π cm2
Step 7: Calculate the numerical value of the shaded area
Using π≈3.14:
Areashaded≈1.6875×3.14≈5.2905 cm2
Step 8: Calculate the cost of painting the shaded region
The cost of painting is given as 25 paise per cm². Therefore, the total cost is:
Cost=25×Areashaded=25×5.2905≈132.2625 paise
Converting paise to rupees (100 paise = 1 rupee):
Cost in rupees=132.2625100≈1.322625 rupees
Rounding to the nearest rupee gives us:
Cost≈1 rupee
Final Answers:
(i) The area of the shaded region is approximately 5.29 cm2.
(ii) The cost of painting the shaded region is approximately 1 rupee.
- The diameters of semicircles A, B, and C are each 3 cm.
- The diameter of semicircle E (which is the larger semicircle) is 9 cm (since it combines three semicircles of diameter 3 cm).
- The diameter of circle D is 4.5 cm.
- Radius of semicircles A, B, and C:
rsmall=32=1.5 cm
- Radius of semicircle E:
rlarge=92=4.5 cm
- Radius of circle D:
rcircle=4.52=2.25 cm
The area of a semicircle is given by the formula:
Area=12πr2
Thus, the area of semicircle E is:
AreaE=12π(4.5)2=12π(20.25)=10.125π cm2
The area of a circle is given by the formula:
Area=πr2
Thus, the area of circle D is:
AreaD=π(2.25)2=π(5.0625)=5.0625π cm2
Since there are two small semicircles (A and C) and one small semicircle (B), we calculate the area of one small semicircle:
Areasmall=12π(1.5)2=12π(2.25)=1.125π cm2
The total area of the three small semicircles is:
Areasmall total=3×1.125π=3.375π cm2
The area of the shaded region is given by:
Areashaded=AreaE−AreaD−Areasmall total
Substituting the values:
Areashaded=10.125π−5.0625π−3.375π=(10.125−5.0625−3.375)π=1.6875π cm2
Using π≈3.14:
Areashaded≈1.6875×3.14≈5.2905 cm2
The cost of painting is given as 25 paise per cm². Therefore, the total cost is:
Cost=25×Areashaded=25×5.2905≈132.2625 paise
Converting paise to rupees (100 paise = 1 rupee):
Cost in rupees=132.2625100≈1.322625 rupees
Rounding to the nearest rupee gives us:
Cost≈1 rupee
(i) The area of the shaded region is approximately 5.29 cm2.
(ii) The cost of painting the shaded region is approximately 1 rupee.
Topper's Solved these Questions
Similar Questions
In Figure, there are three semicircles, A, B and C having diameter 3cm each, and another semicircle E having a circle D with diameter 4.5cm are shown. Calculate: (i)the area of the shaded region. (ii)the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.
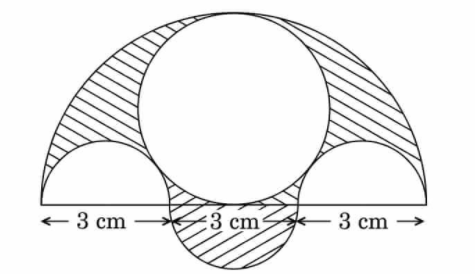
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.

View SolutionIn Fig. , ABCD is a rectangle, having AB=20 cm and BC=14 cm . Two sectors of 180o have been cut off. Calculate: (i) the area of the shaded region. (ii) the length of the boundary of the shaded region.
View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region

View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
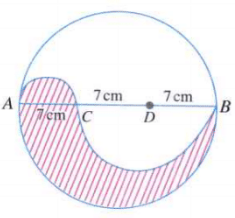
View SolutionGiven is a circle with AB as a diameter of 21 cm. Points C and D lie on the diameter such that AC=7cm,CD=DB=7cm. Semicircles are drawn on the diameter as shown. Find the area of the shaded region.
View Solution
