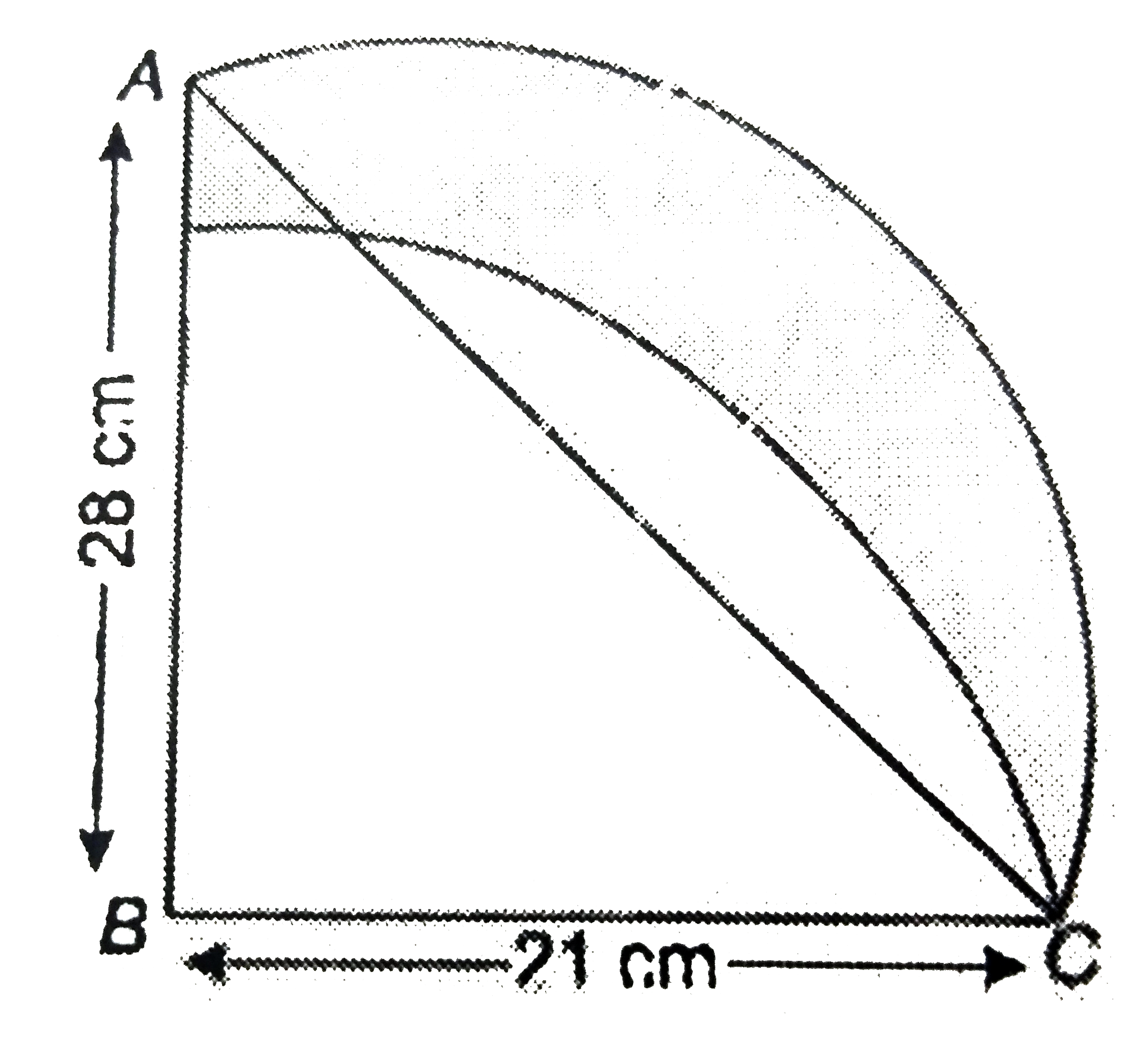
In Figure, ABC is a right-angled triangle, ∠B=900,AB=28 cm and BC=21 cm With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
To find the area of the shaded region in the given problem, we will follow these steps:
Step 1: Calculate the area of triangle ABC
Triangle ABC is a right-angled triangle with:
- AB (height) = 28 cm
- BC (base) = 21 cm
The area of a triangle is given by the formula:
Area of triangle=12×base×height
Substituting the values:
Area of triangle ABC=12×21×28=12×588=294 cm2
Step 2: Calculate the length of AC (diameter of the semicircle)
Using the Pythagorean theorem:
AC2=AB2+BC2
Substituting the values:
AC2=282+212=784+441=1225
Taking the square root:
AC=√1225=35 cm
Step 3: Calculate the radius of the semicircle
The radius r1 of the semicircle is half of the diameter AC:
r1=AC2=352=17.5 cm
Step 4: Calculate the area of the semicircle
The area of a semicircle is given by:
Area of semicircle=12πr21
Substituting the value of r1:
Area of semicircle=12π(17.5)2=12π×306.25=306.25π2≈480.57 cm2(using π≈3.14)
Step 5: Calculate the radius of the quarter circle
The radius r2 of the quarter circle is equal to BC:
r2=21 cm
Step 6: Calculate the area of the quarter circle
The area of a quarter circle is given by:
Area of quarter circle=14πr22
Substituting the value of r2:
Area of quarter circle=14π(21)2=14π×441=441π4≈346.36 cm2(using π≈3.14)
Step 7: Calculate the area of the shaded region
The area of the shaded region is given by:
Area of shaded region=Area of triangle ABC+Area of semicircle−Area of quarter circle
Substituting the calculated areas:
Area of shaded region=294+480.57−346.36≈428.21 cm2
Final Answer
The area of the shaded region is approximately:
Area of shaded region≈428.21 cm2
Triangle ABC is a right-angled triangle with:
- AB (height) = 28 cm
- BC (base) = 21 cm
Area of triangle=12×base×height
Substituting the values:
Area of triangle ABC=12×21×28=12×588=294 cm2
Using the Pythagorean theorem:
AC2=AB2+BC2
Substituting the values:
AC2=282+212=784+441=1225
Taking the square root:
AC=√1225=35 cm
The radius r1 of the semicircle is half of the diameter AC:
r1=AC2=352=17.5 cm
The area of a semicircle is given by:
Area of semicircle=12πr21
Substituting the value of r1:
Area of semicircle=12π(17.5)2=12π×306.25=306.25π2≈480.57 cm2(using π≈3.14)
The radius r2 of the quarter circle is equal to BC:
r2=21 cm
The area of a quarter circle is given by:
Area of quarter circle=14πr22
Substituting the value of r2:
Area of quarter circle=14π(21)2=14π×441=441π4≈346.36 cm2(using π≈3.14)
The area of the shaded region is given by:
Area of shaded region=Area of triangle ABC+Area of semicircle−Area of quarter circle
Substituting the calculated areas:
Area of shaded region=294+480.57−346.36≈428.21 cm2
The area of the shaded region is approximately:
Area of shaded region≈428.21 cm2
Topper's Solved these Questions
Similar Questions
In Figure, ABC is a right-angled triangle, ∠B=900,AB=28 cm and BC=21 cm With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
View SolutionIn the figure, in ΔABC,∠B=90∘,AB=28cmandBC=21cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
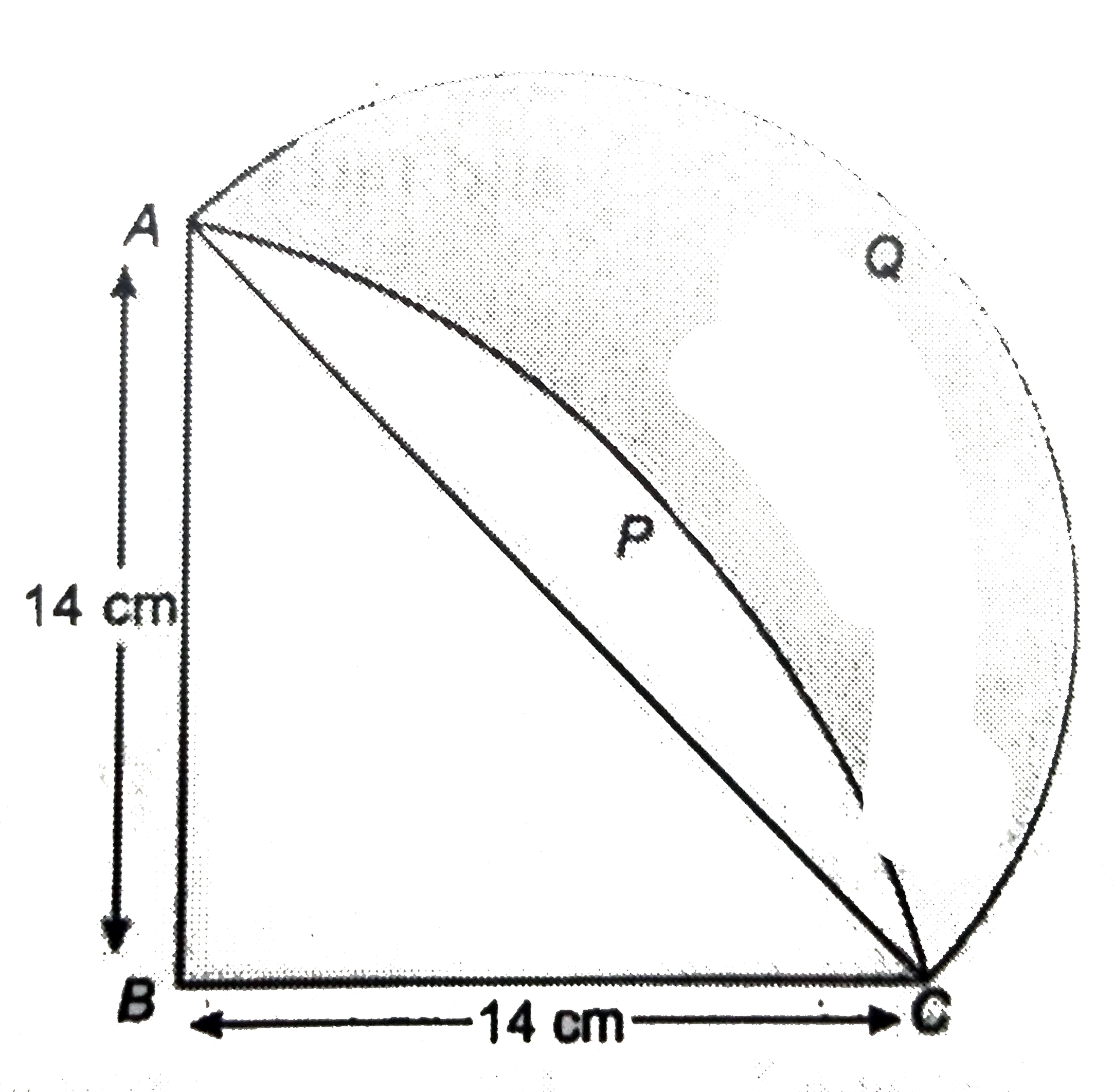
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn Fig. 15.98, ABC is a right angled triangle in which ∠A=90o , AB=21 cm and AC=28 cm . Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region. (FIGURE)
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIn Figure ABCD is a square with side 7 cm. A circle is drawn circumscribing the square . Find the area of the shaded region .

View Solution
