AB is a diameter of a circle with centre O, AH and BK are perpendiculars from A and B to the tangent at a point P on the circle, Prove that AH+BK=AB.

Step by step video & image solution for AB is a diameter of a circle with centre O, AH and BK are perpendiculars from A and B to the tangent at a point P on the circle, Prove that AH+BK=AB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle. AHandBK are perpendiculars from A and B respectively to the tangent at P Prove that AH+BK=AB.
View SolutionAB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that ∠POQ=90∘
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
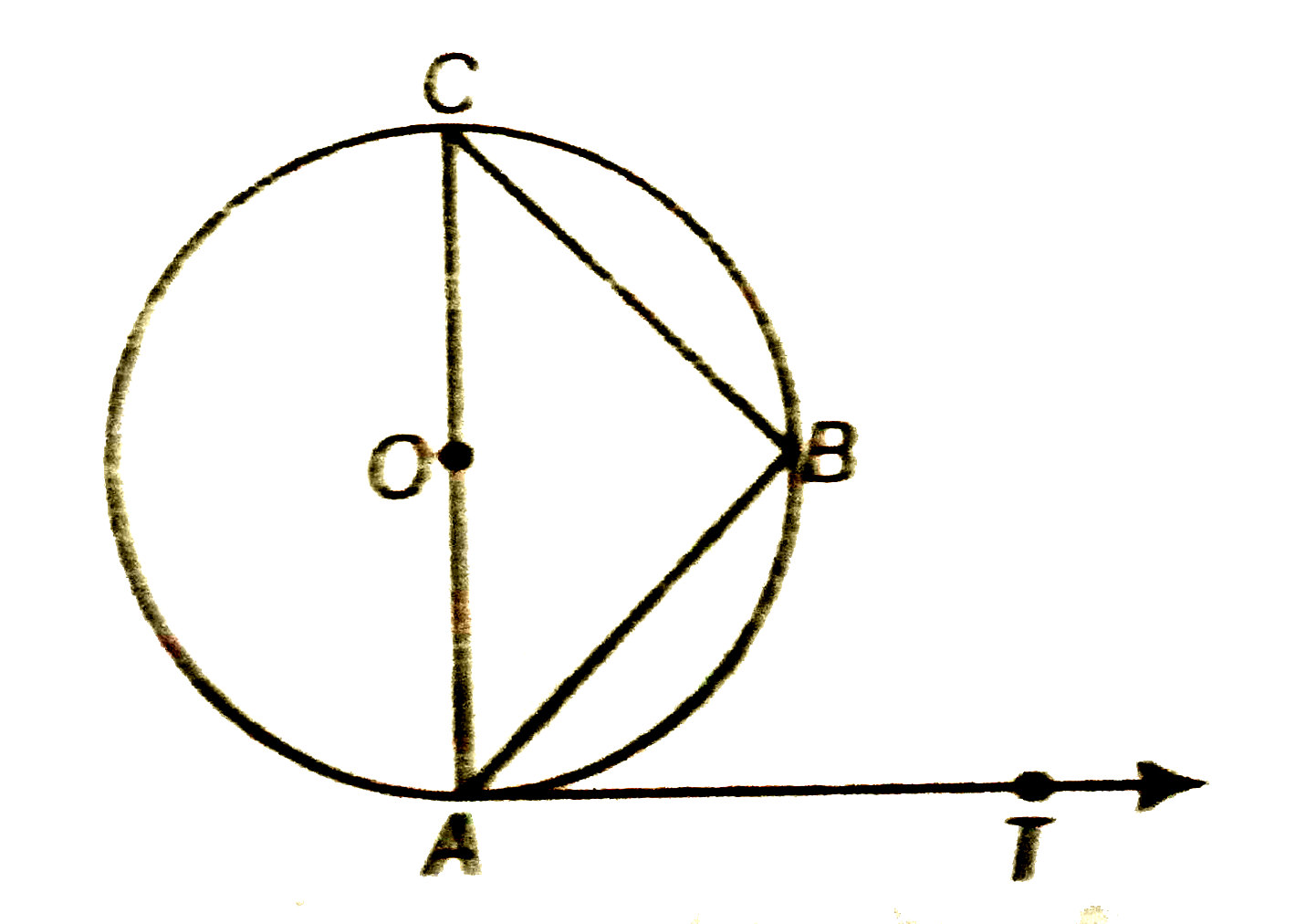
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
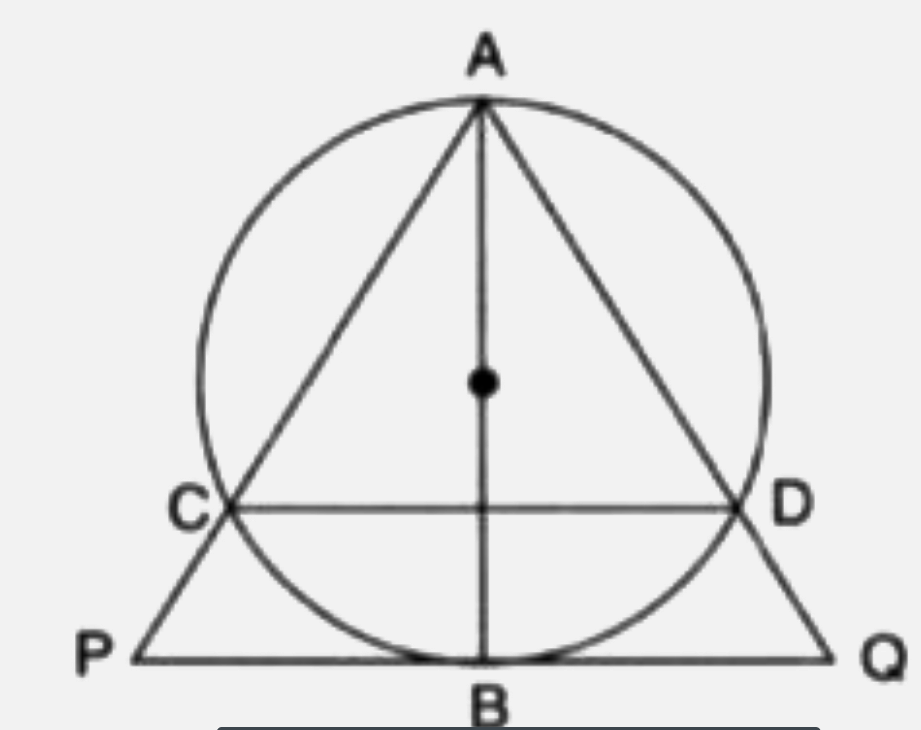
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
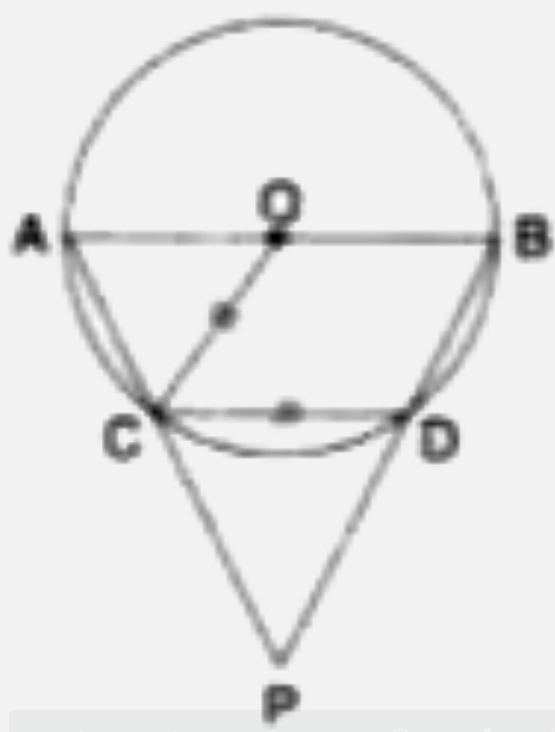
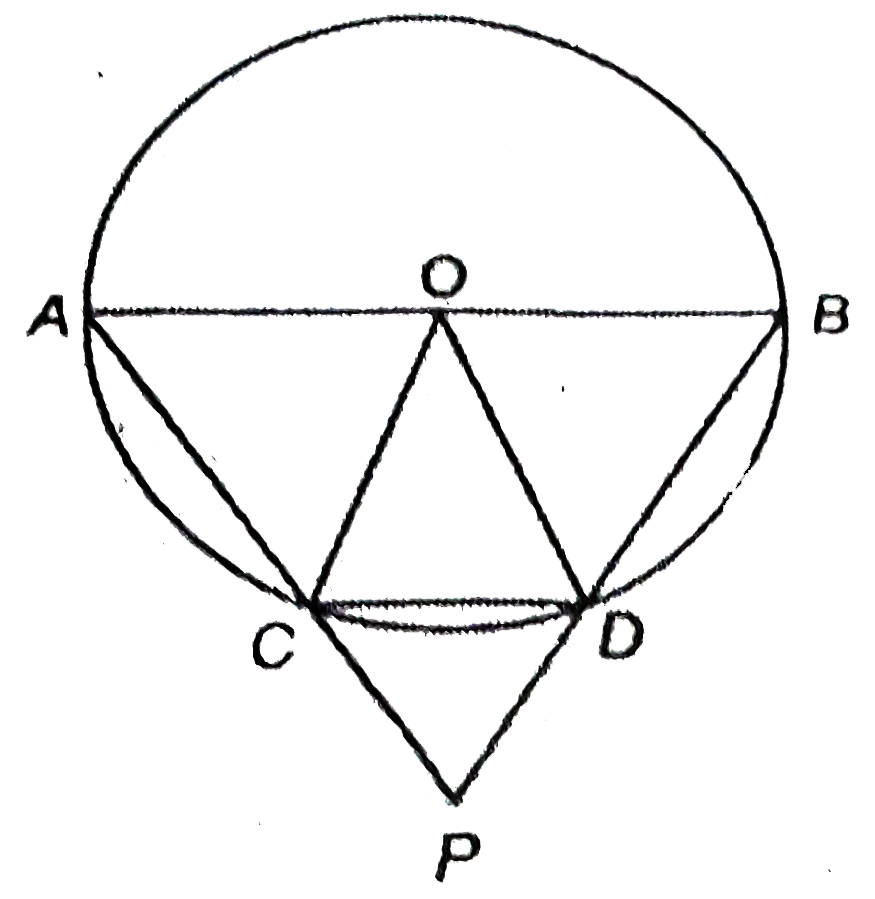
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
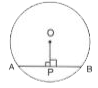
View SolutionThe following figure shows a circle with centre O.
If OP is perpendicular to AB, prove that AP = BP.
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View Solution