If AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
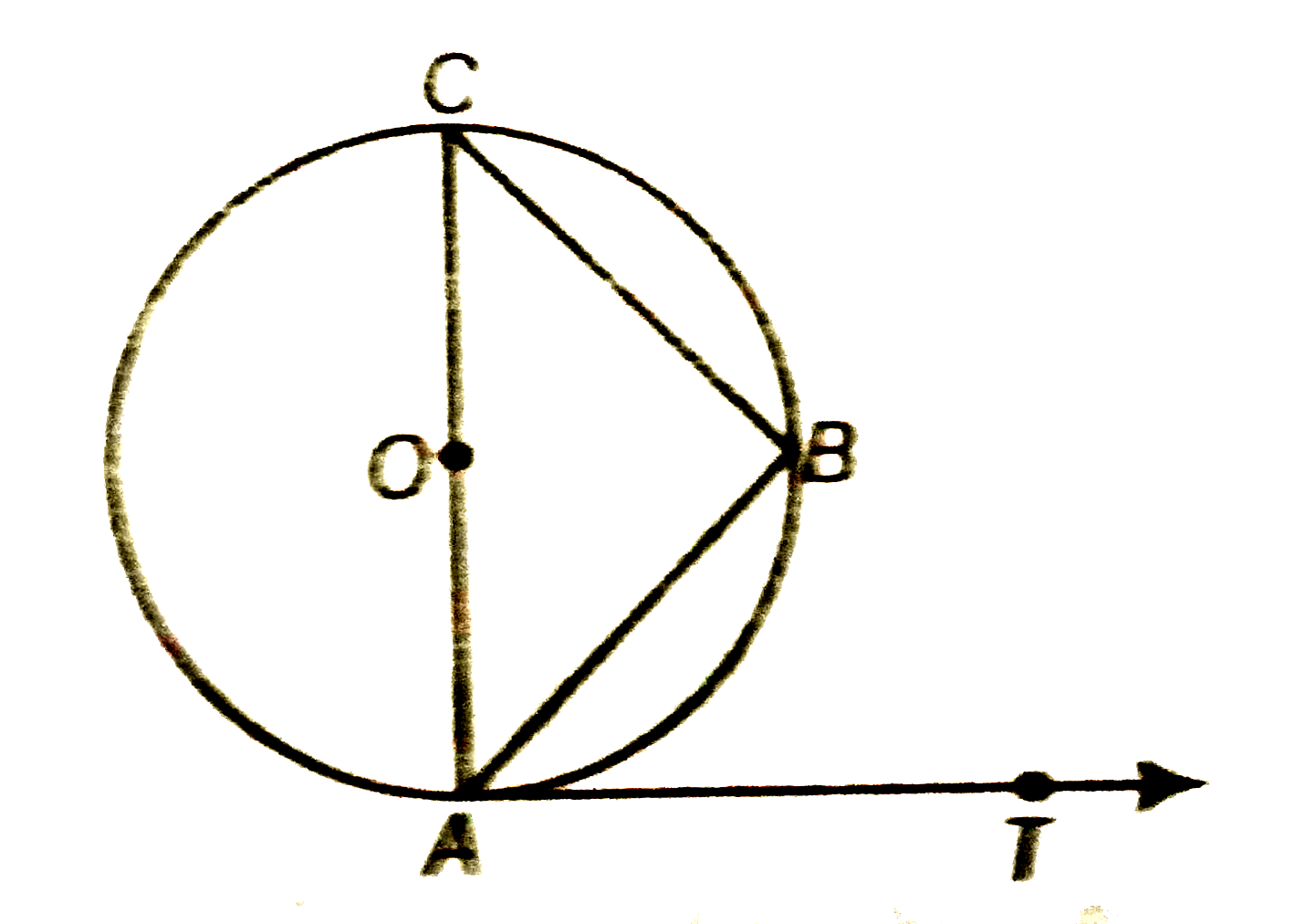
Since, AC is diameter line, so angle in semi-circle makes an angle 90∘
∴∠ABC=90∘ [by property]
In ΔABC, ∠CAB+∠ABC+∠ACB=180∘
[:'sum of all interior angles of any triangle is 180∘]
⇒∠CAB+∠ACB=180∘−90∘=90∘......(i)
Since, diameter of a circle is perpendicular to the tengent.
i.e., CA⊥AT
∴∠CAT=90∘
⇒∠CAB+∠BAT=90∘.....(ii)
From Eqs. (i) and (ii).
∠CAB+∠ACB=∠CAB+∠BAT
⇒∠ACB=∠BAT
Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Prove that the diameter is the greatest chord in a circle.
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
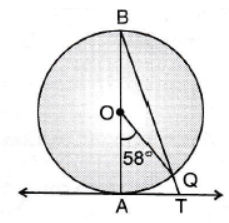 View Solution
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
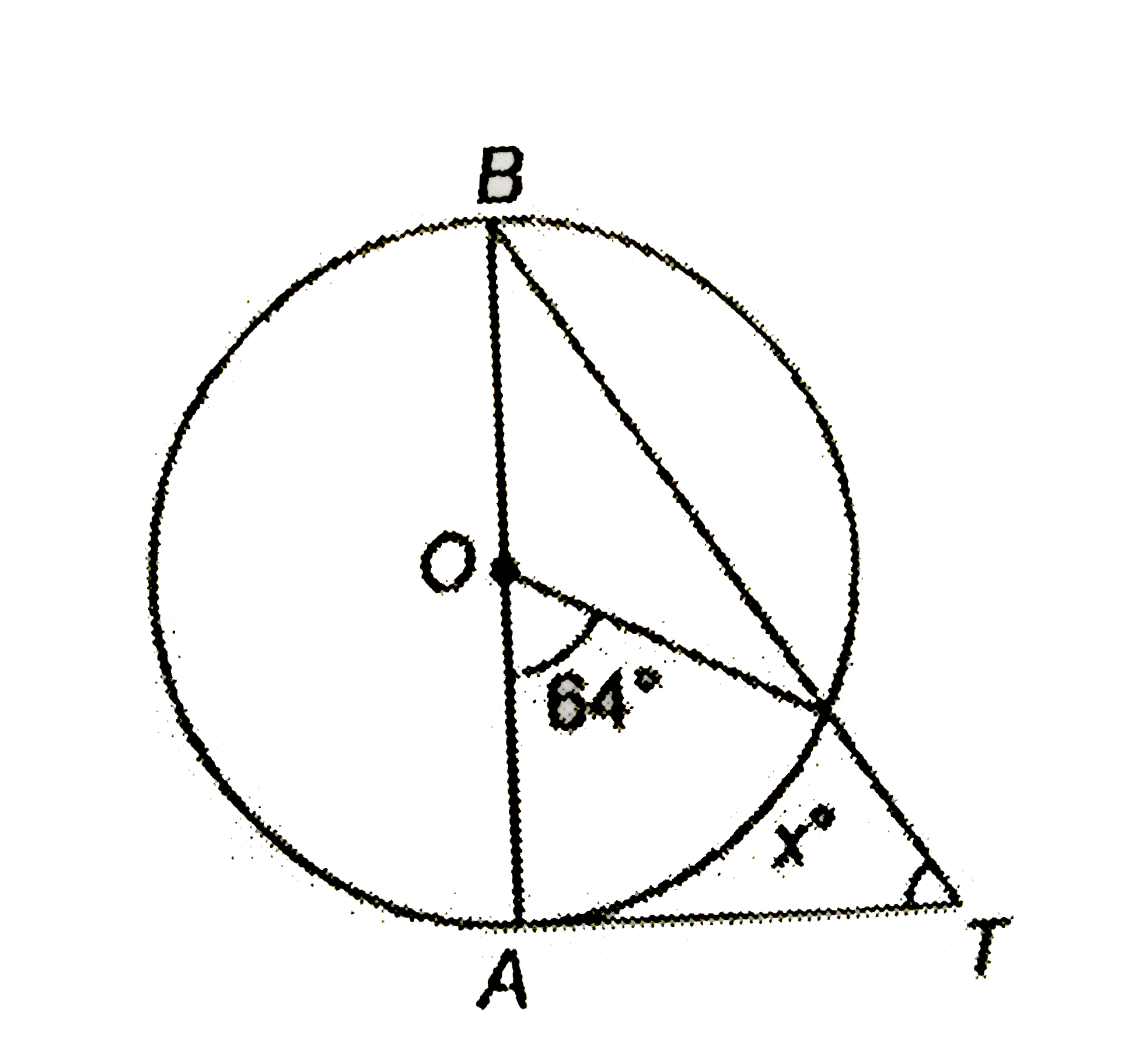 View Solution
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.
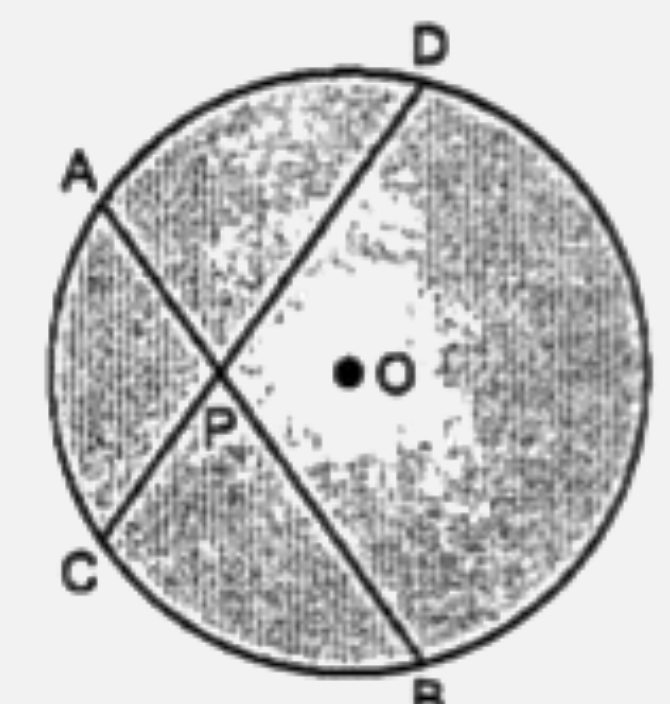
Prove that:
BP=DPView SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
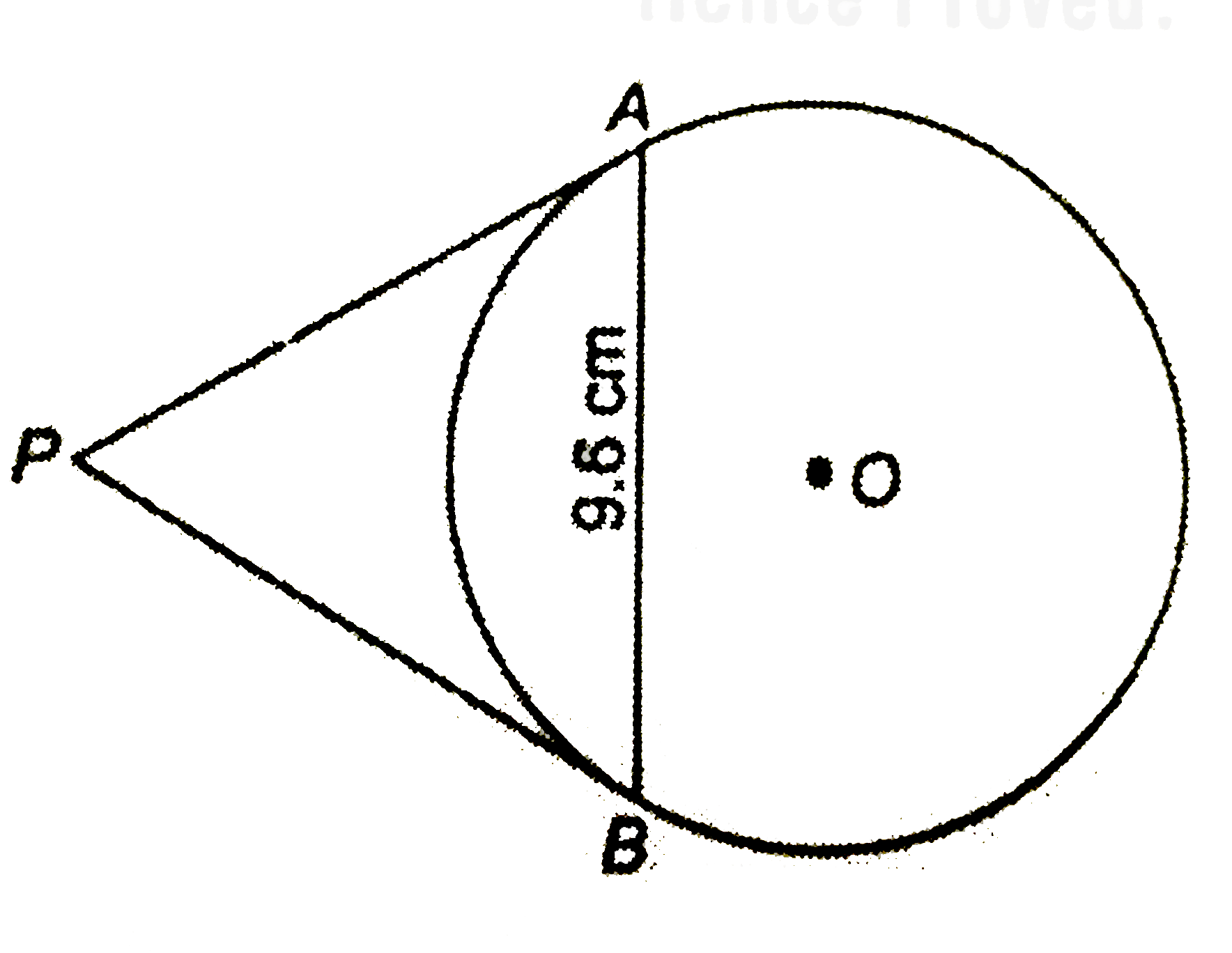 View Solution
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
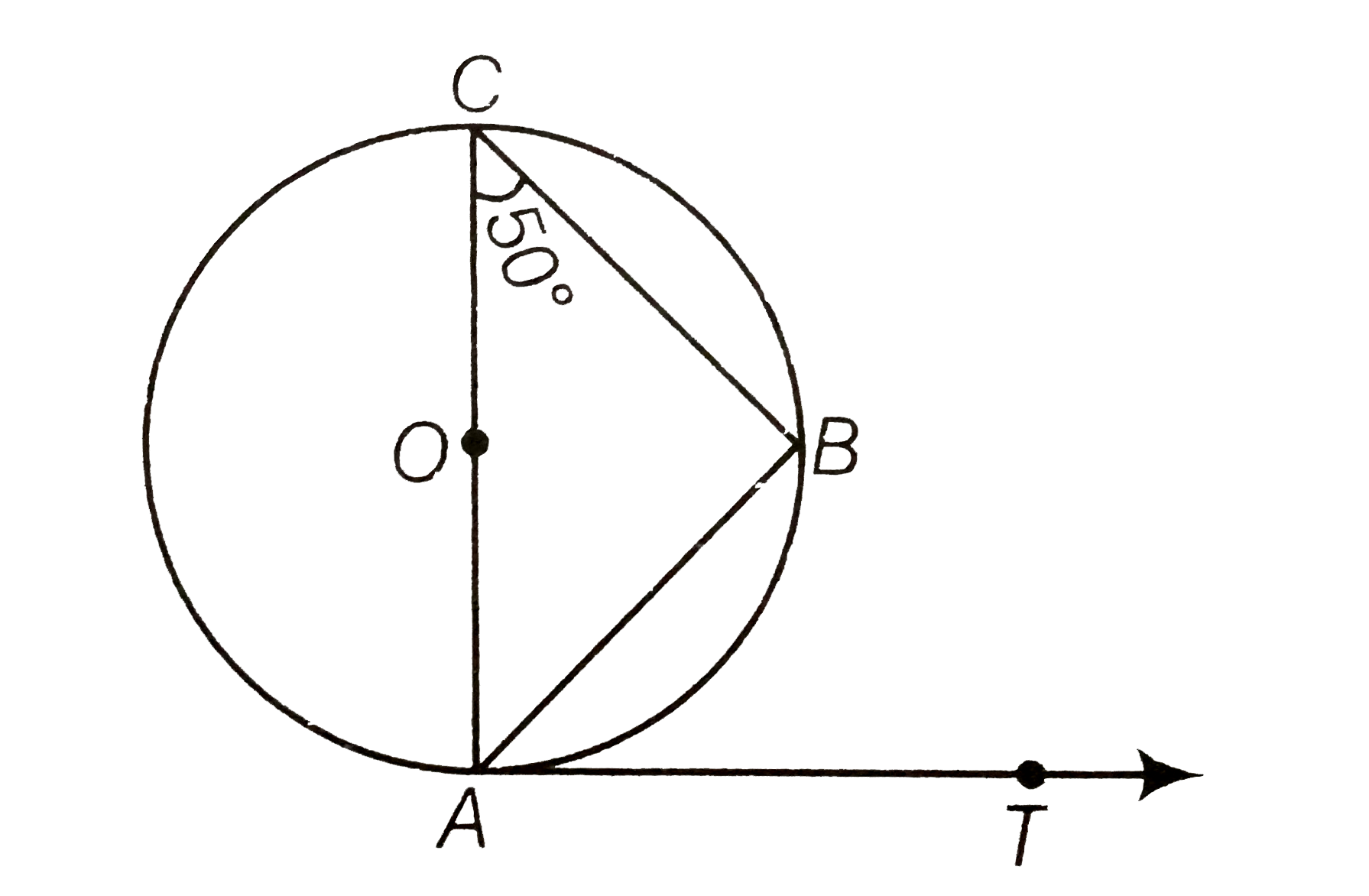 View Solution
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
 View Solution
View Solution

