The midpoint P of the line segment joining the points A(-10, 4) and B(-2, 0) lies on the line segment joining the points C(-9, -4) and D(-4, y). Find the ratio in which P divides CD. Also find the value of y.
To solve the problem, we need to find the midpoint P of the line segment joining points A(−10,4) and B(−2,0), and then determine the ratio in which P divides the line segment CD where C(−9,−4) and D(−4,y). We will also find the value of y.
Step 1: Find the midpoint P of segment AB
The formula for the midpoint P(x,y) of a line segment joining points A(x1,y1) and B(x2,y2) is given by:
P=(x1+x22,y1+y22)
Substituting the coordinates of points A(−10,4) and B(−2,0):
P=(−10+(−2)2,4+02)=(−122,42)=(−6,2)
Step 2: Use the section formula to find the ratio in which P divides CD
Let the ratio in which P divides CD be k:1. According to the section formula, the coordinates of point P can be expressed as:
P=(k⋅x2+1⋅x1k+1,k⋅y2+1⋅y1k+1)
Here, C(−9,−4) and D(−4,y) give us x1=−9, y1=−4, x2=−4, and y2=y. Thus, we can write:
(−6,2)=(k⋅(−4)+1⋅(−9)k+1,k⋅y+1⋅(−4)k+1)
Step 3: Solve for k using the x-coordinate
From the x-coordinate:
−6=k⋅(−4)−9k+1
Multiplying both sides by k+1:
−6(k+1)=−4k−9
Expanding and rearranging gives:
−6k−6=−4k−9
−6k+4k=−9+6
−2k=−3
k=32
Step 4: Find the ratio
The ratio in which P divides CD is k:1=32:1 or 3:2.
Step 5: Solve for y using the y-coordinate
Now, using the y-coordinate:
2=k⋅y−4k+1
Substituting k=32:
2=32y−432+1=32y−452
Multiplying both sides by 52:
2⋅52=32y−4
5=32y−4
5+4=32y
9=32y
y=9⋅23=6
Final Answer
The ratio in which P divides CD is 3:2 and the value of y is 6.
−6k+4k=−9+6
−2k=−3
k=32
5=32y−4
5+4=32y
9=32y
y=9⋅23=6
Topper's Solved these Questions
Similar Questions
The point P(-4,2) lies on the line segment joining the points A(-4,6) and B (-4,-6).
View SolutionPoint (x,4) lies on the line segment joining the points A (-5, 8) and B (4,-10) Find the ratio in which point P divides the line segment AB. Also find the value of x?
View SolutionShow that the point P(−4,2) lies on the line segment joining the points A(−4,6) and B(−4,−6).
View SolutionFind k so that the point P(−4, 6) lies on the line segment joining A(k, 10) and B(3, −8) . Also, find the ratio in which P divides AB
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
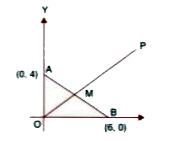
co-ordinates of P
View SolutionIf the point P(2,1)lies on the line segment joining points A(4,2)and B(8,4), then
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
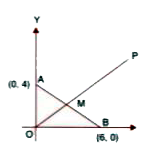
co-ordinates of M
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
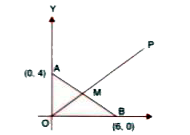
length of BP
View SolutionFind the ratio in which the points
Q(-1,-8) divide the line segment joining the points A(1,-2) and B(4,7).
View SolutionFind the ratio in which the point (−3, p) divides the line segment joining the points (−5, −4) and (−2, 3) . Hence, find the value of p .
View Solution
