Calculate the mean deviation about median age for the age distribution of 100 persons given below: Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55 Number 5 6 12 14 26 12 16 9
To calculate the mean deviation about the median age for the given age distribution of 100 persons, we will follow these steps:
Step 1: Create a Continuous Frequency Distribution Table
To convert the age groups into continuous intervals, we will adjust the boundaries by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit.
| Age Group | Frequency (f_i) |
|-------------|------------------|
| 15.5 - 20.5 | 5 |
| 20.5 - 25.5 | 6 |
| 25.5 - 30.5 | 12 |
| 30.5 - 35.5 | 14 |
| 35.5 - 40.5 | 26 |
| 40.5 - 45.5 | 12 |
| 45.5 - 50.5 | 16 |
| 50.5 - 55.5 | 9 |
Step 2: Calculate the Cumulative Frequency (cf)
Now, we will calculate the cumulative frequency for the frequency distribution.
| Age Group | Frequency (f_i) | Cumulative Frequency (cf) |
|-------------|------------------|---------------------------|
| 15.5 - 20.5 | 5 | 5 |
| 20.5 - 25.5 | 6 | 11 |
| 25.5 - 30.5 | 12 | 23 |
| 30.5 - 35.5 | 14 | 37 |
| 35.5 - 40.5 | 26 | 63 |
| 40.5 - 45.5 | 12 | 75 |
| 45.5 - 50.5 | 16 | 91 |
| 50.5 - 55.5 | 9 | 100 |
Step 3: Find the Median
The median is the value that divides the distribution into two equal halves. Since the total frequency (N) is 100, the median position is at N/2 = 50.
From the cumulative frequency table, the 50th term lies in the age group 35.5 - 40.5.
Step 4: Calculate the Midpoint (x_i)
Next, we will calculate the midpoints for each age group.
| Age Group | Midpoint (x_i) |
|-------------|-----------------|
| 15.5 - 20.5 | 18 |
| 20.5 - 25.5 | 23 |
| 25.5 - 30.5 | 28 |
| 30.5 - 35.5 | 33 |
| 35.5 - 40.5 | 38 |
| 40.5 - 45.5 | 43 |
| 45.5 - 50.5 | 48 |
| 50.5 - 55.5 | 53 |
Step 5: Calculate the Mean Deviation
We will calculate the deviation from the median (38) for each midpoint and then multiply by the frequency.
| Age Group | Midpoint (x_i) | f_i | x_i - m | f_i * (x_i - m) |
|-------------|-----------------|-----|---------|------------------|
| 15.5 - 20.5 | 18 | 5 | -20 | -100 |
| 20.5 - 25.5 | 23 | 6 | -15 | -90 |
| 25.5 - 30.5 | 28 | 12 | -10 | -120 |
| 30.5 - 35.5 | 33 | 14 | -5 | -70 |
| 35.5 - 40.5 | 38 | 26 | 0 | 0 |
| 40.5 - 45.5 | 43 | 12 | 5 | 60 |
| 45.5 - 50.5 | 48 | 16 | 10 | 160 |
| 50.5 - 55.5 | 53 | 9 | 15 | 135 |
Now, we sum the last column:
Sum of fi⋅(xi−m)=−100−90−120−70+0+60+160+135=−25
Step 6: Calculate the Mean Deviation
The mean deviation (MD) is calculated using the formula:
MD=∑(fi⋅(xi−m))∑fi=−25100=−0.25
Final Result
The mean deviation about the median age is 0.25 (ignoring the sign, as mean deviation is typically reported as a positive value).
To convert the age groups into continuous intervals, we will adjust the boundaries by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit.
|-------------|------------------|
| 15.5 - 20.5 | 5 |
| 20.5 - 25.5 | 6 |
| 25.5 - 30.5 | 12 |
| 30.5 - 35.5 | 14 |
| 35.5 - 40.5 | 26 |
| 40.5 - 45.5 | 12 |
| 45.5 - 50.5 | 16 |
| 50.5 - 55.5 | 9 |
Now, we will calculate the cumulative frequency for the frequency distribution.
|-------------|------------------|---------------------------|
| 15.5 - 20.5 | 5 | 5 |
| 20.5 - 25.5 | 6 | 11 |
| 25.5 - 30.5 | 12 | 23 |
| 30.5 - 35.5 | 14 | 37 |
| 35.5 - 40.5 | 26 | 63 |
| 40.5 - 45.5 | 12 | 75 |
| 45.5 - 50.5 | 16 | 91 |
| 50.5 - 55.5 | 9 | 100 |
The median is the value that divides the distribution into two equal halves. Since the total frequency (N) is 100, the median position is at N/2 = 50.
Next, we will calculate the midpoints for each age group.
|-------------|-----------------|
| 15.5 - 20.5 | 18 |
| 20.5 - 25.5 | 23 |
| 25.5 - 30.5 | 28 |
| 30.5 - 35.5 | 33 |
| 35.5 - 40.5 | 38 |
| 40.5 - 45.5 | 43 |
| 45.5 - 50.5 | 48 |
| 50.5 - 55.5 | 53 |
We will calculate the deviation from the median (38) for each midpoint and then multiply by the frequency.
|-------------|-----------------|-----|---------|------------------|
| 15.5 - 20.5 | 18 | 5 | -20 | -100 |
| 20.5 - 25.5 | 23 | 6 | -15 | -90 |
| 25.5 - 30.5 | 28 | 12 | -10 | -120 |
| 30.5 - 35.5 | 33 | 14 | -5 | -70 |
| 35.5 - 40.5 | 38 | 26 | 0 | 0 |
| 40.5 - 45.5 | 43 | 12 | 5 | 60 |
| 45.5 - 50.5 | 48 | 16 | 10 | 160 |
| 50.5 - 55.5 | 53 | 9 | 15 | 135 |
The mean deviation (MD) is calculated using the formula:
The mean deviation about the median age is 0.25 (ignoring the sign, as mean deviation is typically reported as a positive value).
Topper's Solved these Questions
Similar Questions
Calculate the mean deviatioin about median age for the age distribution of 100 persons given below:
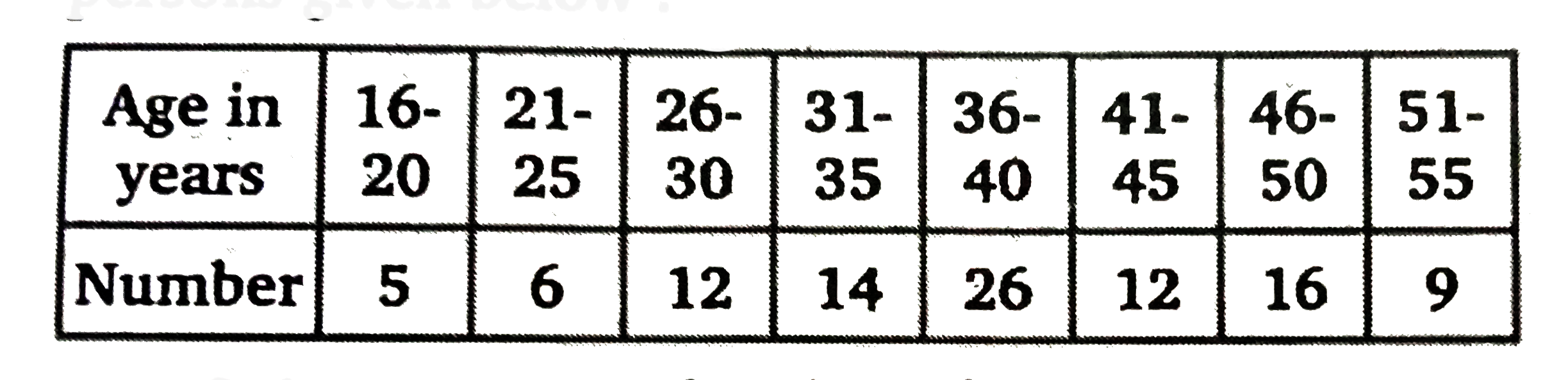
View SolutionCalculate the mean deviation about the median of the following frequency distribution: 5 7 9 11 13 15 17 Having Frequency 2 4 6 8 10 12 8
View SolutionCalculate mean deviation from the median for the following distribution: xi: 10 15 20 25 30 35 40 45 fi: 7 3 8 5 6 8 4 9
View SolutionCalculate the mean deviation about the mean for the following frequency distribution Class interval 0−4,4−8,8−12,12−16,16−20 Frequency 4,6,8,5,2
View SolutionFind the Mean deviation (about Mean) of the following observation 2,3,5,6,9,10,12,17,20,26.
View SolutionCalculate the mean and standard deviation for the following table given the age distribution of a group of people: Age: 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of persons: 3 51 122 141 130 51 2
View SolutionCalculate the mean and standard deviation for the following table given the age distribution of a group of people: Age: 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of persons: 3 51 122 141 130 51 2
View SolutionCalculate mean deviation from the median for the following distribution: xi: , 10, 15, 20, 25, 30, 35, 40, 45 fi: , 7, 3, 8, 5, 6, 8, 4, 9
View SolutionFind the mean deviation about the median of the following frequency distribution: Class:, 0-6, 6-12, 12-18, 18-24, 24-30 Frequency:, 8, 10, 12, 9, 5
View SolutionFind the mean deviation about the median of the following frequency distribution: Class:, 0-6, 6-12, 12-18, 18-24, 24-30 Frequency:, 8, 10, 12, 9, 5
View Solution
