Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
To determine the length of AD in terms of b and c using the Pythagorean theorem, we can follow these steps:
Step 1: Identify the triangles
We have triangle ABC where AB=c and AC=b. The point D lies on AC.
Step 2: Apply the Pythagorean theorem in triangle ABC
According to the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=c2+b2(1)
Step 3: Analyze triangles ABD and CBA
Since ∠ABD=∠CBA (common angle) and ∠ADB=∠CAB=90∘, we can conclude that triangles ABD and CBA are similar by the AA criterion of similarity.
Step 4: Set up the ratio of corresponding sides
From the similarity of triangles ABD and CBA:
ABCB=ADCA
Substituting the known lengths:
cCB=ADb
Step 5: Express CB in terms of b and c
From equation (1), we know:
CB=√c2+b2
Substituting this into our ratio:
c√c2+b2=ADb
Step 6: Solve for AD
Cross-multiplying gives:
c⋅b=AD⋅√c2+b2
Now, isolating AD:
AD=c⋅b√c2+b2
Final Result
Thus, the length of AD in terms of b and c is:
AD=bc√c2+b2
We have triangle ABC where AB=c and AC=b. The point D lies on AC.
According to the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=c2+b2(1)
Since ∠ABD=∠CBA (common angle) and ∠ADB=∠CAB=90∘, we can conclude that triangles ABD and CBA are similar by the AA criterion of similarity.
From the similarity of triangles ABD and CBA:
ABCB=ADCA
Substituting the known lengths:
cCB=ADb
From equation (1), we know:
CB=√c2+b2
Substituting this into our ratio:
c√c2+b2=ADb
Cross-multiplying gives:
c⋅b=AD⋅√c2+b2
Now, isolating AD:
AD=c⋅b√c2+b2
Thus, the length of AD in terms of b and c is:
AD=bc√c2+b2
Topper's Solved these Questions
Similar Questions
Knowledge Check
Select the option that correctly identifies the different genera (A,B,C and D) of kingdom Fungi shown in figure.
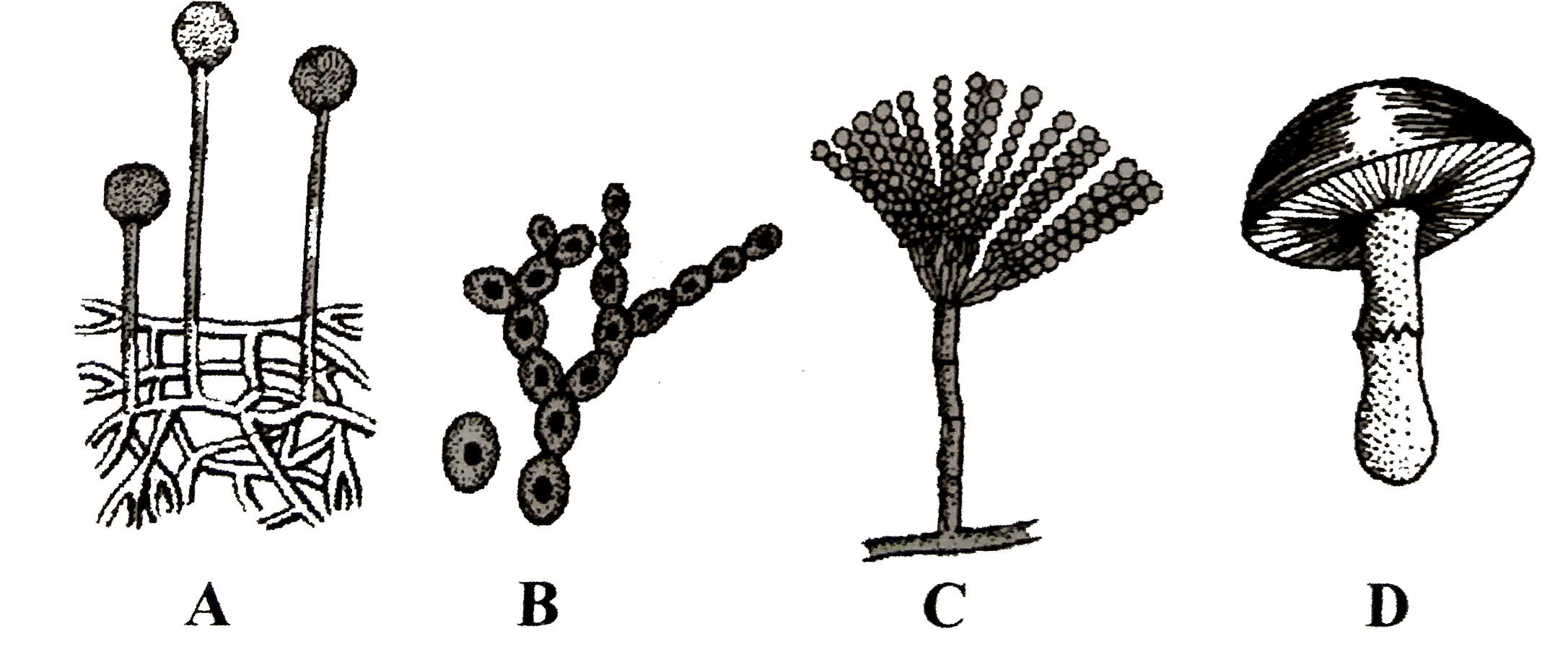 AABCDMucorSaccharomyceMorchellaAmanitaBABCDMucorSaccharomycesAspergillusMorchellaCABCDRhizopusSaccharomycesAspergiliusMorchellaDABCDAspergillusRhizopusPeniciliumAgaricus
AABCDMucorSaccharomyceMorchellaAmanitaBABCDMucorSaccharomycesAspergillusMorchellaCABCDRhizopusSaccharomycesAspergiliusMorchellaDABCDAspergillusRhizopusPeniciliumAgaricusThe Boolean expression of the output y in terms of the input A and B for the circuit shown in figure.
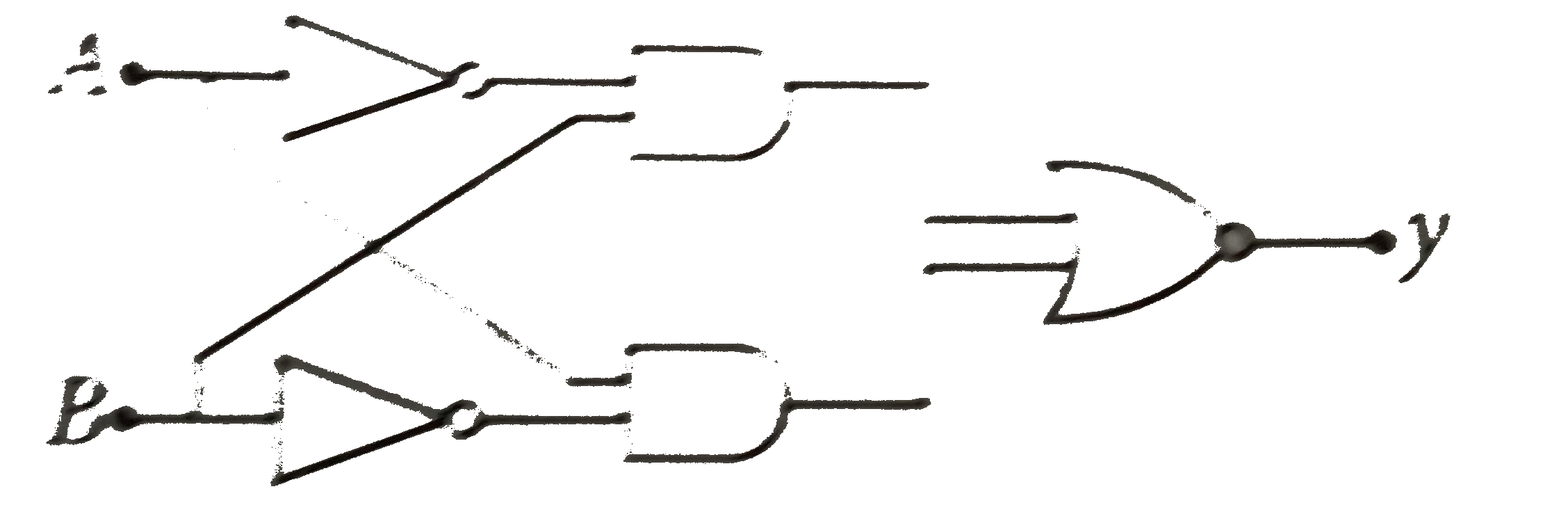 A¯¯¯AB+A¯¯¯BBABCAB+¯¯¯A¯¯¯BDA¯¯¯B+1
A¯¯¯AB+A¯¯¯BBABCAB+¯¯¯A¯¯¯BDA¯¯¯B+1
Write down the co-ordinates of each points A,B,C,D,E and F as shown in following figure.

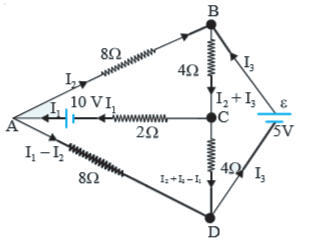
View SolutionUsing Kirchhoff ' s rules , calculate the potential difference between B and D in the circuit diagram as shown in the figure.

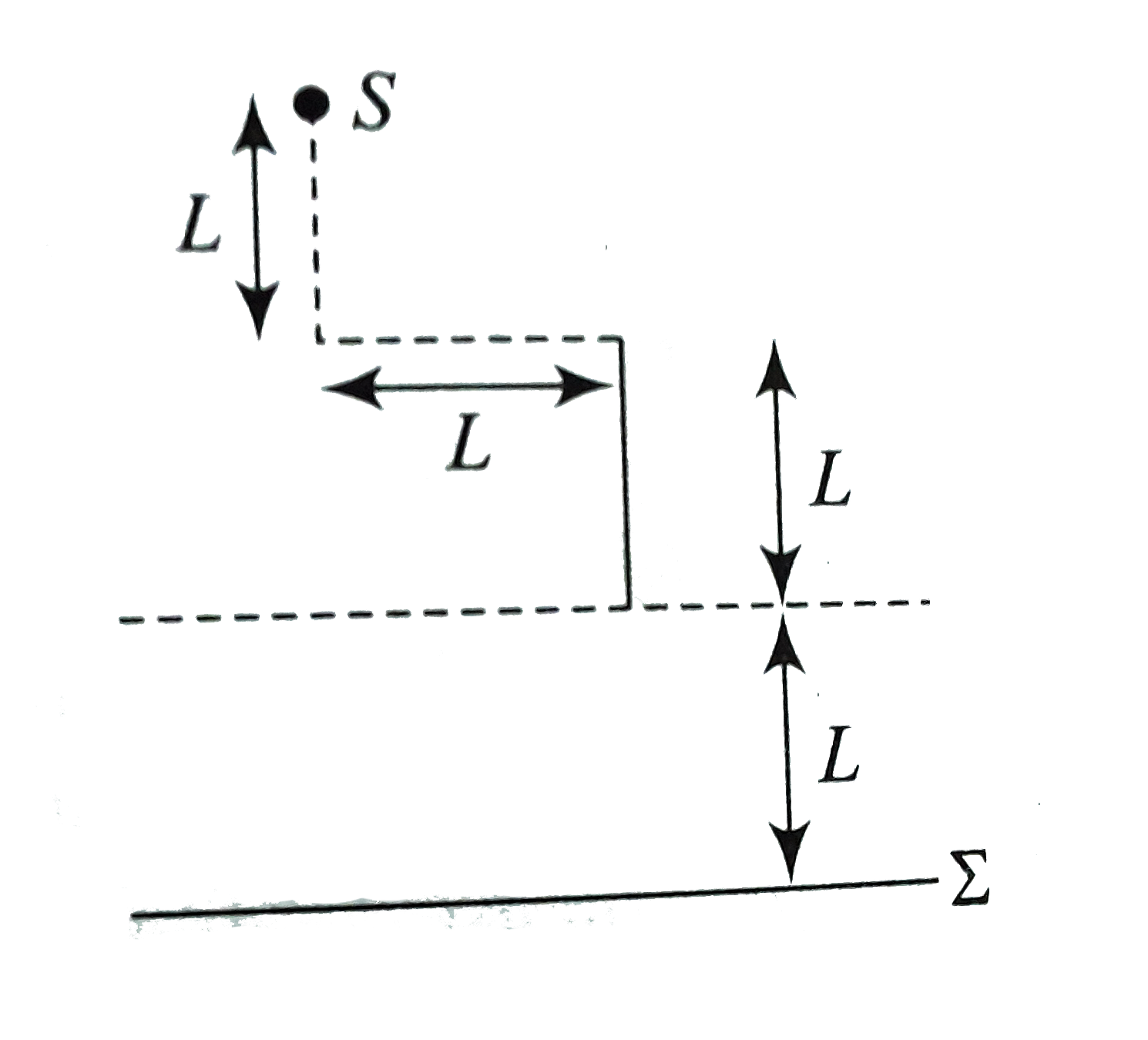
View SolutionA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
View SolutionWithout using Pythagoras theorem, show that the points A(2,1), B(5,4) and C(3,6) are the vertices of a right-angled triangle.
View SolutionWithout using the Pythagoras theorem, show that the points (4,4), (3,5)and (1,1)are the vertices of a right angled triangle.
View SolutionUse Kirchhoff's rules to determine the potential differnce between the poits A and D when no current flows in the arm BE of the electric network shown in figure
View Solution