In Figure, show that AB∣∣EF
To prove that lines AB and EF are parallel, we will use the properties of angles formed by a transversal intersecting two lines. Here’s the step-by-step solution:
Step 1: Identify Given Angles
We are given the following angles:
- ∠CAB=57∘
- ∠ECD=35∘
- ∠ACI=22∘
- ∠CEF=145∘
Step 2: Find ∠ACD
We know that:
∠ACD=∠ACE+∠ECD
Substituting the values:
∠ACD=22∘+35∘=57∘
Step 3: Establish Relationship Between Angles
Since ∠BAC=∠ACD (both equal 57∘), we have:
∠BAC=∠ACD
This indicates that AB and CD are cut by the transversal BC.
Step 4: Apply the Corresponding Angles Postulate
According to the Corresponding Angles Postulate, if two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel. Here, since:
∠ABC=∠BCD=57∘
we can conclude that:
AB∥CD
Step 5: Find ∠DCE
Now, we will check the angles on the other side of the transversal CE:
∠DCE+∠CEF=180∘
Substituting the values:
35∘+145∘=180∘
This shows that the angles are supplementary.
Step 6: Conclude CD∥EF
Since the sum of the interior angles on the same side of the transversal CE is 180∘, we conclude that:
CD∥EF
Step 7: Combine Results
From Steps 4 and 6, we have:
- AB∥CD
- CD∥EF
By the transitive property of parallel lines, we conclude:
AB∥EF
Final Conclusion
Thus, we have shown that AB is parallel to EF.
---
We are given the following angles:
- ∠CAB=57∘
- ∠ECD=35∘
- ∠ACI=22∘
- ∠CEF=145∘
We know that:
∠ACD=∠ACE+∠ECD
Substituting the values:
∠ACD=22∘+35∘=57∘
Since ∠BAC=∠ACD (both equal 57∘), we have:
∠BAC=∠ACD
This indicates that AB and CD are cut by the transversal BC.
According to the Corresponding Angles Postulate, if two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel. Here, since:
∠ABC=∠BCD=57∘
we can conclude that:
AB∥CD
Now, we will check the angles on the other side of the transversal CE:
∠DCE+∠CEF=180∘
Substituting the values:
35∘+145∘=180∘
This shows that the angles are supplementary.
Since the sum of the interior angles on the same side of the transversal CE is 180∘, we conclude that:
CD∥EF
From Steps 4 and 6, we have:
- AB∥CD
- CD∥EF
AB∥EF
Thus, we have shown that AB is parallel to EF.
Topper's Solved these Questions
Similar Questions
In Figure, Show that AB ∣∣ EF.
View SolutionIn the given figure, show that AB∣∣EF.
View SolutionIn Figure, it is given that AB=EF, BC=DE, AB ⊥BD and FE ⊥CE. Prove that ABD ≅FEC.
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
View SolutionIn Figure, it is given that AB=CF,EF=BD and ∠AFE=∠CBD. Prove that AFE≅CBD.
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE ≅CBD
View SolutionIn Figure, if AB∣∣CD, EF ⊥CD and ∠GED=1260, find ∠AGE, ∠GEF and ∠FGE
View SolutionIn Figure shows the graph of f(x), what is the value of f(f(3)) ?
View SolutionIn Figure, if AB||CD, EF||BC, ∠BAC=65∘ and ∠DHF=35∘, find ∠AGH.
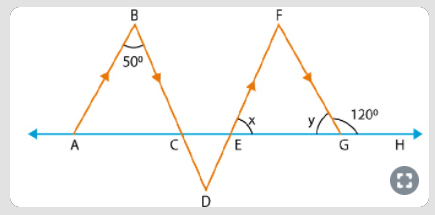
View SolutionIn Figure, if AB∣∣DF and BD∣∣FG such that ∠FGH=120∘ and ∠B=50∘, find x and y.
View Solution