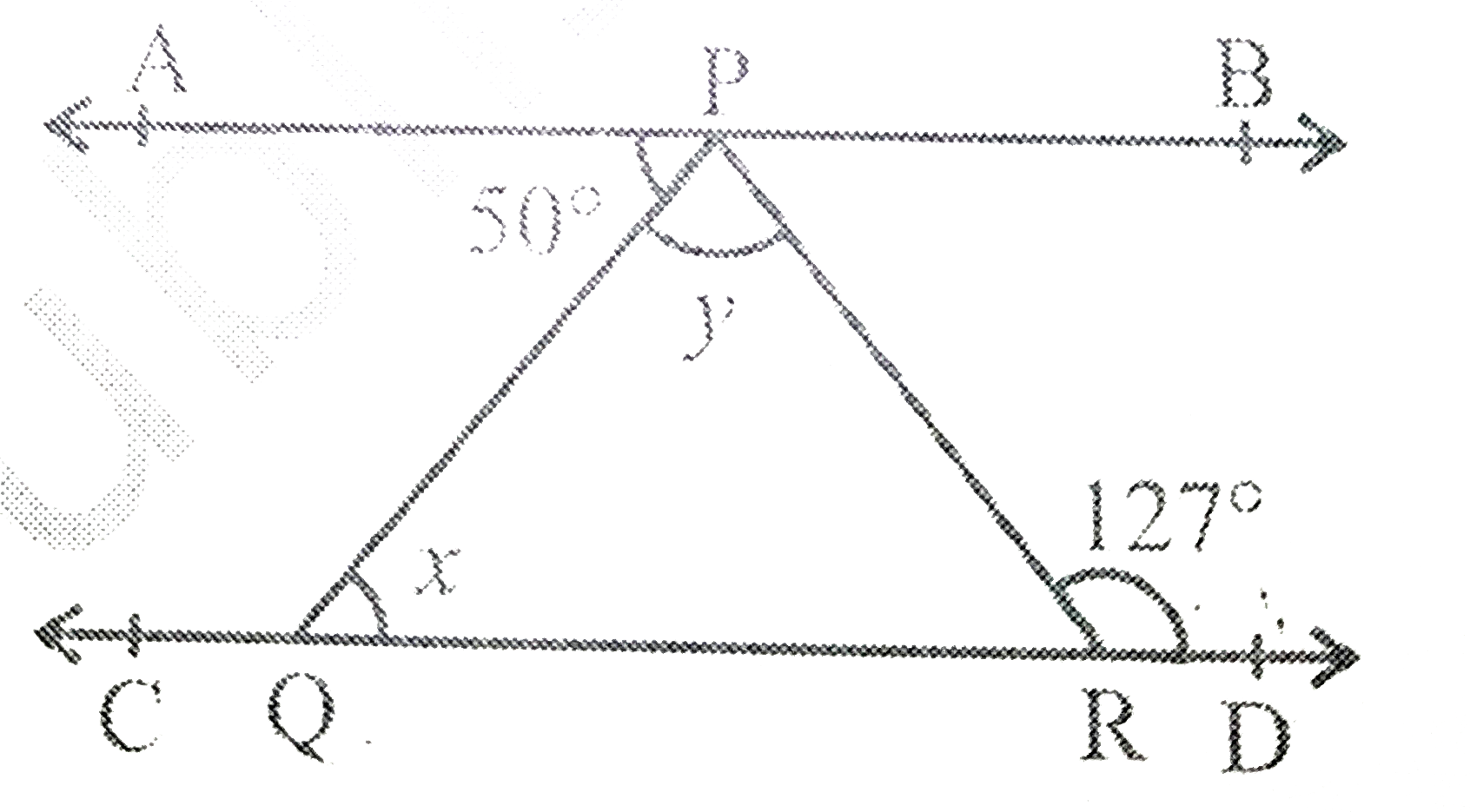
In Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
To solve the problem, we need to find the values of angles x and y given the conditions in the figure. Here’s the step-by-step solution:
Step 1: Identify the Given Information
- We have two parallel lines AB and CD.
- The angle ∠APQ=50∘.
- The angle ∠PRD=127∘.
Step 2: Use the Properties of Parallel Lines
Since AB is parallel to CD and PQ is a transversal, we can use the property of alternate interior angles.
Step 3: Find Angle x
- The angle ∠APQ corresponds to ∠PQR (which is x).
- According to the alternate interior angles theorem, since AB∥CD, we have:
∠APQ=∠PQR
- Therefore, we can conclude:
x=50∘
Step 4: Find Angle y
- Now, we look at the angles formed by the transversal PR with the parallel lines AB and CD.
- The angle ∠APR is equal to ∠PRD because they are corresponding angles.
- Given that ∠PRD=127∘, we have:
∠APR=y
- Therefore, we can conclude:
y=127∘
Final Answer
- The values are:
x=50∘,y=127∘
- We have two parallel lines AB and CD.
- The angle ∠APQ=50∘.
- The angle ∠PRD=127∘.
Since AB is parallel to CD and PQ is a transversal, we can use the property of alternate interior angles.
- The angle ∠APQ corresponds to ∠PQR (which is x).
- According to the alternate interior angles theorem, since AB∥CD, we have:
∠APQ=∠PQR
- Therefore, we can conclude:
x=50∘
- Now, we look at the angles formed by the transversal PR with the parallel lines AB and CD.
- The angle ∠APR is equal to ∠PRD because they are corresponding angles.
- Given that ∠PRD=127∘, we have:
∠APR=y
- Therefore, we can conclude:
y=127∘
- The values are:
x=50∘,y=127∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.32, if AB∣∣CD,∠APQ=50∘and∠PRD=127∘, find x and y.
View SolutionIn Figure, if QT⊥PR, ∠TQR=40∘ and ∠SPR=30∘, find x and y.
View SolutionIn Figure, AB=AC and ∠ACD=1000, find ∠BAC
View SolutionIn Figure, if ∠ACB=40∘, ∠DPB=120∘, find ∠CBD
View SolutionIn Figure, AB=AC and ∠ACD=1200. Find ∠A
View SolutionIn Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
View SolutionIn Figure, if ∠AOB=800and ∠ABC=300, then find ∠CAO
View SolutionIn Figure, ∠BAD=780, ∠DCF=x0and ∠DEF=y0. Find the value of x and y
View SolutionIn Figure, if PQ⊥PS, PQSR, ∠SQR=280and ∠QRT=650, then find the values of x and y
View SolutionIn Figure, if ∠BAC=600 and ∠BCA=200, find ∠ADC
View Solution
