If the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
To prove that the given lines PQ and RS are parallel when the bisectors of a pair of alternate angles formed by a transversal are parallel, we can follow these steps:
1. Draw the Diagram:
- Let PQ and RS be two lines cut by a transversal AB.
- Identify the alternate angles formed by the transversal. Let ∠PAB and ∠RBA be the alternate angles.
2. Identify the Bisectors:
- Let AC be the bisector of ∠PAB and BD be the bisector of ∠RBA.
- According to the problem, it is given that AC∥BD.
3. Use the Property of Parallel Lines:
- Since AC∥BD, by the property of parallel lines, we know that the alternate interior angles formed by these lines are equal.
- Therefore, we can say that ∠PAB=∠RBA.
4. Relate the Angles:
- Since AC is the bisector of ∠PAB, we can express this as:
∠PAC=∠CAB=12∠PAB
- Similarly, since BD is the bisector of ∠RBA:
∠RBA=∠ABD=12∠RBA
5. Set Up the Equation:
- From the previous steps, we have:
∠PAC+∠CAB=∠PAB
∠RBA=∠ABD+∠DAB
- Since AC∥BD, we can conclude that:
∠PAB=∠RBA
6. Conclude the Proof:
- Since ∠PAB and ∠RBA are equal, by the Alternate Interior Angles Theorem, we can conclude that the lines PQ and RS are parallel.
Conclusion:
Thus, we have proved that if the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, then the given lines are parallel.
- Let PQ and RS be two lines cut by a transversal AB.
- Identify the alternate angles formed by the transversal. Let ∠PAB and ∠RBA be the alternate angles.
- Let AC be the bisector of ∠PAB and BD be the bisector of ∠RBA.
- According to the problem, it is given that AC∥BD.
- Since AC∥BD, by the property of parallel lines, we know that the alternate interior angles formed by these lines are equal.
- Therefore, we can say that ∠PAB=∠RBA.
- Since AC is the bisector of ∠PAB, we can express this as:
∠PAC=∠CAB=12∠PAB
- Similarly, since BD is the bisector of ∠RBA:
∠RBA=∠ABD=12∠RBA
- From the previous steps, we have:
∠PAC+∠CAB=∠PAB
∠RBA=∠ABD+∠DAB
- Since AC∥BD, we can conclude that:
∠PAB=∠RBA
- Since ∠PAB and ∠RBA are equal, by the Alternate Interior Angles Theorem, we can conclude that the lines PQ and RS are parallel.
Thus, we have proved that if the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, then the given lines are parallel.
Topper's Solved these Questions
Similar Questions
If the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View SolutionWhich of these pairs of lines are parallel?

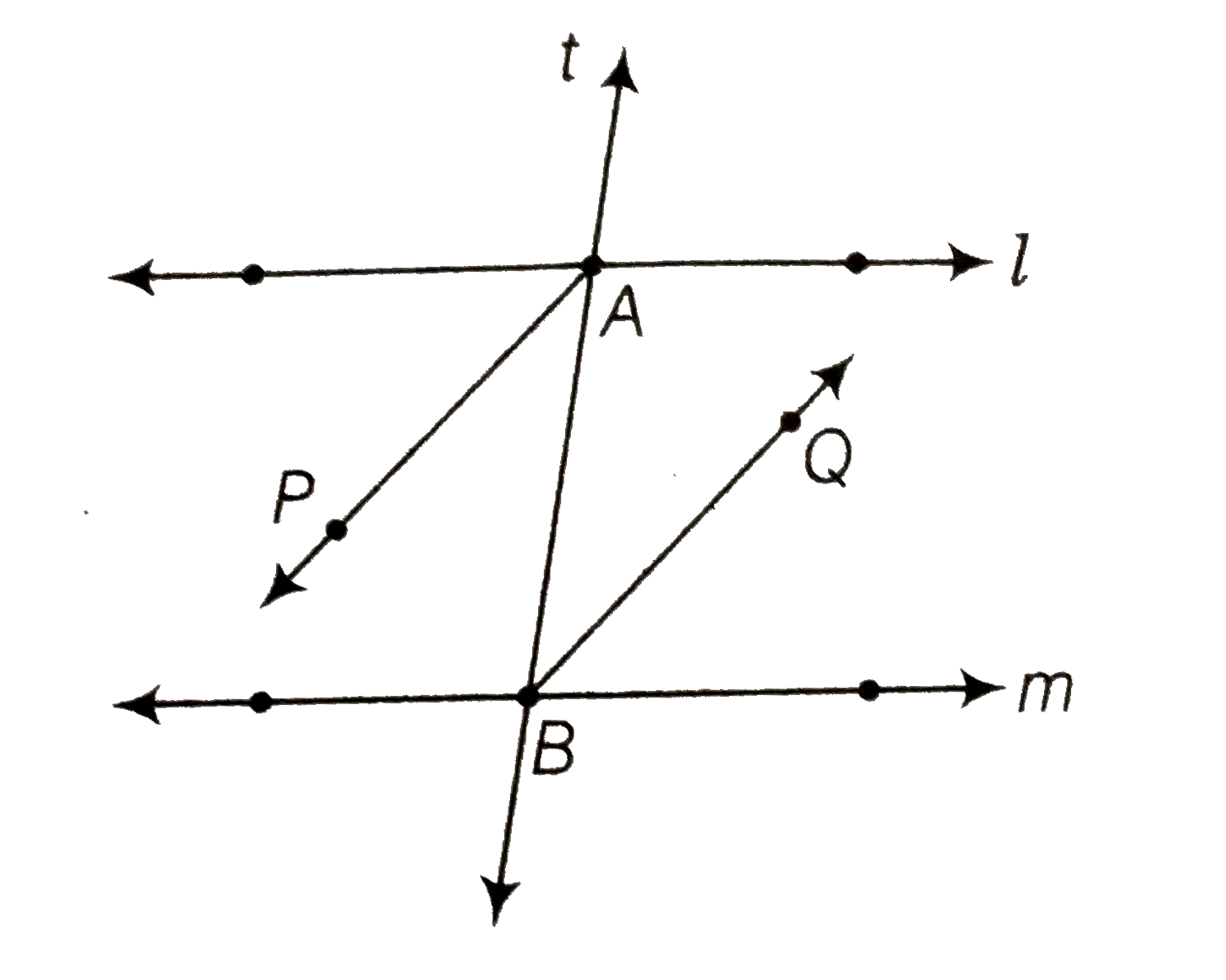
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
View SolutionIf a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
View SolutionProve that the bisectors of a pair of vertically opposite angles are in the same straight line.
View SolutionCan the two lines of regression be parallel?
View SolutionTwo straight lines are cut by a transversal. If the bisectors of a pair of co-interior angles are perpendicular to each other , prove the two straight lines are parallel to each other.
View SolutionTheorem 6.5 : If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
View SolutionProve that two lines perpendicular to the same line are parallel to each other.
View SolutionProve that two lines perpendicular to the same line are parallel to each other.
View Solution
