In Figure , State which lines are parallel and why.
To determine which lines are parallel in the given figure, we will analyze the angles formed by the transversal and the lines.
1. Identify the Lines and Angles:
- We have lines AB and CD, and a transversal AC that intersects these lines.
- The angles formed by this intersection are angle BAC and angle ACD.
2. Recognize Alternate Angles:
- Angle BAC and angle ACD are alternate angles. Alternate angles are formed when a transversal intersects two lines.
3. Measure the Angles:
- According to the information given, angle BAC = angle ACD = 110 degrees.
4. Apply the Alternate Angle Theorem:
- The Alternate Angle Theorem states that if a transversal intersects two lines and the alternate angles are equal, then the lines are parallel.
5. Conclude the Parallel Lines:
- Since angle BAC = angle ACD, we can conclude that lines AB and CD are parallel.
- Therefore, we write: AB || CD (AB is parallel to CD).
Final Answer:
Lines AB and CD are parallel because angle BAC and angle ACD are alternate angles that are equal (both measuring 110 degrees).
---
- We have lines AB and CD, and a transversal AC that intersects these lines.
- The angles formed by this intersection are angle BAC and angle ACD.
- Angle BAC and angle ACD are alternate angles. Alternate angles are formed when a transversal intersects two lines.
- According to the information given, angle BAC = angle ACD = 110 degrees.
- The Alternate Angle Theorem states that if a transversal intersects two lines and the alternate angles are equal, then the lines are parallel.
- Since angle BAC = angle ACD, we can conclude that lines AB and CD are parallel.
- Therefore, we write: AB || CD (AB is parallel to CD).
Lines AB and CD are parallel because angle BAC and angle ACD are alternate angles that are equal (both measuring 110 degrees).
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure below , lines p and q are parallel and angle measures are as marked . If it can be determined , what is the value of a ?
 A35∘B45∘C55∘D100∘
A35∘B45∘C55∘D100∘
In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35∘, what is the measure of ∠2 ?A35∘B55∘C70∘D145∘In the figure, lines l and k are parallel. If a is an acute angle, then which one of the following must be true?
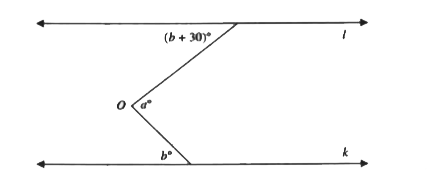 Ab>10Bb>15Cb<20Db<30
Ab>10Bb>15Cb<20Db<30
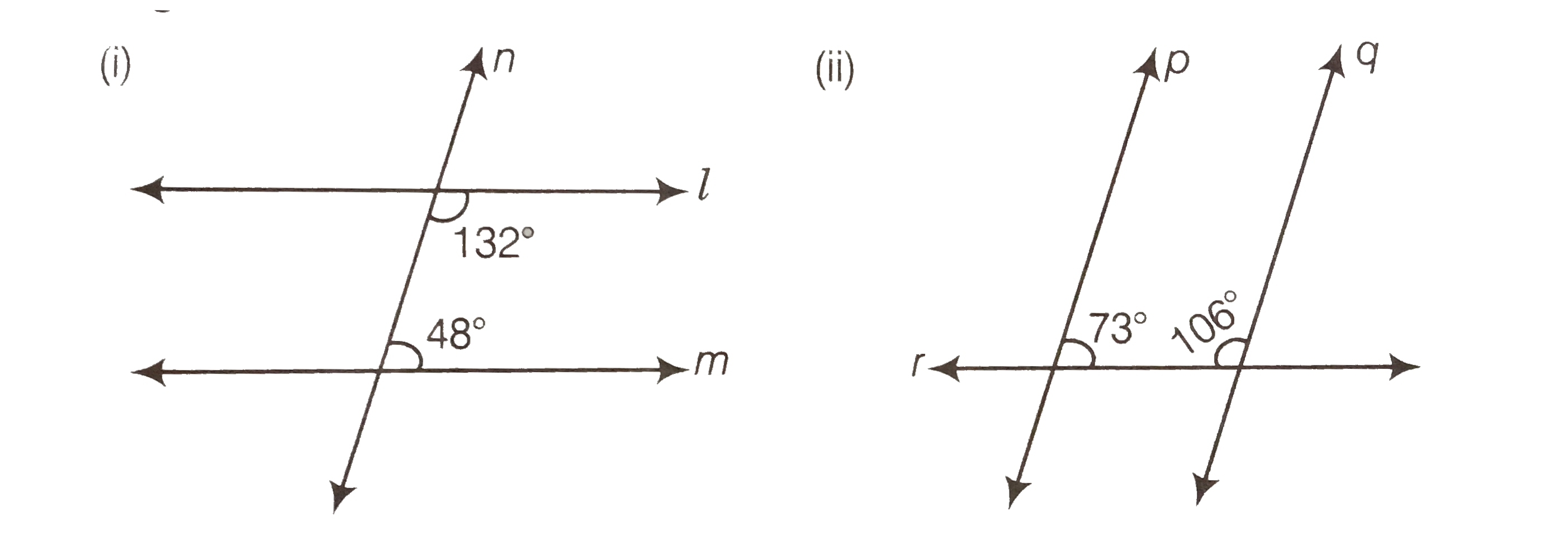
In Figure, if lines l and m are parallel lines, then x=
(a)700
(b) 1000
(c) 400
(d) 300
View SolutionWhich of these pairs of lines are parallel?

View SolutionIn the figure, find the value of x for which the lines l and m are parallel.
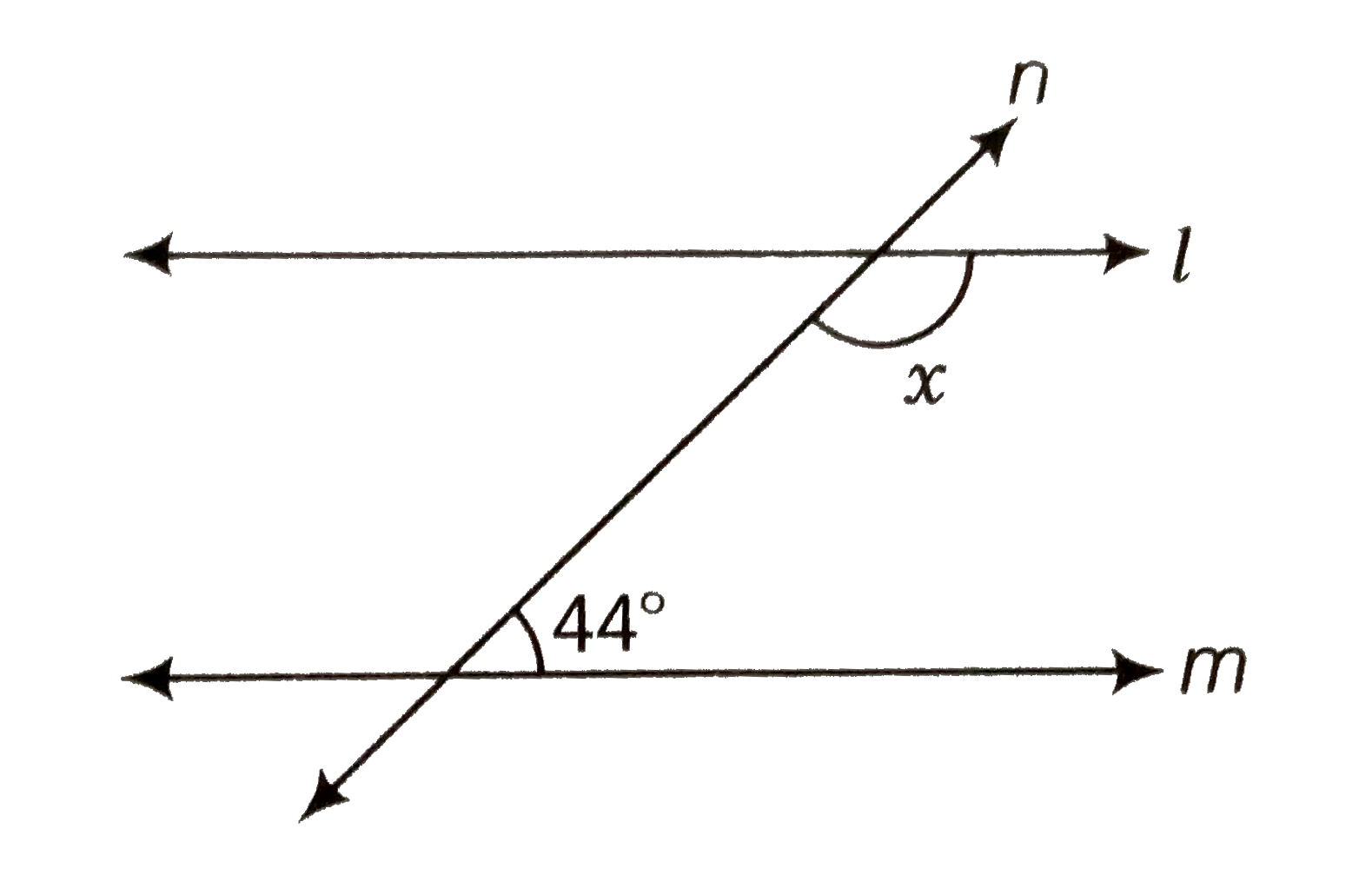
View Solution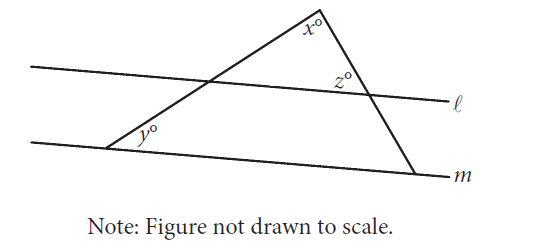
In the figure above, lines l and m are parallel, y = 20, and z = 60. What is the value of x ?
View SolutionIn the figure, lines l and m are parallel. Which of the following. If true, makes lines p and q parallel?

View Solution