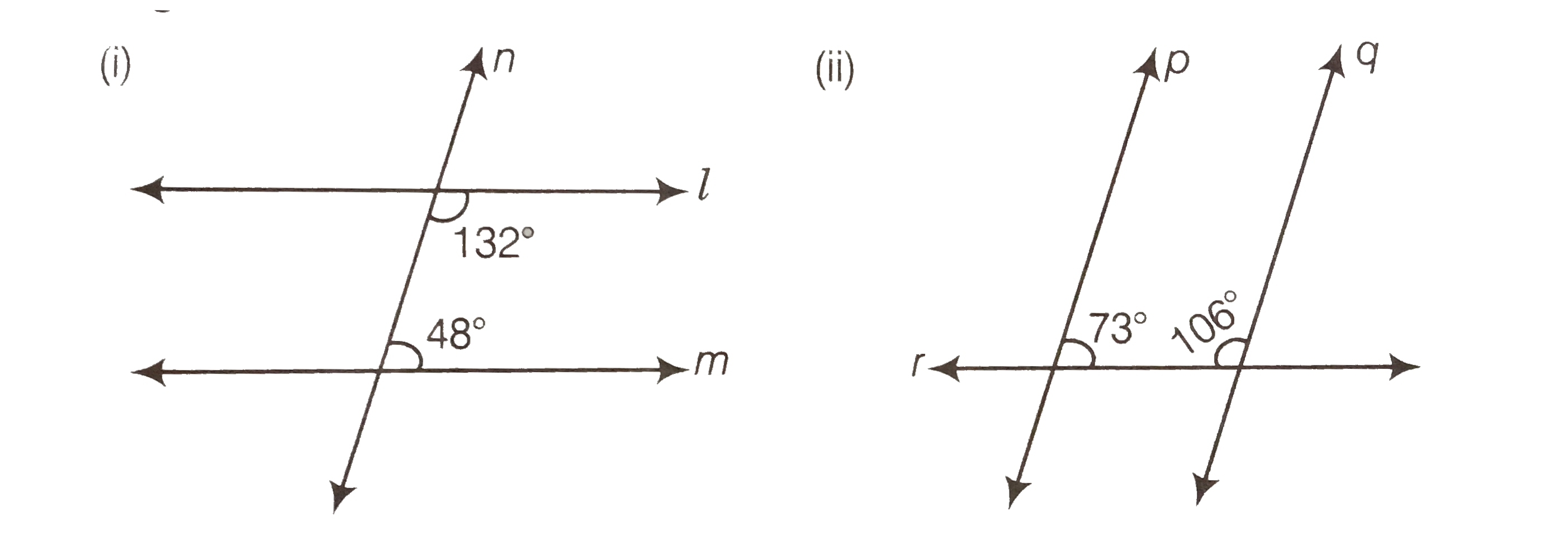
In Fig.86, state which lines are parallel and why?
To determine which lines are parallel in the given figure and provide reasons for the same, we can follow these steps:
1. Identify the Lines and Transversal:
- Let's denote the lines in the figure as follows:
- Line L
- Line M
- Line N
- Line O
- Identify the transversal, which we will denote as line M.
2. Check Lines L and M:
- We need to check if lines L and M are parallel.
- Look at the interior angles formed on the same side of the transversal (line M).
- If the sum of these interior angles is equal to 180 degrees, then lines L and M are parallel.
3. Calculate the Interior Angles:
- Measure the interior angles on the same side of the transversal.
- Suppose the angles are 90 degrees and 88 degrees. Their sum is 178 degrees (90 + 88 = 178).
- Since 178 degrees is not equal to 180 degrees, lines L and M are not parallel.
4. Check Lines N and O:
- Now, we will check lines N and O to see if they are parallel.
- Again, we will use line M as the transversal.
- We need to check the alternate interior angles formed by the transversal.
5. Identify the Alternate Interior Angles:
- Let’s denote the alternate interior angles as angle EDC and angle ACD.
- If angle EDC = angle ACD, then lines N and O are parallel.
6. Measure the Alternate Interior Angles:
- Suppose we find that angle EDC = 100 degrees and angle ACD = 100 degrees.
- Since both angles are equal, we conclude that lines N and O are parallel.
Conclusion:
- Lines L and M are not parallel because the sum of the interior angles on the same side of the transversal is not equal to 180 degrees.
- Lines N and O are parallel because the alternate interior angles are equal.
- Let's denote the lines in the figure as follows:
- Line L
- Line M
- Line N
- Line O
- Identify the transversal, which we will denote as line M.
- We need to check if lines L and M are parallel.
- Look at the interior angles formed on the same side of the transversal (line M).
- If the sum of these interior angles is equal to 180 degrees, then lines L and M are parallel.
- Measure the interior angles on the same side of the transversal.
- Suppose the angles are 90 degrees and 88 degrees. Their sum is 178 degrees (90 + 88 = 178).
- Since 178 degrees is not equal to 180 degrees, lines L and M are not parallel.
- Now, we will check lines N and O to see if they are parallel.
- Again, we will use line M as the transversal.
- We need to check the alternate interior angles formed by the transversal.
- Let’s denote the alternate interior angles as angle EDC and angle ACD.
- If angle EDC = angle ACD, then lines N and O are parallel.
- Suppose we find that angle EDC = 100 degrees and angle ACD = 100 degrees.
- Since both angles are equal, we conclude that lines N and O are parallel.
- Lines L and M are not parallel because the sum of the interior angles on the same side of the transversal is not equal to 180 degrees.
- Lines N and O are parallel because the alternate interior angles are equal.
Topper's Solved these Questions
Similar Questions
In Figure , State which lines are parallel and why.
View SolutionIn the figure, which of the two lines are parallel and why ?
View SolutionIn Fig. state if PQ∣∣EF
View SolutionWhich of these pairs of lines are parallel?

View SolutionExplain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
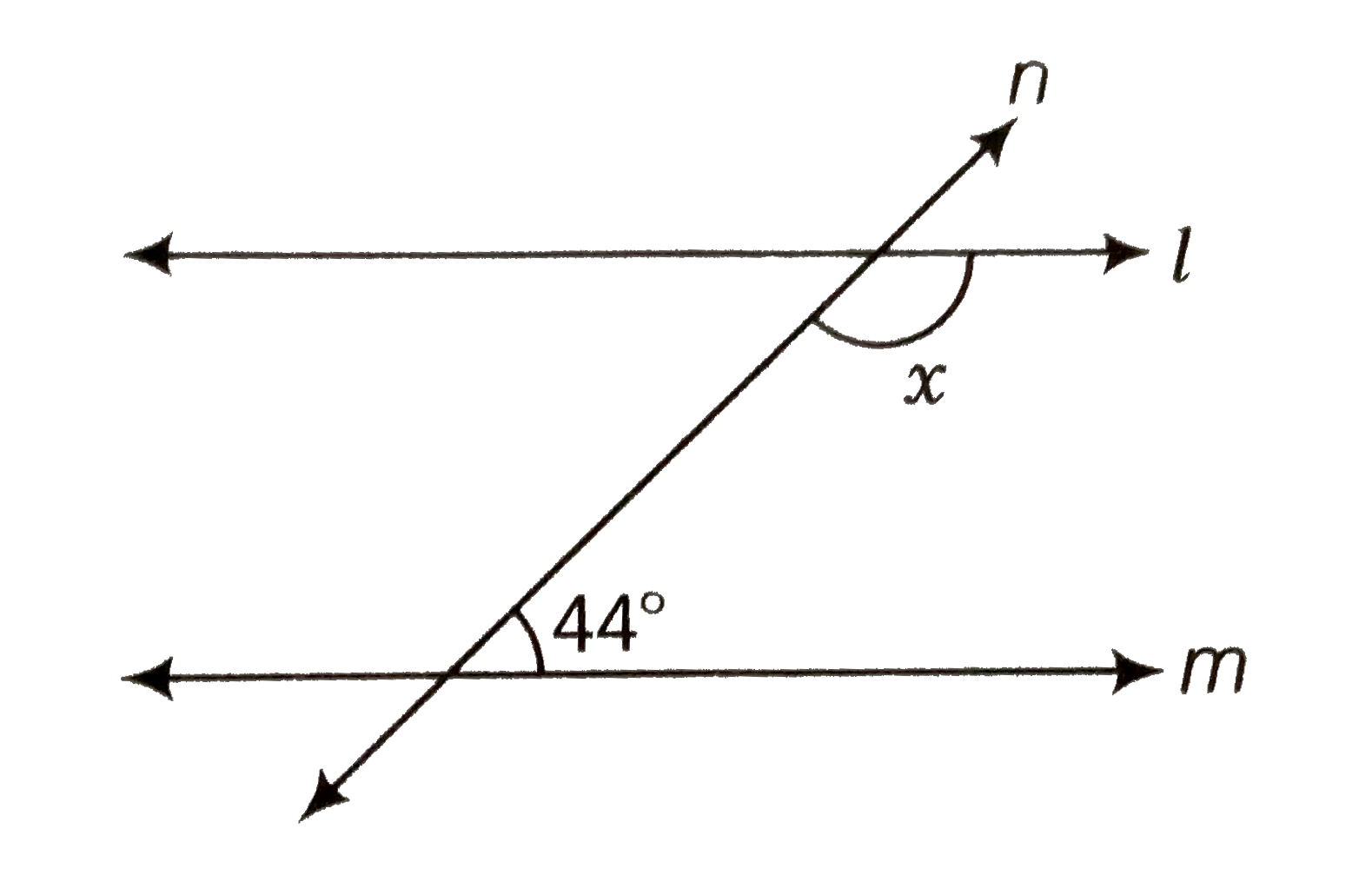
View SolutionIn the figure, find the value of x for which the lines l and m are parallel.
View SolutionBy simply looking at the pair of angles given in Fig., state which of the angles in each of the pairs is greater:
View SolutionIf there are six straight lines in a plane, no two of which are parallel and no three of which pass through the same point, then find the number of points in which these lines intersect.
View SolutionIf the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View Solution