From the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the difference between the heights of the building and the lamp post.
To solve the problem step by step, we will use the properties of right triangles and trigonometric ratios.
1. Identify the given information:
- Height of the building AB=60 m.
- Angle of depression to the top of the lamp post C is 30∘.
- Angle of depression to the bottom of the lamp post D is 60∘.
2. Draw a diagram:
- Draw a vertical line representing the building AB of height 60 m.
- Draw a vertical line for the lamp post CD.
- Mark the angles of depression from point A (top of the building) to points C (top of the lamp post) and D (bottom of the lamp post).
3. Calculate the horizontal distance X from the base of the building to the lamp post:
- In triangle ADB (where D is the bottom of the lamp post):
tan(60∘)=ABX
√3=60X(since tan(60∘)=√3)
X=60√3=20√3 m
4. Calculate the height of the lamp post CD:
- In triangle ACP (where C is the top of the lamp post):
tan(30∘)=60−HX
1√3=60−H20√3
Cross-multiplying gives:
20√3=√3(60−H)
Simplifying:
20=60−H
H=60−20=40 m
5. Find the difference in height between the building and the lamp post:
- The height of the building AB=60 m.
- The height of the lamp post CD=40 m.
- The difference in height is:
AB−CD=60−40=20 m
Final Answer:
The difference between the heights of the building and the lamp post is 20 meters.
- Height of the building AB=60 m.
- Angle of depression to the top of the lamp post C is 30∘.
- Angle of depression to the bottom of the lamp post D is 60∘.
- Draw a vertical line representing the building AB of height 60 m.
- Draw a vertical line for the lamp post CD.
- Mark the angles of depression from point A (top of the building) to points C (top of the lamp post) and D (bottom of the lamp post).
- In triangle ADB (where D is the bottom of the lamp post):
tan(60∘)=ABX
√3=60X(since tan(60∘)=√3)
X=60√3=20√3 m
- In triangle ACP (where C is the top of the lamp post):
tan(30∘)=60−HX
1√3=60−H20√3
Cross-multiplying gives:
20√3=√3(60−H)
Simplifying:
20=60−H
H=60−20=40 m
- The height of the building AB=60 m.
- The height of the lamp post CD=40 m.
- The difference in height is:
AB−CD=60−40=20 m
The difference between the heights of the building and the lamp post is 20 meters.
Topper's Solved these Questions
Similar Questions
From the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the height of the lamp post.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the horizontal distance between AB and CD
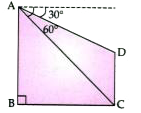
View SolutionIn the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(ii) the height of the lamp post.
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
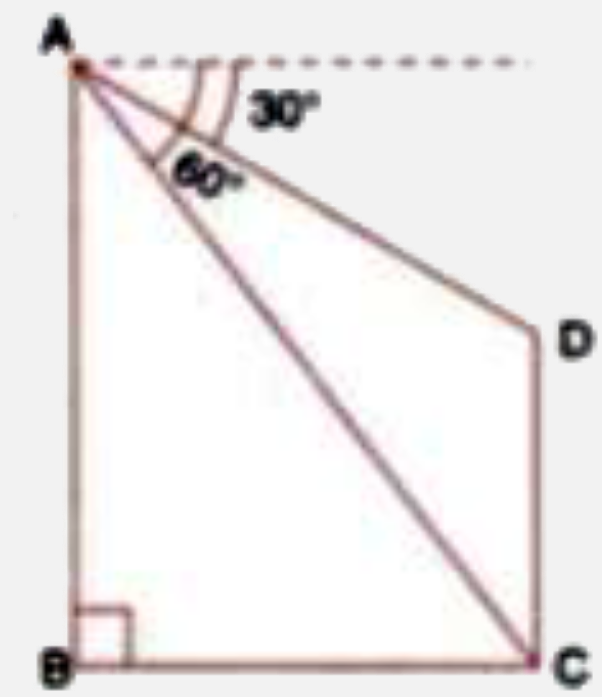
the horizontal distance between AB and CD
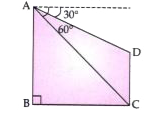
View SolutionIn the igure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(i) the horizontal distance between AB and CD.
View SolutionFrom the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionThe angles of depression of the top and bottom of 8m tall building from the top of a multistoried building are 30o and 45o respectively. Find the height of the multistoried building and the distance between the two buildings.
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
View Solution
